It has almost been a year since I wrote my first leetcode blog post. Today LeetCode starts the 30-Day LeetCoding Challenge. Recently, I am learning golang, and I think praticing LeetCode is a good way to learn a new language, so I will use golang to solve these 30 LeetCode problems.

Week 1: April 1st–April 7th

Single Number

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

Input: [2,2,1]
Output: 1

Example 2:

Input: [4,1,2,1,2]
Output: 4

Explanation

We can use XOR to solve this problem. We know that 0 XOR 0 = 0, 1 XOR 1 = 0, 0 XOR 1 = 1 XOR 0 = 1. For example, we can initialize the res is 0000 first, loop through all the numbers, if the first number is 1010 then res XOR num = 0000 XOR 1010 = 1010. If the second number is also 1010, then res = res XOR num = 1010 XOR 1010 = 0000; If the third number is 1100, then the res = res XOR num = 0000 XOR 1100 = 1100. So we return the third number.

From: [LeetCode] 136. Single Number

Solution

func singleNumber(nums []int) int {
    res := 0
    for _, num := range nums {
        res ^= num
    }
    return res
}

Happy Number

Write an algorithm to determine if a number is “happy”.

A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers.

Example:

Input: 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

Explanation

We can also use two pointer technique to solve this problem. Similar to 141. Linked List Cycle. The difference is in this problem, the cycle must exist. slow will be the sum of the digit square, in other words, slow=calc(slow), fast will be fast=calc(cal(fast)). When slow is equals to fast, we break out the loop, and check if slow is equals to 1. If it’s 1, we return true; else return false.

Solution

func isHappy(n int) bool {
    calc := func(n int) int {
        res := 0
        for n > 0 {
            res += (n % 10) * (n % 10)
            n /= 10
        }
        return res
    }
    slow, fast := n, n
    for {
        if slow == 1 || fast == 1 {
            return true
        }
        slow = calc(slow)
        fast = calc(fast)
        fast = calc(fast)
        if slow == fast {
            break
        }
    }
    return slow == 1
}

Maximum Subarray

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

Explanation 1

We are finding the maximum of a subarray, which means we need to continuosily adding numbers, also we need to return one maximum number, which means we need to have a variable to keep track of the maximum.
While iterating, the sum is keep adding current number. If the sum is less than the current number, we can just drop the sum, and reset the sum to the current number. And we compare the sum with the maximum result.
Finally, return the maximum result.

From: [LeetCode] 53. Maximum Subarray

Solution 1

func maxSubArray(nums []int) int {
    res, curMax := nums[0], nums[0]
    for i := 1; i < len(nums); i++ {
        curMax = findMax(curMax + nums[i], nums[i])
        res = findMax(res, curMax)
    }
    return res
}

func findMax(a, b int) int {
    if (a < b) {
        return b
    } else {
        return a
    }
}

Explanation 2

We can also use divide and conquer method to solve this problem. First, we divide the array into left half and right half, and find their max sum. We also need to find the max sum for the middle part which is crossing the left half and right half, and we can find it by starting from the middle number and scan left side and scan the right side. Finally, compare these three sums.

From: [LeetCode] 53. Maximum Subarray

Solution 2

func maxSubArray(nums []int) int {
    if len(nums) == 0 { return 0 }
    return helper(nums, 0, len(nums)-1)
}

func helper(nums []int, left, right int) int {
    if left == right { return nums[left] }
    mid := left + (right - left) / 2
    leftSum := helper(nums, left, mid)
    rightSum := helper(nums, mid + 1, right)
    midSum := nums[mid]
    temp := midSum
    for i := mid-1; i >= left; i-- {
        temp += nums[i]
        midSum = findMax(midSum, temp)
    }
    temp = midSum
    for i := mid+1; i <= right; i++ {
        temp += nums[i]
        midSum = findMax(midSum, temp)
    }
    return findMax(findMax(leftSum, rightSum), midSum)
}

func findMax(a, b int) int {
    if (a < b) {
        return b
    } else {
        return a
    }
}

Move Zeroes

Given an array nums, write a function to move all 0’s to the end of it while maintaining the relative order of the non-zero elements.

Example:

Input: [0,1,0,3,12]
Output: [1,3,12,0,0]

Note:

You must do this in-place without making a copy of the array.
Minimize the total number of operations.

Explanation

We can use two pointers nonZeroIdx is initalized pointing to the first index, and it is using to points to the first non zero value. i is increasing moving forward. If nums[i] is not zero, then we swap nums[nonZeroIdx] and nums[i] and move nonZeroIdx one step forward. So that next iteration, if nums[i] is not zero again, it will be swapped in front; else if nums[i] is zero, it stays the same position.

Solution

func moveZeroes(nums []int)  {
    nonZeroIdx := 0
    for i := 0; i < len(nums); i++ {
        if nums[i] != 0 {
            nums[nonZeroIdx], nums[i] = nums[i], nums[nonZeroIdx]
            nonZeroIdx += 1
        }
    }
}

Best Time to Buy and Sell Stock II

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
             Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Explanation

Check if the array is empty, if it is, then return 0;
Loop through the array, compare current element with its next element.
- If the next element is greater, then we do noting, just wait for the next element to subtract the minimum element, if reach the end and the next element is still greater, then we sell the minimum using the next element and return the result.
- If the next element is smaller, then we know we need to sell our stock with the current price, and then update the minimum to the next element.
1
2
3
[1, 3, 5, 7, 9, 2] => 9 - 1 = 8 min is the first element 1, we wait for the 9 to subtract it, and update the min to 2.

From: [LeetCode] 122. Best Time to Buy and Sell Stock II

Solution

func maxProfit(prices []int) int {
    if len(prices) == 0 { return 0 }
    profit := 0
    buy := prices[0]
    for i := 0; i < len(prices); i++ {
        if i == len(prices)-1 || prices[i] > prices[i+1] {
            profit += prices[i] - buy
            if i == len(prices)-1 { return profit }
            buy = prices[i+1]
        }
    }
    return profit
}

Group Anagrams

Given an array of strings, group anagrams together.

Example:

Input: ["eat", "tea", "tan", "ate", "nat", "bat"],
Output:
[
  ["ate","eat","tea"],
  ["nat","tan"],
  ["bat"]
]

Note:

All inputs will be in lowercase.
The order of your output does not matter.

Explanation 1

We want to put all same anagrams into a list, so we can sort all strings, then if two sorted strings are equal, then they have the same anagram.
Iterating each string, we can get the string then make it as a char array then do sorting. We put the sorted string into a hashmap<String, List<String>> as key, and the original string as value.
After finish iteration, we can retun the hashmap’s values as a new array list as the result.

From: [LeetCode] 49. Group Anagrams

Solution 1

import (
    "sort"
)
func groupAnagrams(strs []string) [][]string {
    hm := make(map[string][]string)

    for _, str := range strs {
        bytesArr := []byte(str)
        sort.SliceStable(bytesArr, func (i, j int) bool {
            return bytesArr[i] < bytesArr[j]
        })

        sortedStr := string(bytesArr)
        hm[sortedStr] = append(hm[sortedStr], str)
    }

    res := make([][]string, 0)
    for k := range hm {
        res = append(res, hm[k])
    }
    return res
}

Explanation 2

Instead of sorting each string, for each string, we know that if two strings are anagrams, then they will have the same 26 lower case characters frequency. Since the input strings are all lower case, we make an array of size 26 and it’s used to store the frequency of each string. After we storing the frequency to the array, we loop through this frequency array and concat each frequency to a string builder so that we can use it as the key of the hashmap.

Solution 2

func groupAnagrams(strs []string) [][]string {
    getNumRepresent := func(str string) string { return "" }
    getNumRepresent = func(str string) string {
        arr := make([]int, 26)
        for _, r := range str {
            arr[r-'a'] += 1
        }
        var sb strings.Builder
        for _, n := range arr {
            fmt.Fprintf(&sb, "%d", n)
        }
        return sb.String()
    }

    hm := make(map[string][]string)
    for _, str := range strs {
        strNum := getNumRepresent(str)
        hm[strNum] = append(hm[strNum], str)
    }

    res := make([][]string, 0)
    for k := range hm {
        res = append(res, hm[k])
    }
    return res
}

Counting Elements

Given an integer array arr, count element x such that x + 1 is also in arr.

If there’re duplicates in arr, count them seperately.

Example 1:

Input: arr = [1,2,3]
Output: 2
Explanation: 1 and 2 are counted cause 2 and 3 are in arr.

Example 2:

Input: arr = [1,1,3,3,5,5,7,7]
Output: 0
Explanation: No numbers are counted, cause there's no 2, 4, 6, or 8 in arr.

Example 3:

Input: arr = [1,3,2,3,5,0]
Output: 3
Explanation: 0, 1 and 2 are counted cause 1, 2 and 3 are in arr.

Example 4:

Input: arr = [1,1,2,2]
Output: 2
Explanation: Two 1s are counted cause 2 is in arr.

Constraints:

1 <= arr.length <= 1000
0 <= arr[i] <= 1000

Explanation

New Problem! Below are the hints:

Use hashset to store all elements.
Loop again to count all valid elements.

Solution

func countElements(arr []int) int {
    res := 0
    hs := make(map[int]bool)
    for _, num := range arr {
        hs[num] = true
    }
    for _, num := range arr {
        if hs[num+1] {
            res += 1
        }
    }
    return res
}

Week 2: April 8th–April 14th

Middle of the Linked List

Given a non-empty, singly linked list with head node head, return a middle node of linked list.

If there are two middle nodes, return the second middle node.

Example 1:

Input: [1,2,3,4,5]
Output: Node 3 from this list (Serialization: [3,4,5])
The returned node has value 3.  (The judge's serialization of this node is [3,4,5]).
Note that we returned a ListNode object ans, such that:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, and ans.next.next.next = NULL.

Example 2:

Input: [1,2,3,4,5,6]
Output: Node 4 from this list (Serialization: [4,5,6])
Since the list has two middle nodes with values 3 and 4, we return the second one.

Note:

The number of nodes in the given list will be between 1 and 100.

Explanation

We can use slow and fast pointers method to solve this problem.
Fast and slow pointrs are initialized to head. While current fast node and fast.next node is not null, we move fast pointer two steps forward, slow pointer one step forward. Outside the while loop, the slow pointer is the middle node.

Solution

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func middleNode(head *ListNode) *ListNode {
    slow := head
    fast := head
    for fast != nil && fast.Next != nil {
        fast = fast.Next.Next
        slow = slow.Next
    }
    return slow
}

Backspace String Compare

Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character.

Example 1:

Input: S = "ab#c", T = "ad#c"
Output: true
Explanation: Both S and T become "ac".

Example 2:

Input: S = "ab##", T = "c#d#"
Output: true
Explanation: Both S and T become "".

Example 3:

Input: S = "a##c", T = "#a#c"
Output: true
Explanation: Both S and T become "c".

Example 4:

Input: S = "a#c", T = "b"
Output: false
Explanation: S becomes "c" while T becomes "b".

Note:

1 <= S.length <= 200
1 <= T.length <= 200
S and T only contain lowercase letters and '#' characters.

Follow up:

Can you solve it in O(N) time and O(1) space?

Explanation 1

We can solve this problem using stack. For each character, if it’s letter, then we push, else if it’s #, then we pop. At the end, we compare the size of two stacks.

Solution 1

func backspaceCompare(S string, T string) bool {
    return helper(S) == helper(T)
}

func helper(S string) string {
    st := []byte{}
    for i := 0; i < len(S); i++ {
        if S[i] != '#' {
            st = append(st, S[i])
        } else {
            if len(st) == 0 { continue }
            st = st[:len(st)-1]
        }
    }
    return string(st)
}

Explanation 2

We can also solve this problem without stack. We think of it comparing character from right to left. First, we define compare indexes sIdx and tIdx to point to the last character of S and T. While sIdx or tIdx equal or greater than 0, then we pass the string and its compare index to the helper function that will returns index of the rightmost symbol in the string s[:i+1] that’s not deleted by succeeding backspaces. For example if string is abc## and compare index points at the last character, then the updated compare index will be 0. After running the helper function, we compare S[sIdx] with T[tIdx]. Then we decrease both sIdx and tIdx to point to the next preceeding character. Outside the while loop, we return if both sIdx and tIdx are negative.
In the helper function, first we define a variable skip to count how many characters we can remove. While compare index equal or greater than 0, and its pointing character is # or skip > 0, then inside the while loop, if current character is #, we increase skip, else decrease skip. Next, we decrease the compare index to point to the new left character. Outside the while loop, the compare index will be the updated compare index.

Solution 2

func backspaceCompare(S string, T string) bool {
    sIdx, tIdx := len(S)-1, len(T)-1
    for sIdx >= 0 || tIdx >= 0 {
        sIdx = helper(S, sIdx)
        tIdx = helper(T, tIdx)
        if sIdx >= 0 && tIdx >= 0 {
            if S[sIdx] != T[tIdx] { return false }
        } else if sIdx < 0 && tIdx < 0 {
            return true
        } else {
            return false
        }
        sIdx -= 1
        tIdx -= 1
    }
    return sIdx == tIdx
}

func helper(S string, idx int) int {
    skip := 0
    for idx >= 0 && (S[idx] == '#' || skip > 0) {
        if S[idx] == '#' {
            skip += 1
        } else {
            skip -= 1
        }
        idx -= 1
    }
    return idx
}

Min Stack

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

push(x) – Push element x onto stack.
pop() – Removes the element on top of the stack.
top() – Get the top element.
getMin() – Retrieve the minimum element in the stack.

Example:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> Returns -3.
minStack.pop();
minStack.top();      --> Returns 0.
minStack.getMin();   --> Returns -2.

Explanation

We can also use only stack to solve this problem, but now, we also need a variable or pointer called min that equals to the minimum element. Initialilly, min set to the largest integer.
When we push an element, we compare min and the element that get push x. If x is smaller or equal to min, then we first push the min then update the min, then push x. We first push the min because that min represents the previous min. When we later pop element, we don’t want the min goes entirely away, we want min to update to the previous min. Else if the element we are pushing is greater than min, then we just normally push x to the stack.

From: [LeetCode] 155. Min Stack

Solution

type MinStack struct {
    st []int
    min int
}


/** initialize your data structure here. */
func Constructor() MinStack {
    return MinStack{[]int{}, math.MaxInt32}
}


func (this *MinStack) Push(x int)  {
    if x <= this.min {
        this.st = append(this.st, this.min)
        this.min = x
    }
    this.st = append(this.st, x)
}


func (this *MinStack) Pop()  {
    if this.st[len(this.st)-1] == this.min {
        this.st = this.st[:len(this.st)-1]
        this.min = this.st[len(this.st)-1]
    }
    this.st = this.st[:len(this.st)-1]

}


func (this *MinStack) Top() int {
    return this.st[len(this.st)-1]
}


func (this *MinStack) GetMin() int {
    return this.min
}


/**
 * Your MinStack object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Push(x);
 * obj.Pop();
 * param_3 := obj.Top();
 * param_4 := obj.GetMin();
 */

Diameter of Binary Tree

Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

Example:

Given a binary tree

Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].

Note: The length of path between two nodes is represented by the number of edges between them.

Explanation 1

From the above example, the length [4,2,1,3] and [5,2,1,3] both go through the root node. Their totoal length is equals to the left depth [4, 2, 1] plus the right depth [1, 3]. So we can calculate the root’s left depth and right depth, then sum them up. This is one situation of having the longest length. The longest length also can be just go through the root’s left child or just the root’s right child. So we need to compare these 3 cases and return the maximum.
We can also use a HashMap to store the current node and its maximum length. So the key is the TreeNode, the value is its maximum length.

Solution 1

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
var hm = make(map[*TreeNode]int)

func diameterOfBinaryTree(root *TreeNode) int {
    if root == nil { return 0 }
    res := getHeight(root.Left, &hm) + getHeight(root.Right, &hm)
    return max(res, max(diameterOfBinaryTree(root.Left), diameterOfBinaryTree(root.Right)))
}

func getHeight(root *TreeNode, hm *map[*TreeNode]int) int {
    if root == nil { return 0 }
    if _, ok := (*hm)[root]; ok {
        return (*hm)[root]
    }
    (*hm)[root] = 1 + max(getHeight(root.Left, hm), getHeight(root.Right, hm))
    return (*hm)[root]
}

func max(a, b int) int {
    if (a < b) {
        return b
    } else {
        return a
    }
}

Explanation 2

We can also calculate the diameter inside the getHeight function. In the getHeight function, if the root node is null, then we return 0. Then, we recursively calculate the left height and right height. Next, we can calculate the diameter by max(res, leftHeight+rightHeight). Next, we return the height of the root normally.
We can also use a map[TreeNode]int to memorize the height.

Solution 2

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

func diameterOfBinaryTree(root *TreeNode) int {
    res := 0
    hm := make(map[*TreeNode]int)
    getHeight(root, &res, &hm)
    return res
}

func getHeight(root *TreeNode, res *int, hm *map[*TreeNode]int) int {
    if root == nil { return 0 }
    if _, ok := (*hm)[root]; ok {
        return (*hm)[root]
    }
    leftHeight := getHeight(root.Left, res, hm)
    rightHeight := getHeight(root.Right, res, hm)
    *res = max(*res, leftHeight + rightHeight)
    (*hm)[root] = 1 + max(leftHeight, rightHeight)
    return (*hm)[root]
}

func max(a, b int) int {
    if (a < b) {
        return b
    } else {
        return a
    }
}

Last Stone Weight

We have a collection of stones, each stone has a positive integer weight.

Each turn, we choose the two heaviest stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:

If x == y, both stones are totally destroyed;
If x != y, the stone of weight x is totally destroyed, and the stone of weight y has new weight y-x.

At the end, there is at most 1 stone left. Return the weight of this stone (or 0 if there are no stones left.)

Example 1:

Input: [2,7,4,1,8,1]
Output: 1
Explanation:
We combine 7 and 8 to get 1 so the array converts to [2,4,1,1,1] then,
we combine 2 and 4 to get 2 so the array converts to [2,1,1,1] then,
we combine 2 and 1 to get 1 so the array converts to [1,1,1] then,
we combine 1 and 1 to get 0 so the array converts to [1] then that's the value of last stone.

Note:

1 <= stones.length <= 30
1 <= stones[i] <= 1000

Explanation

We can use max heap to solve this problem. First, iterate the input array and add each number into the max heap. While the size of the max heap is equal or greater than 2, then we pop two elements out which is the largest two elements. Then calculate the diff and push the diff back to the max heap. Outside the while loop, we check if the heap has size 1 or 0. If the heap has size 1, we return that element, else return 0.

Solution

func lastStoneWeight(stones []int) int {
    h := &IntHeap{}
    heap.Init(h)

    for _, stone := range stones {
        heap.Push(h, stone)
    }
    for h.Len() >= 2 {
        large := heap.Pop(h).(int)
        small := heap.Pop(h).(int)
        diff := large - small
        if diff != 0 {
            heap.Push(h, diff)
        }
    }

    if h.Len() == 1 {
        return (*h)[0]
    } else {
        return 0
    }
}

// An IntHeap is a max-heap of ints.
type IntHeap []int

func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IntHeap) Push(x interface{}) {
	// Push and Pop use pointer receivers because they modify the slice's length,
	// not just its contents.
	*h = append(*h, x.(int))
}

func (h *IntHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

Contiguous Array

Given a binary array, find the maximum length of a contiguous subarray with equal number of 0 and 1.

Example 1:

Input: [0,1]
Output: 2
Explanation: [0, 1] is the longest contiguous subarray with equal number of 0 and 1.

Example 2:

Input: [0,1,0]
Output: 2
Explanation: [0, 1] (or [1, 0]) is a longest contiguous subarray with equal number of 0 and 1.

Note: The length of the given binary array will not exceed 50,000.

Explanation

When we have any subarray problems, we can think of finding subarray’s accumulate sum to solve the problem. In this problem, if the current element is 0, we subtract 1; if the current element is 1, we plus 1. So if any subarray’s sum is 0, then this subarray will have equal number of 0 and 1.
We will use a hash map to record the key is the sum, the value is the current index. If next time we have the same sum, then we know in between the subarray sum to 0, and this subarray’s length will be the current index i subtract hm.get(sum).
Initially, we will put the entry {0, -1} into the hashmap. For example, if the input array is [0, 1]. When we iterate to number 0, we have sum equals to -1, and we put entry {-1, 0} into the hashmap. Then when we iterate to number 1, we have sum equals to 0. We check the hashmap has key 0, so we get the length by using current index subtract hm.get(0) and we get 1 - (-1) = 2.

Solution

func findMaxLength(nums []int) int {
    res, sum := 0, 0
    hm := make(map[int]int)
    hm[0] = -1

    for i := 0; i < len(nums); i++ {
        if nums[i] == 0 {
            sum -= 1
        } else {
            sum += 1
        }
        if _, ok := hm[sum]; ok {
            res = max(res, i - hm[sum])
        } else {
            hm[sum] = i
        }
    }

    return res
}

func max(a, b int) int {
    if (a < b) {
        return b
    } else {
        return a
    }
}

Perform String Shifts

You are given a string s containing lowercase English letters, and a matrix shift, where shift[i] = [direction, amount]:

direction can be 0 (for left shift) or 1 (for right shift).
amount is the amount by which string s is to be shifted.
A left shift by 1 means remove the first character of s and append it to the end.
Similarly, a right shift by 1 means remove the last character of s and add it to the beginning.

Return the final string after all operations.

Example 1:

Input: s = "abc", shift = [[0,1],[1,2]]
Output: "cab"
Explanation:
[0,1] means shift to left by 1. "abc" -> "bca"
[1,2] means shift to right by 2. "bca" -> "cab"

Example 2:

Input: s = "abcdefg", shift = [[1,1],[1,1],[0,2],[1,3]]
Output: "efgabcd"
Explanation:
[1,1] means shift to right by 1. "abcdefg" -> "gabcdef"
[1,1] means shift to right by 1. "gabcdef" -> "fgabcde"
[0,2] means shift to left by 2. "fgabcde" -> "abcdefg"
[1,3] means shift to right by 3. "abcdefg" -> "efgabcd"

Constraints:

1 <= s.length <= 100
s only contains lower case English letters.
1 <= shift.length <= 100
shift[i].length == 2
0 <= shift[i][0] <= 1
0 <= shift[i][1] <= 100

Explanation

Second new problem! For example, if the string is abc. If left shift 1 time, then we have bca. In other words, s.substring(1) + s.substring(0, 1). If right shift 1 time, then we have cba. In other words, s.substring(3-1) + s.substring(0, 3-1).
First, we need to loop through the shift array. We create a variable start to count the difference of left shift and right shift. If left shift, then we subtract shift[i][1], else we plus shift[i][1].
If start is 0, that means the string is return back to the same position, so we return s.
To avoid out of bound, we module start with the string length. If start is less than 0, that means we left shift the string by abs(start) times. Else if start is greater than 0, that means we right shift start times. Using the above explanation’s example, we can easily return the result.

Solution

func stringShift(s string, shift [][]int) string {
    start := 0
    for _, operation := range shift {
        if operation[0] == 0 {
            start -= operation[1]
        } else {
            start += operation[1]
        }
    }
    if start == 0 { return s }

    start = start % len(s)

    if start < 0 {
        start *= -1
    } else {
        start = len(s) - start
    }

    return s[start:] + s[:start]
}

Week 3: April 15th–April 21st

Product of Array Except Self

Given an array nums of n integers where n > 1, return an array output such that output[i] is equal to the product of all the elements of nums except nums[i].

Example:

Input:  [1,2,3,4]
Output: [24,12,8,6]

Constraint: It’s guaranteed that the product of the elements of any prefix or suffix of the array (including the whole array) fits in a 32 bit integer.

Note: Please solve it without division and in O(n).

Follow up:

Could you solve it with constant space complexity? (The output array does not count as extra space for the purpose of space complexity analysis.)

Explanation 1

In order to calculate the result of one number, res[i], if we know its left side product and right side prodcut, then we can easily calculate res[i] = fwd[i] * bwd[i]. So, we should create two arrays fwd[i] to represent nums[i]’s left side product, bwd[i] to represent nums[i]’s right side product. After we calculate fwd[] and bwd[], then we can calculate res[].

Solution 1

func productExceptSelf(nums []int) []int {
    n := len(nums)
    fwd := make([]int, n)
    bwd := make([]int, n)

    fwd[0] = 1
    for i := 1; i < n; i++ {
        fwd[i] = nums[i-1] * fwd[i-1]
    }

    bwd[n-1] = 1
    for i := n-2; i >= 0; i-- {
        bwd[i] = nums[i+1] * bwd[i+1]
    }

    res := make([]int, n)
    for i := 0; i < n; i++ {
        res[i] = fwd[i] * bwd[i]
    }

    return res
}

Explanation 2

We can also save space by using res[] to replace the fwd[], in other word, we calculate the left side product and save to res[]. Then, we create a variable right initialize to 1 and represent the right side product, then loop from right to left to update res[i] = res[i] * right, and update right = nums[i] * right in each iteration.

Solution 2

func productExceptSelf(nums []int) []int {
    n := len(nums)
    res := make([]int, n)

    res[0] = 1
    for i := 1; i < n; i++ {
        res[i] = nums[i-1] * res[i-1]
    }

    right := 1
    for i := n-1; i >= 0; i-- {
        res[i] = res[i] * right
        right = nums[i] * right
    }

    return res
}

Valid Parenthesis String

Given a string containing only three types of characters: ‘(‘, ‘)’ and ‘*’, write a function to check whether this string is valid. We define the validity of a string by these rules:

Any left parenthesis '(' must have a corresponding right parenthesis ')'.
Any right parenthesis ')' must have a corresponding left parenthesis '('.
Left parenthesis '(' must go before the corresponding right parenthesis ')'.
'*' could be treated as a single right parenthesis ')' or a single left parenthesis '(' or an empty string.
An empty string is also valid.

Example 1:

Input: "()"
Output: True

Example 2:

Input: "(*)"
Output: True

Example 3:

Input: "(*))"
Output: True

Note:

The string size will be in the range [1, 100].

Explanation 1

If there’s no *, then this problem will be very easy. We can solve it by creating a counter cnt. If we have left parenthesis, then cnt += 1; if we have right parenthesis, then cnt -= 1. When cnt is less than 0, we return false. At the end, we check if cnt is equal to 0.
Now, we have the *. If cnt is less than 0, we can use the * to represent the left parenthesis to make it true. So when can we use the * to represent left parenthesis? We have two cases: * ) and * (. In the first case, we can use * to represent the left parenthesis. In the second case, no matter * represent left parenthesis or empty string, it still be false.
We can solve this problem using two stacks: left stack to record the index of the left parenthesis. star stack to record the index of the *. Loop through the string, if the current character is (, we push it to left stack. Else if it’s *, we push it to star stack. Else if the current character is ), then we check if both left stack and star stack are empty, then we return false. If the left stack is not empty, we pop it. Else if the star stack is not empty, we pop it.
After finish looping, we check if both left stack and star stack are empty or not. If they both are empty, we return true. Else, that means we have extra ( or *. While both stacks are not empty, each time, we pop both stacks, and compare the left stack index and star stack index. If the left stack index is greater, that means * is in front the (, so we return false. Outside the while loop, we check if the left stack is empty or not. If left stack is not empty, that means we have extra ( and no * so we return false. Else, we return true.

Solution 1

func checkValidString(s string) bool {
    left := make([]int, 0)
    star := make([]int, 0)

    for i := 0; i < len(s); i++ {
        if s[i] == '(' {
            left = append(left, i)
        } else if s[i] == '*' {
            star = append(star, i)
        } else {
            if len(left) == 0 && len(star) == 0 { return false }
            if len(left) != 0 {
                left = left[:len(left)-1]
            } else if len(star) != 0 {
                star = star[:len(star)-1]
            }
        }
    }

    for len(left) != 0 && len(star) != 0 {
        n, m := len(left), len(star)
        if left[n-1] > star[m-1] { return false }
        left = left[:n-1]
        star = star[:m-1]
    }

    return len(left) == 0
}

Explanation 2:

Since * can be represented as left parenthesis or right parenthesis, we can forward loop one time, and backward loop one time to fnd the solution. In forward loop, we represent * as left parenthesis, in backward loop, we represent * as right parenthesis.
In forward loop, if current character is ( or *, we increase the counter left by 1. If the current character is ), we decrease the counter. When looping, if the counter is less than 0, that means we have more right parenthesis so we return false. After forward looping, if the counter left is equal to 0, we return true. If the counter left is greater than 0, we do not return false yet since we treat all * as left parenthesis but * can actually be represent as empty string.
After forward loop, we can start backward loop. Now, we represent all * as right parenthesis. If current character is ) or *, we increase the counter right by 1, else if the current character is ( then we decrease the right counter by 1. If the counter is less than 0, that means we have more left parenthesis so we return false.
At the end of backward loop, we return true as the result. The reason is now the counter right can either be equal to 0 or greater than 0. If it’s equal to 0, we return true because equal number of left parenthesis and right parenthesis. Why the counter right is greater than 0, but we still return true? The reason is before when we finish the forward loop, we confirm that number of ( plus * are greater than number of ). Now the right is greater than 0 because some right parenthesis are represented by *.

Solution 2:

func checkValidString(s string) bool {
    left, right := 0, 0

    for i := 0; i < len(s); i++ {
        if s[i] == '(' || s[i] == '*' {
            left += 1
        } else {
            left -= 1
        }

        if left < 0 {
            return false
        }
    }

    for i := len(s)-1; i >= 0; i-- {
        if s[i] == ')' || s[i] == '*' {
            right += 1
        } else {
            right -= 1
        }

        if right < 0 {
            return false
        }
    }

    return true
}

Explanation 3:

We can also use brute force recursive way to solve this problem. We create a helper function and pass the string itself, the variable start to represent the current character index, and the counter cnt. Later, if the current character is (, we plus 1. If the current character is ), we subtract 1.
In the helper function, the base case is if cnt is less than 0, we return false. We loop from start to the end of string, if the current character is ( we plus 1, else if it’s ), we subtract 1 and check if cnt is less than 0, then we return false. Else if the current character is *, we recursively check 3 cases: first case is using * as empty string, second case is using * as (, third case is using * as ). If either case is true, we return true. Outside the for loop, we check if cnt is equal to 0.

Solution 3:

func checkValidString(s string) bool {
    return helper(s, 0, 0)
}

func helper(s string, start, cnt int) bool {
    if cnt < 0 { return false }

    for i := start; i < len(s); i++ {
        if s[i] == '(' {
            cnt += 1
        } else if s[i] == ')' {
            cnt -= 1
            if cnt < 0 { return false }
        } else {
            return helper(s, i+1, cnt) || helper(s, i+1, cnt+1) || helper(s, i+1, cnt-1)
        }
    }

    return cnt == 0
}

Explanation 4:

Scan from left to right, and record counts of unpaired ‘(‘ for all possible cases. For ‘(‘ and ‘)’, it is straightforward, just increment and decrement all counts, respectively.

When the character is '*', there are three cases, ‘(‘, empty, or ‘)’, we can think those three cases as three branches in the ongoing route.

Take (**()) as an example. There are 6 chars:

At step 0: only one count = 1.
At step 1: the route will be diverted into three branches, so there are three counts: 1 - 1, 1, 1 + 1 which is 0, 1, 2, for ‘)’, empty and ‘(‘ respectively.
At step 2 each route is diverged into three routes again. so there will be 9 possible routes now.
- For count = 0, it will be diverted into 0 – 1, 0, 0 + 1, which is -1, 0, 1, but when the count is -1, that means there are more ‘)’s than ‘(‘s, and we need to stop early at that route, since it is invalid. we end with 0, 1.
- For count = 1, it will be diverted into 1 – 1, 1, 1 + 1, which is 0, 1, 2
- For count = 2, it will be diverted into 2 – 1, 2, 2 + 1, which is 1, 2, 3

To summarize step 2, we end up with counts of 0,1,2,3

At step 3, increment all counts –> 1,2,3,4

At step 4, decrement all counts –> 0,1,2,3

At step 5, decrement all counts –> -1,0,1,2, the route with count -1 is invalid, so stop early at that route. Now we have 0,1,2.

In the very end, we find that there is a route that can reach count == 0. Which means all ‘(‘ and ‘)’ are cancelled. So, the original String is valid.

Another finding is counts of unpaired ‘(‘ for all valid routes are consecutive integers. So we only need to keep a lower and upper bound of that consecutive integers to save space.

One case doesn’t show up in the example is: if the upper bound is negative, that means all routes have more ‘)’ than ‘(‘ –> all routes are invalid –> stop and return false.

Solution 4:

func checkValidString(s string) bool {
    low, high := 0, 0

    for i := 0; i < len(s); i++ {
        if s[i] == '(' {
            low += 1
            high += 1
        } else if s[i] == ')' {
            if low > 0 {
                low -= 1
            }
            high -= 1
        } else {
            if low > 0 {
                low -= 1
            }
            high += 1
        }

        if high < 0 {
            return false
        }
    }

    return low == 0
}

Source: https://leetcode.com/problems/valid-parenthesis-string/discuss/107577/Short-Java-O(n)-time-O(1)-space-one-pass

Number of Islands

Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Example 1:

Input:
11110
11010
11000
00000

Output: 1

Example 2:

Input:
11000
11000
00100
00011

Output: 3

Explanation 1

We can use DFS and a visited array to solve this problem.
Loop through every element in the two dimensional array, if the element is 1 and it’s not visited, then we start our flood fill dfs helper function to update the visited array. Then, we increase our result counter by 1.
At the end, we return our result.

Solution 1

func numIslands(grid [][]byte) int {
    res := 0
    if grid == nil || len(grid) == 0 { return res }
    row, col := len(grid), len(grid[0])
    visited := make([][]bool, row)
    for i := range visited {
        visited[i] = make([]bool, col)
    }

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if grid[r][c] == '1' && !visited[r][c] {
                res += 1
                dfs(grid, visited, r, c)
            }
        }
    }

    return res
}

func dfs(grid [][]byte, visited [][]bool, r, c int) {
    if r >= 0 && r < len(grid) && c >= 0 && c < len(grid[0]) && grid[r][c] == '1' && !visited[r][c] {
        visited[r][c] = true
        dx := []int{-1, 0, 1, 0}
        dy := []int{0, 1, 0, -1}

        for i := 0; i < 4; i++ {
            newR := r + dy[i]
            newC := c + dx[i]
            dfs(grid, visited, newR, newC)
        }
    }
}

Explanation 2

We can also use BFS to solve this problem. In order to use BFS, we need a queue. We still need to iterate the 2d grid. When the current grid element is 1, we increase the result by 1 and mark its coordinate in the visited 2d array to true. Then, we push the current grid element’s total value (curRow * numOfColumn + curCol) into the queue.
While the queue is not empty, we pop out the total value and use the total value to get back the curRow and curCol. Then we we iterate 4 times, each time we get its updated surrounding position (left, top, right, bottom). If the updated surrounding position is inside the grid and it’s not visited and its value is 1, then we mark the updated position as visited, and then push it to the queue. Repeat until the queue is empty.

Solution 2

func numIslands(grid [][]byte) int {
    res := 0
    if grid == nil || len(grid) == 0 { return res }
    row, col := len(grid), len(grid[0])
    visited := make([][]bool, row)
    queue := make([]int, 0)
    for i := range visited {
        visited[i] = make([]bool, col)
    }

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if grid[r][c] == '1' && !visited[r][c] {
                res += 1
                queue = append(queue, r * col + c)
                for len(queue) > 0 {
                    pop := queue[0]
                    pR := pop / col
                    pC := pop % col
                    queue = queue[1:]
                    dx := []int{-1, 0, 1, 0}
                    dy := []int{0, 1, 0, -1}
                    for i := 0; i < 4; i++ {
                        newR := pR + dy[i]
                        newC := pC + dx[i]
                        if newR >= 0 && newR < row && newC >= 0 && newC < col && grid[newR][newC] == '1' && !visited[newR][newC] {
                            queue = append(queue, newR * col + newC)
                            visited[newR][newC] = true
                        }
                    }
                }
            }
        }
    }

    return res
}

Explanation 3

This is a disjoin set or union find problem.
First, we creat an array parent[] that has size row * col, and a variable cnt. Loop through every element, if the current element is 1, then we increase cnt and update parent[i] = i.
Next, we loop through every element again, this time if the current element is 1, then we check its 4 neighbor directions. If its neighbor is not out of bound and its element is also 1, then we find the current element’s parent and its neighbor’s parent. If both parent is not the same, we union both parents and subract cnt by 1.
At the end, we return cnt as the result.

Solution 3

func numIslands(grid [][]byte) int {
    res := 0
    if grid == nil || len(grid) == 0 { return res }
    row, col := len(grid), len(grid[0])
    parent := make([]int, row * col)

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if grid[r][c] == '1' {
                parent[r * col + c] = r * col + c
                res += 1
            }
        }
    }

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if grid[r][c] == '1' {
                dx := []int {-1, 0, 1, 0}
                dy := []int {0, 1, 0, -1}
                for i := 0; i < 4; i++ {
                    newR := r + dy[i]
                    newC := c + dx[i]
                    if newR >= 0 && newR < row && newC >= 0 && newC < col && grid[newR][newC] == '1' {
                        curParent := findParent(parent, r * col + c)
                        dirParent := findParent(parent, newR * col + newC)
                        if curParent != dirParent {
                            parent[curParent] = dirParent
                            res -= 1
                        }
                    }
                }
            }
        }
    }

    return res
}

func findParent(parent []int, p int) int {
    for p != parent[p] {
        p = parent[parent[p]]
    }
    return p
}

From: [LeetCode] 200. Number of Islands

Minimum Path Sum

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

Input:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

Explanation 1

Similar to 62. Unique Paths, we can create a dp[][] and use dynamic programming to solve this problem.
The base case is dp[0][0] has the same value as grid[0][0]. The top row element will be its current value plus its left value, dp[0][col] = grid[0][col] + dp[0][col-1]. The left most column element will be its current value plus its top value, dp[row][0] = grid[row][0] + dp[row-1][0].
Now, we need to find the function. The function to calculate dp[row][col] will be its current value plus the minimum between its top value and its left value. In other word, dp[row][col] = grid[row][col] + min(dp[row-1][col], dp[row][col-1]).
The result will be the bottom right element of dp, which is dp[row-1][col-1].

Solution 1

func minPathSum(grid [][]int) int {
    row, col := len(grid), len(grid[0])
    pathSum := make([][]int, row)
    for i := range pathSum {
        pathSum[i] = make([]int, col)
    }
    pathSum[0][0] = grid[0][0]
    for r := 1; r < row; r++ {
        pathSum[r][0] = pathSum[r-1][0] + grid[r][0]
    }
    for c := 1; c < col; c++ {
        pathSum[0][c] = pathSum[0][c-1] + grid[0][c]
    }
    for r := 1; r < row; r++ {
        for c := 1; c < col; c++ {
            pathSum[r][c] = min(pathSum[r-1][c], pathSum[r][c-1]) + grid[r][c]
        }
    }
    return pathSum[row-1][col-1]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Explanation 2

We can save by space by using a 1 dimensional array dp[] that has size col. Initialize all its elements as INT_MAX except dp[0] = 0. The reason we can use the 1 dimensional array is the current element’s min sum is only depends on its left and top element’s min sum.
We don’t need to calculate the min sum of the first row and first column. Instead, when we iterate, if c == 0 that means its first column, so we can update dp[c] = grid[r][c] + dp[c]. Else, we need to compare the left element’s dp[c-1] and top element’s dp[c] and choose the minimum one. If the current element is on the first row, dp[c] is the INT_MAX, so we will choose the minimum dp[c-1] which is on the left side, then plus the current element grid[r][c], so dp[c] = grid[r][c] + min(dp[c], dp[c-1]).

Solution 2

func minPathSum(grid [][]int) int {
    row, col := len(grid), len(grid[0])
    dp := make([]int, col)
    for i := range dp {
        dp[i] = math.MaxInt32
    }
    dp[0] = 0
    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if c == 0 {
                dp[c] = grid[r][c] + dp[c]
            } else {
                dp[c] = grid[r][c] + min(dp[c], dp[c-1])
            }
        }
    }
    return dp[col-1]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Explanation 3

We can also save space by replacing the grid element. We need to iterate every element. If the current element is grid[0][0], then we continue. Else if r == 0, then we update the current element plus its left element. Else if c == 0, then we update the current element plus its top element. Else, we update the current element plus the minimum of its left and top element.

Solution 3

func minPathSum(grid [][]int) int {
    row, col := len(grid), len(grid[0])
    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if r == 0 && c == 0 {
                continue
            } else if r == 0 {
                grid[r][c] += grid[r][c-1]
            } else if c == 0 {
                grid[r][c] += grid[r-1][c]
            } else {
                grid[r][c] += min(grid[r][c-1], grid[r-1][c])
            }
        }
    }
    return grid[row-1][col-1]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

From: [LeetCode] 64. Minimum Path Sum

Search in Rotated Sorted Array

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

Your algorithm’s runtime complexity must be in the order of O(log n).

Example 1:

Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4

Example 2:

Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1

Explanation

For example, the array is [3, 4, 5, 6, 7, 8, 9, 1, 2], the middle element is 7. We can draw the graph like below:

                   /
                 /
               /(mid)
             /
           /
         /
       /(left = 3)
                      /(right = 2)
                     /

We need to consider two cases, case1, the mid is greater than left, case2 is the mid is less than left. The above example is case1. In case1, if the target is greater than left and target is less than mid, then we can set right = mid, else, we set left = mid. Then, we recusivly find the mid and check again. In case2, if target is less than right and target is greater than mid, then we can set left = mid, else, we set right = mid. Then, we also recursivly find the mid and check again.
When the left and right is next to each other, we can break out the loop, and check left and right individually. If not found the target, we return -1.

From: [LeetCode] 33. Search in Rotated Sorted Array

Solution

func search(nums []int, target int) int {
    left, right := 0, len(nums)-1
    for left <= right {
        mid := left + (right - left) / 2
        if nums[mid] == target { return mid }
        if nums[mid] >= nums[left] {
            if nums[left] <= target && target <= nums[mid] {
                right = mid
            } else {
                left = mid + 1
            }
        } else {
            if nums[mid] <= target && target <= nums[right] {
                left = mid + 1
            } else {
                right = mid
            }
        }
    }
    return -1
}

Construct Binary Search Tree from Preorder Traversal

Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

Example 1:

Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

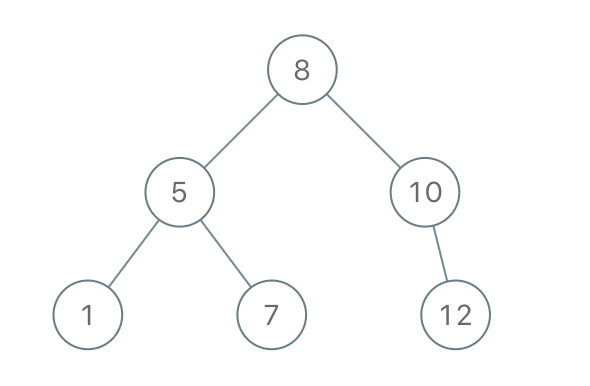
Note:

1 <= preorder.length <= 100
The values of preorder are distinct.

Explanation 1

Since the input array is preorder traversal, so the first element is the root. From the problem’s example, 8 will be the root. How do we knowroot.left and root.right? root.left = 5 because 5 is the next element of 8, and 5 is less than 8. To find root.right, we need to loop from the second element to the right until the current element is greater than the root, which is 10 from the above example.
Now we know [5, 1, 7] will be in the left subtree, [10, 12] will be in the right subtree. We can create a helper method, pass the input array, and two variables start and end which represent the range of the subarray. This helper method will recursively create the binary search tree for the left subtree and right subtree.

Solution 1

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstFromPreorder(preorder []int) *TreeNode {
    if preorder == nil || len(preorder) == 0 { return nil }
    return helper(preorder, 0 , len(preorder)-1)
}

func helper(preorder []int, start int, end int) *TreeNode {
    if start > end { return nil }
    root := &TreeNode{ Val: preorder[start] }
    if start == end { return root }
    i := start + 1
    for i <= end && preorder[i] < preorder[start] {
        i += 1
    }
    root.Left = helper(preorder, start+1, i-1)
    root.Right = helper(preorder, i, end)
    return root
}

Explanation 2

We can also solve this problem in $O(n)$ runtime by using a global index i to represent the current index of the input array. Reading the problem, 5 is the left child or 8, 1 is the left child of 5, …, 7 cannot be the left child of 1 since 7 > 1, and 7 cannot be the right child of 1 since 7 > 5, but 7 can be the right child of 5 since 7 < 8.
We can create a helper method, pass in the input array and the upper bound variablebound which initialize to INT_MAX. In the helper method, we create the root node, root.left will have the upper bound of root.val, and root.right will have the upper bound of bound. The base case is if i == len(preorder) or preorder[i] > bound, then we return NULL.

Solution 2

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstFromPreorder(preorder []int) *TreeNode {
    if preorder == nil || len(preorder) == 0 { return nil }
    i := 0
    return helper(preorder, math.MaxInt32, &i)
}

func helper(preorder []int, bound int, i *int) *TreeNode {
    if *i == len(preorder) || preorder[*i] > bound { return nil }
    root := &TreeNode{Val: preorder[*i]}
    *i += 1
    root.Left = helper(preorder, root.Val, i)
    root.Right = helper(preorder, bound, i)
    return root
}

Leftmost Column with at Least a One

(This problem is an interactive problem.)

A binary matrix means that all elements are 0 or 1. For each individual row of the matrix, this row is sorted in non-decreasing order.

Given a row-sorted binary matrix binaryMatrix, return leftmost column index(0-indexed) with at least a 1 in it. If such index doesn’t exist, return -1.

You can’t access the Binary Matrix directly. You may only access the matrix using a BinaryMatrix interface:

BinaryMatrix.get(x, y) returns the element of the matrix at index (x, y) (0-indexed).
BinaryMatrix.dimensions() returns a list of 2 elements [m, n], which means the matrix is m * n.

Submissions making more than 1000 calls to BinaryMatrix.get will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.

For custom testing purposes you’re given the binary matrix mat as input in the following four examples. You will not have access the binary matrix directly.

Example 1:

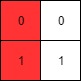
Input: mat = [[0,0],[1,1]]
Output: 0

Example 2:

Input: mat = [[0,0],[0,1]]
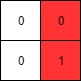
Output: 1

Example 3:

Input: mat = [[0,0],[0,0]]
Output: -1

Example 4:

Input: mat = [[0,0,0,1],[0,0,1,1],[0,1,1,1]]
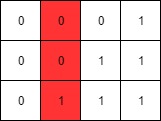
Output: 1

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 100
mat[i][j] is either 0 or 1.
mat[i] is sorted in a non-decreasing way.

Explanation 1

New Problem!
(Binary Search) For each row do a binary search to find the leftmost one on that row and update the answer.

Solution 1

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * type BinaryMatrix struct {
 *     Get(int, int) int
 *     Dimensions() []int
 * }
 */

func leftMostColumnWithOne(binaryMatrix BinaryMatrix) int {
    res := math.MaxInt32
    row, col := binaryMatrix.Dimensions()[0], binaryMatrix.Dimensions()[1]

    for r := 0; r < row; r++ {
        left, right := 0, col - 1
        for left < right {
            mid := left + (right - left) / 2
            if binaryMatrix.Get(r, mid) == 0 {
                left = mid + 1
            } else {
                right = mid
            }
        }
        if binaryMatrix.Get(r, left) == 1 {
            res = min(res, left)
        }
        if res == 0 {
            return res
        }
    }

    if res == math.MaxInt32 {
        return -1
    } else {
        return res
    }
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Explanation 2

(Optimal Approach) Imagine there is a pointer p(x, y) starting from top right corner. p can only move left or down. If the value at p is 0, move down. If the value at p is 1, move left. Try to figure out the correctness and time complexity of this algorithm.

Solution 2

/**
 * // This is the BinaryMatrix's API interface.
 * // You should not implement it, or speculate about its implementation
 * type BinaryMatrix struct {
 *     Get(int, int) int
 *     Dimensions() []int
 * }
 */

func leftMostColumnWithOne(binaryMatrix BinaryMatrix) int {
    res := math.MaxInt32
    row, col := binaryMatrix.Dimensions()[0], binaryMatrix.Dimensions()[1]
    r, c := 0, col - 1

    for r < row && c >= 0 {
        if binaryMatrix.Get(r, c) == 0 {
            r += 1
        } else {
            res = min(res, c)
            c -= 1
        }
    }

    if res == math.MaxInt32 {
        return -1
    } else {
        return res
    }
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Week 4: April 22nd–April 28th

Subarray Sum Equals K

Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.

Example 1:

Input:nums = [1,1,1], k = 2
Output: 2

Note:

The length of the array is in range [1, 20,000].
The range of numbers in the array is [-1000, 1000] and the range of the integer k is [-1e7, 1e7].

Hint 1:

Will Brute force work here? Try to optimize it.

Hint 2:

Can we optimize it by using some extra space?

Hint 3:

What about storing sum frequencies in a hash table? Will it be useful?

Hint 4:

sum(i,j)=sum(0,j)-sum(0,i), where sum(i,j) represents the sum of all the elements from index i to j-1. Can we use this property to optimize it.

Explanation 1

First, we create an accumulation sum array sums by coping the input array, then iterate it, each iteration, we update sums[i] = sums[i-1] + nums[i].
Next, we check all the accumulation sum array and compare with k. We iterate this accumulation sum array. First check if sums[i] == k, if it’s true, we increase the result. Then, we think of i as the ending index of the subarray, loop j from 0 to i-1 inclusive. We check every accumulate sum array sums[i] - sums[j] if it’s equals to k.

Solution 1

func subarraySum(nums []int, k int) int {
    res := 0
    sums := make([]int, len(nums))
    sums[0] = nums[0]
    for i := 1; i < len(nums); i++ {
        sums[i] = sums[i-1] + nums[i]
    }
    for i := 0; i < len(sums); i++ {
        if sums[i] == k {
            res += 1
        }
        for j := 0; j < i; j++ {
            if sums[i] - sums[j] == k {
                res += 1
            }
        }
    }
    return res
}

Explanation 2

Brute force solution. Two loop, loop i as the starting index of the subarray, j as the last index of the subarray, nums[i, j] and check if all elements inside this array sum to k.

Solution 2

func subarraySum(nums []int, k int) int {
    res := 0
    for i := 0; i < len(nums); i++ {
        sum := nums[i]
        if sum == k {
            res += 1
        }
        for j := i+1; j < len(nums); j++ {
            sum += nums[j]
            if sum == k {
                res += 1
            }
        }
    }
    return res
}

Explanation 3

Hashmap<sum[0, i - 1], frequency>.

     sum[i, j] = sum[0, j] - sum[0, i - 1]    --> sum[0, i - 1] = sum[0, j] - sum[i, j]
     k           sum      hashmapKey          -->  hashmapKey   =  sum - k

Now, we have k and sum. As long as we can find a sum[0, i - 1], we then get a valid subarray which is as long as we have the hashmapKey, we then get a valid subarray.
Initially, hm[0] = 1 because if k = 7, we have array [2, -2, 3, -3, 7], the answer should be 3. When we iterate to element 7, we have hm[0] = 2. Since [7] is also one possible answer and hm[sum - k = 7 - 7 = 0], so we initialize hm[0] = 1.

Solution 3

func subarraySum(nums []int, k int) int {
    res := 0
    sum := 0
    hm := make(map[int]int)
    hm[0] = 1
    for i := 0; i < len(nums); i++ {
        sum += nums[i]
        if freq, ok := hm[sum - k]; ok {
            res += freq
        }
        hm[sum] += 1
    }
    return res
}

Bitwise AND of Numbers Range

Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive.

Example 1:

Input: [5,7]
Output: 4

Example 2:

Input: [0,1]
Output: 0

Explanation

We know that all the numbers in the array are consecutive, so their right most part must be different. For example, 101 and 110 are consecutive numbers, and their right most 2 bit are different. Therefore, we only need to find their same left most bit, in this case is 1. And after 1, there are two bits, so the result is 100, which is 4.
We can achieve this by right shift m and n, until they are the same, in other word, we get the common left most bit. While we shifting, we record how many bits we shift. At the end, we shift the same bit to the left to get the result.

Solution

func rangeBitwiseAnd(m int, n int) int {
    cnt := 0
    for m != n {
        m >>= 1
        n >>= 1
        cnt += 1
    }
    return m << cnt
}

LRU Cache

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1.

put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

The cache is initialized with a positive capacity.

Follow up:

Could you do both operations in O(1) time complexity?

Example:

LRUCache cache = new LRUCache( 2 /* capacity */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

Explanation

We can use doubly linked list storing class node to achieve adding and removing in $O(1)$ time by using prev and next pointer. When we do get, we can use hashmap to achieve getting the value by key in $O(1)$ time.
Besides put and get function, we also need to have remove and setHead function. If we run get on a node, then that node need to set it as head. If we have number of capacity node in our linked list, then if we put one more node, we need to remove the tail node.

From: [LeetCode] 146. LRU Cache

Solution

type Node struct {
    Key int
    Value int
    Prev *Node
    Next *Node
}

type LRUCache struct {
    Cap int
    Hm map[int]*Node
    Head *Node
    Tail *Node
}


func Constructor(capacity int) LRUCache {
    cache := LRUCache{}
    cache.Cap = capacity
    cache.Hm = make(map[int]*Node)

    return cache
}


func (this *LRUCache) Get(key int) int {
    if valNode, ok := this.Hm[key]; ok {
        this.remove(valNode)
        this.setHead(valNode)
        return valNode.Value
    } else {
        return -1
    }
}


func (this *LRUCache) Put(key int, value int)  {
    if valNode, ok := this.Hm[key]; ok {
        this.remove(valNode)
        valNode.Value = value
        this.setHead(valNode)
    } else {
        if len(this.Hm) >= this.Cap {
            delete(this.Hm, this.Tail.Key)
            this.remove(this.Tail)
        }
        tempNode := &Node{Key: key, Value: value}
        this.Hm[key] = tempNode
        this.setHead(tempNode)
    }
}

func (this *LRUCache) remove(n *Node) {
    if n.Prev != nil {
        n.Prev.Next = n.Next
    } else {
        this.Head = n.Next
    }

    if n.Next != nil {
        n.Next.Prev = n.Prev
    } else {
        this.Tail = n.Prev
    }
}

func (this *LRUCache) setHead(n *Node) {
    if this.Head != nil {
        this.Head.Prev = n
    }
    n.Next = this.Head
    n.Prev = nil
    this.Head = n

    if this.Tail == nil {
        this.Tail = this.Head
    }
}


/**
 * Your LRUCache object will be instantiated and called as such:
 * obj := Constructor(capacity);
 * param_1 := obj.Get(key);
 * obj.Put(key,value);
 */

Jump Game

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

Example 1:

Input: [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

Input: [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum
             jump length is 0, which makes it impossible to reach the last index.

Explanation

First we create a variable max = 0 to record the maximum position we can reach. Then we iterate the array, update max = max(max, i+nums[i]), if max >= nums[len(nums)-1], we return true. Else if i > max, we break out the loop and return false.

From: [LeetCode] 55. Jump Game

Solution

func canJump(nums []int) bool {
    max := 0
    for i := 0; i < len(nums) && i <= max; i++ {
        max = getMax(max, nums[i] + i)
        if max >= len(nums) - 1 {
            return true
        }
    }
    return false
}

func getMax(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Longest Common Subsequence

Given two strings text1 and text2, return the length of their longest common subsequence.

A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, “ace” is a subsequence of “abcde” while “aec” is not). A common subsequence of two strings is a subsequence that is common to both strings.

If there is no common subsequence, return 0.

Example 1:

Input: text1 = "abcde", text2 = "ace"
Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

1 <= text1.length <= 1000
1 <= text2.length <= 1000

The input strings consist of lowercase English characters only.

Explanation

We can use dynamic programming to solve this problem. Dynamic init is creating a two dimensional array dp[r][c] which represents the length of the longest common subsequence (LCS) for text1[0 : r] and text2[0 : c].
Dynamic base is for text1 or text2 that have length 0, then their length of LCS is 0, in other words, for the dp[r][c], the top row and the left most column will be 0.
Dynamic function. If the rth index for text1 and the cth index for text2 are the same text1[r-1] == text2[c-1], then dp[r][c] = 1 + dp[r-1][c-1]. Else, dp[r][c] = max(dp[r-1][c], dp[r][c-1]).
Dynamic result is the last index for both text1 and text2 in dp which is dp[len(text1), len(text2)].

Solution

func longestCommonSubsequence(text1 string, text2 string) int {
    dp := make([][]int, len(text1) + 1)
    for i := range dp {
        dp[i] = make([]int, len(text2) + 1)
    }

    for r := 0; r < len(dp); r++ {
        for c := 0; c < len(dp[0]); c++ {
            if r == 0 || c == 0 {
                dp[r][c] = 0
            } else {
                if text1[r-1] == text2[c-1] {
                    dp[r][c] = 1 + dp[r-1][c-1]
                } else {
                    dp[r][c] = max(dp[r-1][c], dp[r][c-1])
                }
            }
        }
    }

    return dp[len(text1)][len(text2)]
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Maximal Square

Given a 2D binary matrix filled with 0’s and 1’s, find the largest square containing only 1’s and return its area.

Example:

Input:

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Output: 4

Explanation 1

We can solve this problemm using dynamic programming. For each matrix element except the first row and first column, we think of it as the bottom right point of the square. Also, we will use an extra $m x n$ two dimensional array dp to keep track of the max length of the square base on that iterative matrix point. This iterative point, or bottom right point of the square, its maximum square’s length dp[r][c] will depends on its left point dp[r][c-1], top point dp[r-1][c], and top left point dp[r-1][c-1]. In other words, dp[r][c] will be the minimum of its left point level, top point level, and top left point level. But if this iterative matrix point is 0, then its level will be 0, we don’t need to check its left, top, and top left. For every iteration, we keep track of the maximum level or length. When we iterative to the bottom right, we have calculated all the length base on every points. At the end, we will return the square of the maximum length as the result.
Dynamic init and base is first row and first column don’t change, in other word, dp[0][c] = matrix[0][c], dp[r][0] = matrix[r][0].
Dynamic function is dp[r][c] = min (dp[r-1][c], dp[r][c-1], dp[r-1][c-1]) + 1 only if matrix[r][c] != 0. If matrix[r][c] = 0, then dp[r][c] = 0.
Dynmaic result is the square of maximum level.

Solution 1

func maximalSquare(matrix [][]byte) int {
    if matrix == nil || len(matrix) == 0 || len(matrix[0]) == 0 {
        return 0
    }
    row := len(matrix)
    col := len(matrix[0])
    dp := make([][]int, row)
    for i := range dp {
        dp[i] = make([]int, col)
    }
    maxSideLength := 0

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if r == 0 || c == 0 {
                dp[r][c] = int(matrix[r][c] - '0')
            } else {
                if matrix[r][c] == '0' {
                    dp[r][c] = 0
                } else {
                    left := dp[r][c-1]
                    top := dp[r-1][c]
                    topLeft := dp[r-1][c-1]
                    dp[r][c] = min(topLeft, min(top, left)) + 1
                }
            }
            maxSideLength = max(maxSideLength, dp[r][c])
        }
    }

    return maxSideLength * maxSideLength
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Explanation 2

We can save space by using an one dimensional array dp[r+1], which has length row + 1. This time, we loop from top to bottom, then left to right. We have length plus 1 because we want to avoid dp[r-1]’s r-1 be negative. dp[r] means the matrix[r-1][c]’s maximum side length, so r will start from 1.
We know the top = dp[r-1], left = dp[r], how do we find out topLeft? We first initialize the variable topLeft = 0 at the beginning of the function, topLeft is equal to the last iteration’s old dp[r-1]. In each iteration, we store the old dp[r] to a temp variable, after updating the current dp[r], then we update topLeft = temp, so in the next iteration, we have topLeft be the last iteration’s old dp[r-1].

Solution 2

func maximalSquare(matrix [][]byte) int {
    if matrix == nil || len(matrix) == 0 || len(matrix[0]) == 0 {
        return 0
    }
    row := len(matrix)
    col := len(matrix[0])
    dp := make([]int, row + 1)
    topLeft := 0
    maxSideLength := 0

    for c := 0; c < col; c++ {
        for r := 1; r <= row; r++ {
            temp := dp[r]
            if matrix[r-1][c] == '0' {
                dp[r] = 0
            } else {
                dp[r] = min(dp[r], min(dp[r-1], topLeft)) + 1
            }
            maxSideLength = max(maxSideLength, dp[r])
            topLeft = temp
        }
    }

    return maxSideLength * maxSideLength
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

First Unique Number

You have a queue of integers, you need to retrieve the first unique integer in the queue.

Implement the FirstUnique class:

FirstUnique(int[] nums) Initializes the object with the numbers in the queue.
int showFirstUnique() returns the value of the first unique integer of the queue, and returns -1 if there is no such integer.
void add(int value) insert value to the queue.

Example 1:

Input:
["FirstUnique","showFirstUnique","add","showFirstUnique","add","showFirstUnique","add","showFirstUnique"]
[[[2,3,5]],[],[5],[],[2],[],[3],[]]
Output:
[null,2,null,2,null,3,null,-1]

Explanation:
FirstUnique firstUnique = new FirstUnique([2,3,5]);
firstUnique.showFirstUnique(); // return 2
firstUnique.add(5);            // the queue is now [2,3,5,5]
firstUnique.showFirstUnique(); // return 2
firstUnique.add(2);            // the queue is now [2,3,5,5,2]
firstUnique.showFirstUnique(); // return 3
firstUnique.add(3);            // the queue is now [2,3,5,5,2,3]
firstUnique.showFirstUnique(); // return -1

Example 2:

Input:
["FirstUnique","showFirstUnique","add","add","add","add","add","showFirstUnique"]
[[[7,7,7,7,7,7]],[],[7],[3],[3],[7],[17],[]]
Output:
[null,-1,null,null,null,null,null,17]

Explanation:
FirstUnique firstUnique = new FirstUnique([7,7,7,7,7,7]);
firstUnique.showFirstUnique(); // return -1
firstUnique.add(7);            // the queue is now [7,7,7,7,7,7,7]
firstUnique.add(3);            // the queue is now [7,7,7,7,7,7,7,3]
firstUnique.add(3);            // the queue is now [7,7,7,7,7,7,7,3,3]
firstUnique.add(7);            // the queue is now [7,7,7,7,7,7,7,3,3,7]
firstUnique.add(17);           // the queue is now [7,7,7,7,7,7,7,3,3,7,17]
firstUnique.showFirstUnique(); // return 17

Example 3:

Input:
["FirstUnique","showFirstUnique","add","showFirstUnique"]
[[[809]],[],[809],[]]
Output:
[null,809,null,-1]

Explanation:
FirstUnique firstUnique = new FirstUnique([809]);
firstUnique.showFirstUnique(); // return 809
firstUnique.add(809);          // the queue is now [809,809]
firstUnique.showFirstUnique(); // return -1

Constraints:

1 <= nums.length <= 10^5
1 <= nums[i] <= 10^8
1 <= value <= 10^8
At most 50000 calls will be made to showFirstUnique and add.

Hint 1:

Use doubly Linked list with hashmap of pointers to linked list nodes. add unique number to the linked list. When add is called check if the added number is unique then it have to be added to the linked list and if it is repeated remove it from the linked list if exists. When showFirstUnique is called retrieve the head of the linked list.

Hint 2:

Use queue and check that first element of the queue is always unique.

Hint 3:

Use set or heap to make running time of each function O(logn).

Explanation

New problem!
Similar to [LeetCode] 146. LRU Cache, we need to create a doubly linked list, a hashmap<Integer, Node>, a head and a tail pointer. We use a doubly linked list because we want to keep all unique numbers in this linked list, and have $O(1)$ time complexity for removing the linked list node. We use a hashmap because we want to know if the input number is appeared before or no.
For method showFirstUnique, we can check if the head pointer is null or not. If it’s not null, then we return head.val, else we return -1.
For method add, if the input number is not appeared before, then we put the number and its corresponding node to the map, then add that node to the doubly linked list as tail. Else if the input number appeared before, then we remove its corresponding node from the linked list.

Solution

type Node struct {
    Val int
    Prev *Node
    Next *Node
}

type FirstUnique struct {
    Hm map[int]*Node
    Head *Node
    Tail *Node
}


func Constructor(nums []int) FirstUnique {
    firstUniqueNum := FirstUnique{}
    firstUniqueNum.Hm = make(map[int]*Node)

    for _, num := range nums {
        firstUniqueNum.Add(num)
    }

    return firstUniqueNum
}


func (this *FirstUnique) ShowFirstUnique() int {
    if this.Head == nil {
        return -1
    } else {
        return this.Head.Val
    }
}


func (this *FirstUnique) Add(value int)  {
    if _, ok := this.Hm[value]; ok {
        this.remove(this.Hm[value])
    } else {
        temp := &Node{Val: value}
        this.Hm[value] = temp
        this.setTail(temp)
    }
}

func (this *FirstUnique) setTail(n *Node) {
    if this.Tail != nil {
        this.Tail.Next = n
    }
    n.Prev = this.Tail
    this.Tail = n

    if this.Head == nil {
        this.Head = n
    }
}

func (this *FirstUnique) remove(n *Node) {
    if n.Prev == nil && n != this.Head { return }

    if n.Prev != nil {
        n.Prev.Next = n.Next
    } else {
        this.Head = n.Next
    }

    if n.Next != nil {
        n.Next.Prev = n.Prev
    } else {
        this.Tail = n.Prev
    }

    n.Prev = nil
    n.Next = nil
}


/**
 * Your FirstUnique object will be instantiated and called as such:
 * obj := Constructor(nums);
 * param_1 := obj.ShowFirstUnique();
 * obj.Add(value);
 */

Week 5: April 29th–April 30th

Binary Tree Maximum Path Sum

Given a non-empty binary tree, find the maximum path sum.

For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.

Example 1:

Input: [1,2,3]

       1
      / \
     2   3

Output: 6

Example 2:

Input: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

Output: 42

Explanation

This problem is different from the general path sum problem, in this problem, path sum can starts in non-root, and it can also end in non-leaf.
This kind of path can be concluded in two types:
1. root->leaf path, in example1’s 1->2 or 1->3.
2. Two nodes are connected by their lowest common ancestor (LCA) node, in example1’s 2->1->3.
Apprently, top-down’s recursion method doesn’t work because in type2’s path, its path sum is depends on LCA’s left and right sub path’s maximum, and this type of path sum cannot be obtained from top-down recursion method.
Therefore, we can use bottom-up’s recursion method. Let say node x,
1. Define PS1(x) is from node x to leaf’s first type’s path sum.
2. Define PS2(x) is node x as LCA’s second type path’s path sum.
3. So, if we find all node x’s PS1 and PS2, then we can find the max path sum.
How to find PS1(x) and PS2(x)?
1. PS1(x) and PS2(x) are not less than x-val because x itself can be a single node path.
2. PS1(x) and PS2(x) can be found in PS1(x-left) and PS1(x-right):
  1. PS1(x) = max [ max(PS1(x->left), 0), max(PS1(x->right), 0) ] + x->val
  2. PS2(x) = max(PS1(x->left), 0) + max(PS1(x->right), 0) + x->val
We need to return PS1(x) for its upper layer’s node to calculate PS1 and PS2.

For leaf node, PS1(x) = PS2(x) = x->val.

 class Solution {
 public:
     int maxPathSum(TreeNode *root) {
         int maxSum = INT_MIN;
         int ps1_root = findMaxPathSum(root, maxSum);
         return maxSum;
     }

     int findMaxPathSum(TreeNode *root, int &maxSum) {
         if(!root) return 0;

         int ps1_left = 0, ps1_right = 0;
         if(root->left)
             ps1_left = max(findMaxPathSum(root->left,maxSum),0);
         if(root->right)
             ps1_right = max(findMaxPathSum(root->right,maxSum),0);

         int ps1_root = max(ps1_left, ps1_right) + root->val;
         int ps2_root = ps1_left + ps1_right + root->val;
         maxSum = max(maxSum,max(ps1_root, ps2_root));

         return ps1_root;
     }
 };

From: [LeetCode] 124. Binary Tree Maximum Path Sum

Solution

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxPathSum(root *TreeNode) int {
    res := math.MinInt32
    helper(root, &res)
    return res
}

func helper(root *TreeNode, res *int) int {
    if root == nil { return 0 }

    ps1Left, ps1Right := 0, 0
    if root.Left != nil {
        ps1Left = helper(root.Left, res)
    }
    if root.Right != nil {
        ps1Right = helper(root.Right, res)
    }

    ps1Root := max(0, max(ps1Left, ps1Right)) + root.Val
    ps2Root := ps1Left + ps1Right + root.Val
    *res = max(*res, max(ps1Root, ps2Root))

    return ps1Root
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Check If a String Is a Valid Sequence from Root to Leaves Path in a Binary Tree

Given a binary tree where each path going from the root to any leaf form a valid sequence, check if a given string is a valid sequence in such binary tree.

We get the given string from the concatenation of an array of integers arr and the concatenation of all values of the nodes along a path results in a sequence in the given binary tree.

Example 1:

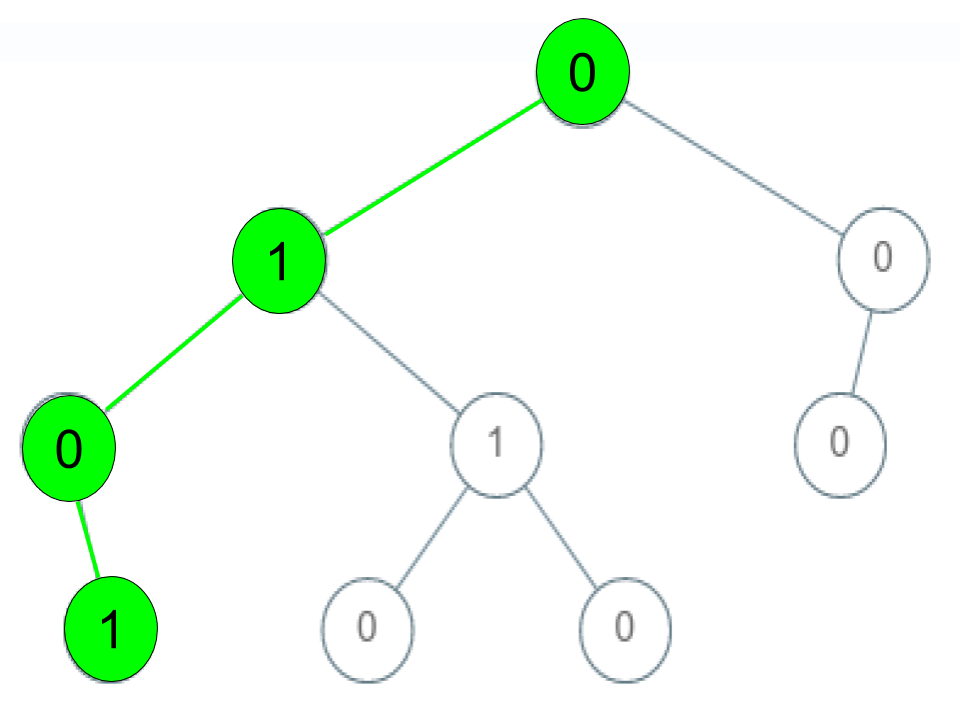
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,0,1]
Output: true
Explanation:
The path 0 -> 1 -> 0 -> 1 is a valid sequence (green color in the figure).
Other valid sequences are:
0 -> 1 -> 1 -> 0
0 -> 0 -> 0

Example 2:

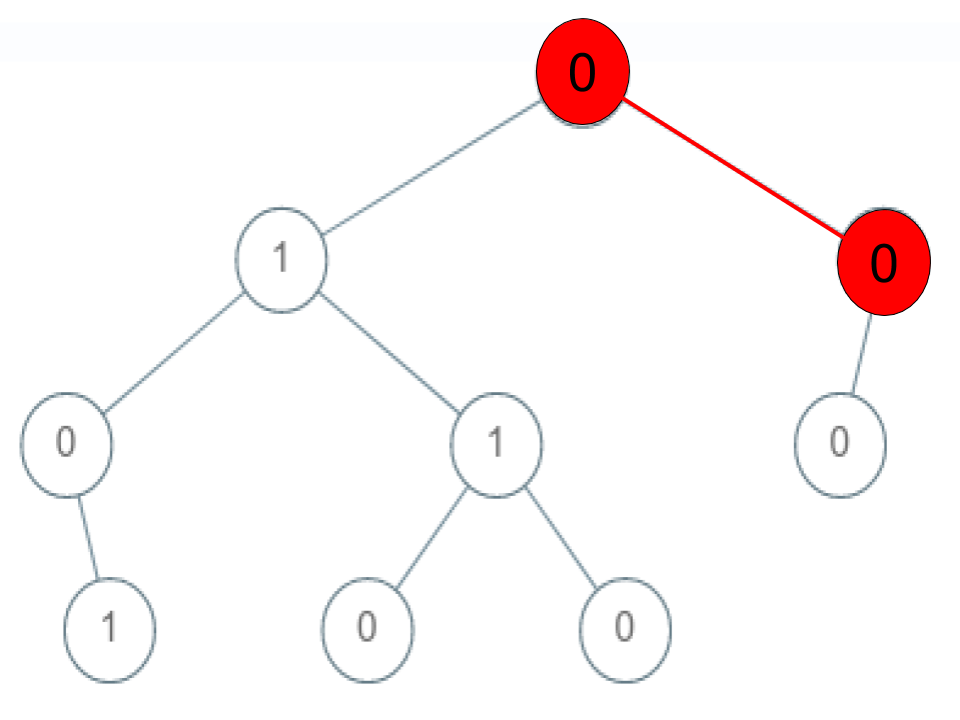
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,0,1]
Output: false
Explanation: The path 0 -> 0 -> 1 does not exist, therefore it is not even a sequence.

Example 3:

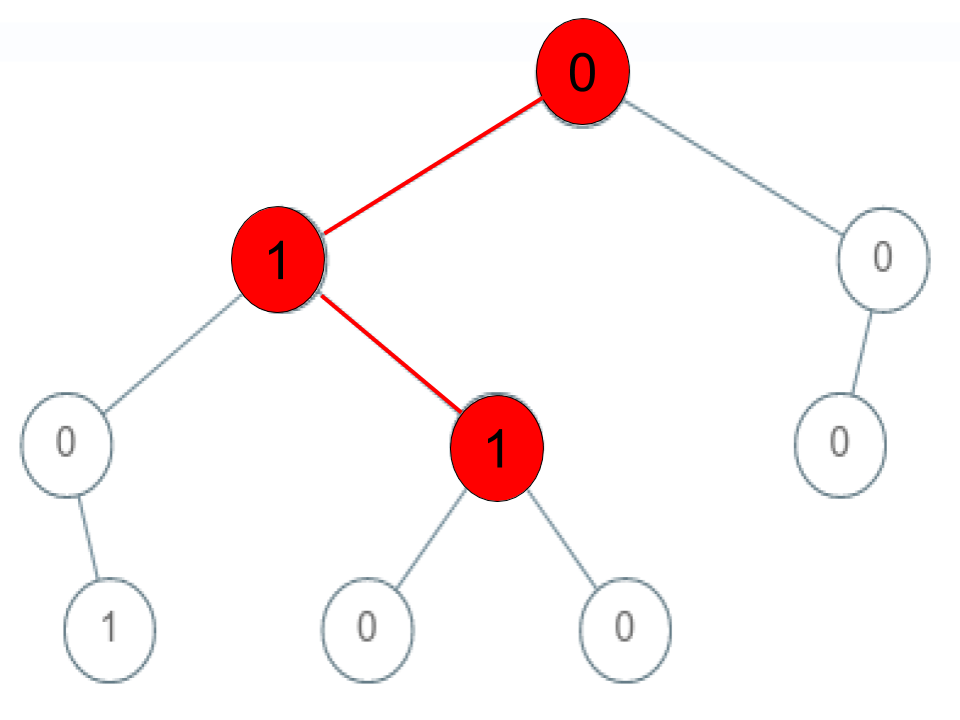
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,1]
Output: false
Explanation: The path 0 -> 1 -> 1 is a sequence, but it is not a valid sequence.

Constraints:

1 <= arr.length <= 5000
0 <= arr[i] <= 9

Each node’s value is between [0 - 9].

Hint 1:

Depth-first search (DFS) with the parameters: current node in the binary tree and current position in the array of integers.

Hint 2:

When reaching at final position check if it is a leaf node.

Explanation 1

New problem and last problem of this 30 day pratice!
We can use DFS to solve this problem. We pass the root node, the array, and the current index to the helper function.
In the helper function, the base case is if the current node is NULL, or the current index is greater than the length of the array, or the current node value is not equal to the current array value, we return false.
If the current node is the leaf node and its value is equal to the current element, and the current element is the last element of the array, we return true.
If the current node is equal to the current element, but it’s not the leaf node, then we recursively call the helper function with the current node’s left child, and call the helper function with its right child, and the current index increase one.

Solution 1

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isValidSequence(root *TreeNode, arr []int) bool {
    return helper(root, arr, 0)
}

func helper(root *TreeNode, arr []int, curIdx int) bool {
    if root == nil || curIdx >= len(arr) || root.Val != arr[curIdx] {
        return false
    }
    if root.Left == nil && root.Right == nil && curIdx == len(arr) - 1 {
        return true
    }
    return helper(root.Left, arr, curIdx + 1) || helper(root.Right, arr, curIdx + 1)
}

Explanation 2

We can also use BFS to solve this problem. We creat a queue and push the current root node to the queue.
Loop the current index from 0 to the last index inclusive and the queue is not empty, then inner loop the queue len(queue) times. Each time, we dequeue to get the current node. If the current node’s value is not equal to the arr[curIdx], then we continue. Else if the current node is the leaf node and current index is the last index, then we return true. Else, we enqueue the current node’s left and right node to the queue. Outside the loop, we return false.

Solution 2

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isValidSequence(root *TreeNode, arr []int) bool {
    queue := make([]*TreeNode, 0)
    queue = append(queue, root)
    for curIdx := 0; curIdx < len(arr) && len(queue) != 0; curIdx++ {
        for i := len(queue); i > 0; i-- {
            curNode := queue[0]
            queue = queue[1:len(queue)]
            if curNode.Val != arr[curIdx] { continue }
            if curNode.Left == nil && curNode.Right == nil && curIdx == len(arr) - 1 { return true }
            if curNode.Left != nil { queue = append(queue, curNode.Left)}
            if curNode.Right != nil { queue = append(queue, curNode.Right)}
        }
    }
    return false
}