Algorithm Problems

Range Update an Array in Constant Time

Given an array arr of size $n$ with all elements initialized to $0$. Implement void add(int[] arr, int l, int r, int num) and void print(int[] arr) which meet the following requirements:

add function: add num to each index between l to index r inclusivle. For example:

arr = [0, 0, 0, 0, 0, 0, 0, 0]

add(arr, 0, 2, 100)
# arr = [100, 100, 100, 0, 0, 0, 0, 0]

add(arr, 1, 5, 100)
# arr = [100, 200, 200, 100, 100, 100, 0, 0]

add(arr, 2, 3, 100)
# arr = [100, 200, 300, 200, 100, 100, 0, 0]

print function: print the final array:

add(arr, 0, 2, 100)
add(arr, 1, 5, 100)
add(arr, 2, 3, 100)
print(arr)
> arr = [100, 200, 300, 200, 100, 100, 0, 0]

For add function, we can simply using a for loop to add the element:

void add(int[] arr, int l, int r, int num) {
    for (int i = l; i <= r; i++) {
        arr[i] += num;
    }
}

But the above function takes $O(n)$ time complexity. In order to make it faster in $O(1)$ time, we do this:

void add(int[] arr, int l, int r, int num) {
    arr[l] += num;
    arr[r+1] -= num;
}

Visualize:

arr = [0, 0, 0, 0, 0, 0, 0]

add(arr, 0, 2, 100)
# arr = [100, 0, 0, -100, 0, 0, 0]

add(arr, 1, 5, 100)
# arr = [100, 100, 0, -100, 0, 0, -100, 0]

add(arr, 2, 3, 100)
# arr = [100, 100, 100, -100, -100, 0, -100, 0]

void print(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        arr[i] += arr[i-1];
    }
}

The first element is not changed, other elements will equal to the sum of its previous element.

Visualize:

# when i = 1:
arr = [100, 200, 100, -100, -100, 0, -100, 0]

# when i = 2:
arr = [100, 200, 300, -100, -100, 0, -100, 0]

# when i = 3:
arr = [100, 200, 300, 200, -100, 0, -100, 0]

# when i = 4:
arr = [100, 200, 300, 200, 100, 0, -100, 0]

# when i = 5:
arr = [100, 200, 300, 200, 100, 100, -100, 0]

# when i = 6:
arr = [100, 200, 300, 200, 100, 100, 0, 0]

# finally when i = 7:
arr = [100, 200, 300, 200, 100, 100, 0, 0]

Find Merge Point of Two Lists

Given two linked lists, find the merge node of these two linked lists.

[LinkedList #1] a--->b--->c
                            \
                            x--->y--->z
                            /
     [LinkedList #2] p--->q

First, we can compare LinkedList 1 and LinkedList 2’s last node, if the last node is different, then these two linkedlists do not have merge node. If the last node is the same, then we compare their sizes, and advance the longer linkedlist by the difference of their sizes. For example, on the above diagram, LinkedList 1 is the longer linkedlist, and we move the current node from a to b. Then, both linked list start at the same time to advance the current node until both linkedlist have the same node, and that node will become the merge node. The code below implements this algorithm:

SinglyLinkedListNode findMergeNode(SinglyLinkedListNode head1, SinglyLinkedListNode head2) {
        SinglyLinkedListNode lastA = findLastNode(head1);
        SinglyLinkedListNode lastB = findLastNode(head2);
        if (lastA != lastB) return -1;

        int lenA = findSize(head1);
        int lenB = findSize(head2);
        int diff = Math.abs(lenA - lenB);
        SinglyLinkedListNode small = lenA <= lenB ? head1 : head2;
        SinglyLinkedListNode large = lenA <= lenB ? head2 : head1;
        while(diff > 0) {
            large = large.next;
            diff--;
        }
        while (small != large) {
            small = small.next;
            large = large.next;
        }
        return large;
    }

Another approach is even simpler. Same as the last approach, first check their last node, if they do not have the same last node, then there is no merge node. Else, iterate both linkedlist at the same time, if one linkedlist reach the end, start from another linkedlist, until they have the same node. Then that node is the merge node.

Node FindMergeNode(Node headA, Node headB) {
    // check the last nodes if they are the same

    Node currentA = headA;
    Node currentB = headB;

    while (currentA != currentB) {
        if (currentA.next == null) {
            currentA = headB;
        } else {
            currentA = currentA.next;
        }
        if (currentB.next == null) {
            currentB = headA;
        } else {
            currentB = currentB.next;
        }
    }
    return currentB;
}

Explanation:

If the first linkedlist has size $x$, merge point is at the $i$ node. The second linkedlist has size $y$, merge point is at the $j$ node.

The first linkedlist needs to travel $i$ steps to reach the merge node, and $x-i$ steps to reach the end of the first linkedlist. Then, it takes $j$ steps on the second linkedlist to reach the merge node again. Similarly, the second linkedlist needs to travel $j$ steps to reach the merge node, and $y-j$ steps to reach the end. Then, it takes $i$ steps on the first linkedlist to reach the merge node.

FirstLinkedList reaches the merge node the second times: $i + (x-i) + j$. SecondLinkedList reaches the merge node the second times: $j + (y-j) + i$.

Since the size from the beginning of merge node to the end is the same for both linkedlist, which means $x-i = y-j$. Therefore, both linkedlists will travel to the merge node at the same number of steps.

Implement Regular Expression Matching

Given a string and a pattern with support for . and *, return true if the string matches the pattern, otherwise return false. For example:

boolean isMatch(String s, String p)

isMatch("ab", "ab")    // return true
isMatch("ab", "cb")    // return false
isMatch("ab", ".b")    // return true
isMatch("aab", "a*b")  // return true
isMatch("ab", "x*ab")  // return true
isMatch("ab", ".*b")   // retrun true

It is easy to think about if the pattern only has one character, if that character is not a . and it is not equals to the first character of the string, then we return false.

If the pattern has length at least two, then we consider the second character of pattern, if it is a * or it is not a *.

If the second character is not a *, then we simply check if the first characters are matching, if the first character is not matches, we simply return false, it the first characters are match, then recursivly call the isMatch for both strings starting from their second characters.

If the second character is a *, then we need to consider case 1: * is functions for zero of the first character, and case 2 is * is functions for one or more of the first character.

Case 1: we can simply call isMatch for the original string and the pattern starts from the third character.

Case 2: while the first character of string matches the first character of pattern, we iterates the next character of string and compare it with the first character of pattern until they do not match, we call isMatch for the character of string that does not match the first character with the pattern starts from the third character.

int i = 0;
while(s.charAt(i) == p.charAt(0)) {
    i++;
}
isMatch(s.chatAt(i), p.charAt(2))

But this approach does not work, because if the first character of the pattern is ., then it always matches the first character of the string and the iterative one. Consider this isMatch("aaab", ".*b"). So, after we check the i character matches the first character of the pattern, we need to check isMatch(s.substring(i + 1), p.substring(2)), if it mathes, we can simply return true as the result. If they do not match, it’s fine, we still increase i. If i is greater than s.length(), then we return false.

while (i < s.length() && (s.charAt(i) == p.charAt(0) || p.charAt(0)=='.') ) {
    if (isMatch(s.substring(i + 1), p.substring(2))) {
        return true;
    }
    i++;
}
return false;

The final code is below:

public boolean isMatch(String s, String p) {
    // base case
    if (p.length() == 0) {
        return s.length() == 0;
    }

    // special case
    if (p.length() == 1) {

        // if the length of s is 0, return false
        if (s.length() < 1) {
            return false;
        }

        //if the first does not match, return false
        else if ((p.charAt(0) != s.charAt(0)) && (p.charAt(0) != '.')) {
            return false;
        }

        // otherwise, compare the rest of the string of s and p.
        else {
            return isMatch(s.substring(1), p.substring(1));
        }
    }

    // case 1: when the second char of p is not '*'
    if (p.charAt(1) != '*') {
        if (s.length() < 1) {
            return false;
        }
        if ((p.charAt(0) != s.charAt(0)) && (p.charAt(0) != '.')) {
            return false;
        } else {
            return isMatch(s.substring(1), p.substring(1));
        }
    }

    // case 2: when the second char of p is '*', complex case.
    else {
        //case 2.1: a char & '*' can stand for 0 element
        if (isMatch(s, p.substring(2))) {
            return true;
        }

        //case 2.2: a char & '*' can stand for 1 or more preceding element,
        //so try every sub string
        int i = 0;
        while(i<s.length() && (s.charAt(i)==p.charAt(0) || p.charAt(0)=='.') ){
            if (isMatch(s.substring(i + 1), p.substring(2))) {
                return true;
            }
            i++;
        }
        return false;
    }
}

// Source: https://www.programcreek.com/2012/12/leetcode-regular-expression-matching-in-java/

Maintain Decreasing Order of Numbers in an Array

Given an array of numbers, each time if the number with index $i$ is greater than the number of index $i-1$, then the number with index $i$ will be removed. The question is after how many times, no element will be removed. For example,

Given an array p = [6, 5, 8, 7, 4, 7, 3, 1, 1, 10].

On day 1, p = [6, 5, 7, 4, 3, 1, 1]

On day 2, p = [6, 5, 4, 3, 1, 1]

So after 2 days, no element will be removed.

First, we can simply come up with the idea that loop through the array and save all indexes that have the value greater than its previous element to a list. Then, we remove these elements according to the saved index list. Repeat this process until all elements maintain the decreasing order.

In this approach, we take $O(N)$ to loop through the array, and take $O(N)$ to remove each element. Therefore, it takes $O(n^2)$ time complexity.

The remove instruction takes a lot of time, how can we make it faster?

The answer is it can be done with linkedlist of linkedlst, for example,

Day 0, [6 5 8 7 4 7 3 1 1 10], we can write it as 6->5, 8->7->4, 7->3->-1->1, 10, each sublist is the longest decreasing order sublist it can be.

Day 1, we remove the first element of the sublist except the first sublist:

6->5, 7->4, 3->1->1

Now, we check to see if sublist can merge, here the second sublist’s last element is greater than the first element of the thrid sublist, so they can be merged:

6->5, 7->4->3->1->1

Day 2, we remove the first element of the sublist except the first sublist:

6->5, 4->3->1->1

Now, we see that they can be merged to a single sublist and we are done:

6->5->4->3->1->1

In this approach, the remove instruction takes $O(1)$ time complexity, and therefore it’s faster.

Final code is below:

class Node {
    int value;
    Node next;

    Node(int value) {
        this.value = value;
    }
}

class MyList {
    Node head;
    Node tail;

    void append(int value) {
        Node node = new Node(value);
        if (tail == null) {
            head = node;
        } else {
            tail.next = node;
        }
        tail = node;
    }

    void append(MyList list) {
        tail.next = list.head;
        tail = list.tail;
    }

    void removeFirst() {
        head = head.next;
        if (head == null) {
            tail = null;
        }
    }

    void printStr() {
        Node current = head;
        while (current != null) {
            System.out.print(current.value + " ");
            current = current.next;
        }
        System.out.println();
    }
}

static int poisonousPlants(int[] p) {
    List<MyList> out = new ArrayList<MyList>();
    MyList lastLst = null;
    for (int i = 0; i < p.length; i++) {
        if (i > 0 && p[i] <= p[i - 1]) {
            lastLst.append(p[i]);
        } else {
            MyList base = new MyList();
            base.append(p[i]);

            out.add(base);
            lastLst = base;
        }
    }

    int day = 0;
    while (out.size() > 1) {
        for (int i = 1; i < out.size(); i++) {
            // remove the first element of the sublist except the first sublist
            out.get(i).removeFirst();
        }

        List<MyList> updateOut = new ArrayList<MyList>();
        for (MyList lst : out) {
            if (lst.head == null) {
                // after remove the first element of sublist, if it is null, we just ignore it.
                continue;
            }

            if (!updateOut.isEmpty() && updateOut.get(updateOut.size() - 1).tail.value >= lst.head.value) {
                // if the last element of sublist i is greater than the first element of sublist i+1,
                // we merge them
                updateOut.get(updateOut.size() - 1).append(lst);
            } else {
                // adding back the sublist into the outer list
                updateOut.add(lst);
            }
        }

        // update the outer list
        out = updateOut;

        day++;
    }
    return day;
}

// Source: https://github.com/charles-wangkai/hackerrank/blob/master/poisonous-plants/Solution.java

QuickSort QuickSelect TopK

QuickSort algorithm

import java.util.*;

class Main {
    static void swap (int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

    static int partition(int[] arr, int start, int end) {
        int pivot = arr[start];
        int left = start+1;
        int right = end;
        while (left <= right) {
            if (arr[left] > pivot && arr[right] < pivot) {
                swap(arr, left, right);
            }
            if (arr[left] <= pivot) left += 1;
            if (arr[right] >= pivot) right -= 1;
        }
        swap(arr, start, right);
        return right;
    }

    static void quickSort(int[] arr, int start, int end) {
        int partition = partition(arr, start, end);
        if (partition-1 > start) {
            quickSort(arr, start, partition-1);
        }
        if (partition+1 < end) {
            quickSort(arr, partition+1, end);
        }
    }

    public static void main (String[] args) {
        int[] arr = {2, 2, 3, 1, 2};
        quickSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
}

Kth Largest Element in an Array

Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.

class Solution {
    void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }

    int partition(int[] nums, int start, int end) {
        int pivot = nums[start];
        int left = start + 1;
        int right = end;
        while (left <= right) {
            if (nums[left] < pivot && nums[right] > pivot) {
                swap(nums, left, right);
            }
            if (nums[left] >= pivot) left += 1;
            if (nums[right] <= pivot) right -= 1;
        }
        swap(nums, start, right);
        return right;
    }

    public int findKthLargest(int[] nums, int k) {
        int start = 0, end = nums.length - 1;
        while (start <= end) {
            int p = partition(nums, start, end);
            if (k-1 == p) return nums[k-1];
            else if (p > k-1) end = p-1;
            else if (p < k-1) start = p+1;
        }

        return -1;
    }
}

MergeSort

MergeSort Algorithm

import java.util.*;

class Main {
    static void merge(int[] arr, int start, int mid, int end) {
        int[] sortedArr = new int[end - start + 1];
        int i = start;
        int j = mid + 1;
        int k = 0;

        while (i <= mid && j <= end) {
            if (arr[i] <= arr[j]) {
                sortedArr[k++] = arr[i++];
            } else {
                sortedArr[k++] = arr[j++];
            }
        }
        while (i <= mid) {
            sortedArr[k++] = arr[i++];
        }
        while (j <= end) {
            sortedArr[k++] = arr[j++];
        }

        System.arraycopy(sortedArr, 0, arr, start, end-start+1);
    }

    static void mergeSort(int[] arr, int start, int end) {
        if (start >= end) return;
        int mid = start + (end - start) / 2;
        mergeSort(arr, start, mid);
        mergeSort(arr, mid+1, end);
        merge(arr, start, mid, end);
    }

    public static void main (String[] args) {
        int[] arr = new int[] {1, 1, 3, 9, 2, 5, 8, 7, 7};
        mergeSort(arr, 0, arr.length-1);
        System.out.println(Arrays.toString(arr));
    }
}

Reverse Pairs

Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2*nums[j].

You need to return the number of important reverse pairs in the given array.

Example1:

Input: [1,3,2,3,1]
Output: 2

Example2:

Input: [2,4,3,5,1]
Output: 3

class Solution {
    int mergeSort(int[] nums, int lo, int hi) {
        if (lo >= hi) return 0;
        int res = 0;
        int mid = lo + (hi - lo) / 2;

        res += mergeSort(nums, lo, mid);
        res += mergeSort(nums, mid+1, hi);
        res += merge(nums, lo, mid, hi);

        return res;
    }

    int merge(int[] nums, int lo, int mid, int hi) {
        int count = 0;
        int[] arr = new int[hi - lo + 1];
        int p = lo, q = mid + 1;
        while (p <= mid && q <= hi) {
            if ((long)nums[p] > (long)nums[q] * 2) {
                count += mid - p + 1;
                q += 1;
            } else {
                p += 1;
            }
        }

        p = lo;
        q = mid + 1;
        int index = 0;
        while (p <= mid && q <= hi) {
            if (nums[p] <= nums[q]) {
                arr[index++] = nums[p++];
            } else {
                arr[index++] = nums[q++];
            }
        }

        while (p <= mid) {
            arr[index++] = nums[p++];
        }
        while (q <= hi) {
            arr[index++] = nums[q++];
        }

        System.arraycopy(arr, 0, nums, lo, hi-lo+1);

        return count;
    }

    public int reversePairs(int[] nums) {
        return mergeSort(nums, 0, nums.length-1);
    }
}

Topological Sort

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u->v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.

For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 0 3 1”. The first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no incoming edges). One example for Topological Sort is build dependency problem. If dependencyA depends on dependencyB and dependencyC, then dependencyA can be resolved anytime after dependencyB and dependencyC are resolved.

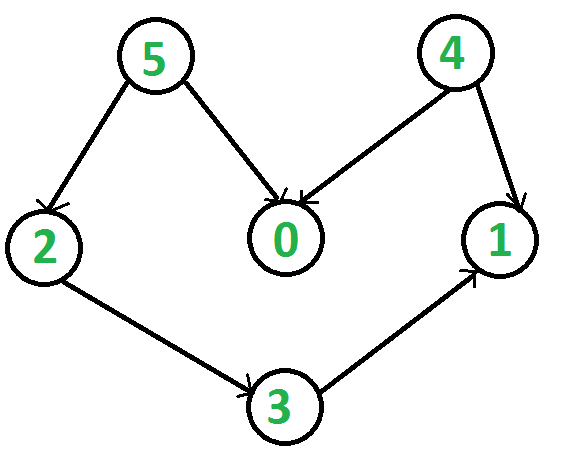
Topological Sorting vs Depth First Traversal (DFS):

For example, in the given graph, the vertex ‘5’ should be printed before vertex ‘0’, but unlike DFS, in topological sort, the vertex ‘4’ should also be printed before vertex ‘0’. So Topological sorting is different from DFS. For example, a DFS of the shown graph is “5 2 3 1 0 4”, but it is not a topological sorting.

TopologicalSort using Queue

import java.util.*;

class Graph {
    private int numVertices; // Number of vertices
    private List<Integer>[] adjLst; // Adjacency List

    // Constructor
    Graph(int n) {
        numVertices = n;
        adjLst = new LinkedList[numVertices];
        for (int i = 0; i < numVertices; ++i) {
            adjLst[i] = new LinkedList<>();
        }
    }

    public void addEdge(int u, int v) {
        adjLst[u].add(v);
    }

    public int getNumVertices() {
        return numVertices;
    }

    public List<Integer>[] getAdj() {
        return this.adjLst;
    }
}

public class Main {
    public static List<Integer> topologicalSort(Graph g) {
        List<Integer> res = new ArrayList<>();

        int numVertices = g.getNumVertices();
        int[] inDegree = new int[numVertices];

        List<Integer>[] adjacencyList = g.getAdj();
        for (List<Integer> lst : adjacencyList) {
            for (int v : lst) {
                inDegree[v]++;
            }
        }

        Queue<Integer> queue = new LinkedList<>();

        // start from nodes with in degree 0
        for (int i = 0; i < numVertices; i++) {
            if (inDegree[i] == 0)
                queue.offer(i);
        }

        while (!queue.isEmpty()) {
            int curr = queue.poll();
            res.add(curr);
            for (int child : adjacencyList[curr]) {
                inDegree[child]--;
                if (inDegree[child] == 0) {
                    queue.offer(child);
                }
            }
        }

        return res.size() == numVertices ? res : new ArrayList<>();
    }

    public static void main(String args[]) {
        Graph g = new Graph(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);

        List<Integer> res = topologicalSort(g);
        System.out.println(res.toString());
    }
}

TopologicalSort using Stack

import java.util.*;

class Graph {
    private int numVertices; // Number of vertices
    private List<Integer>[] adjLst; // Adjacency List

    // Constructor
    Graph(int n) {
        numVertices = n;
        adjLst = new LinkedList[numVertices];
        for (int i = 0; i < numVertices; ++i) {
            adjLst[i] = new LinkedList<>();
        }
    }

    public void addEdge(int u, int v) {
        adjLst[u].add(v);
    }

    public int getNumVertices() {
        return numVertices;
    }

    public List<Integer>[] getAdj() {
        return this.adjLst;
    }
}

public class Main {
    private static void helper(int u, Stack<Integer> stack, Set<Integer> visited, List<Integer>[] adjLst) {
        visited.add(u);
        for (int v : adjLst[u]) {
            if (visited.contains(v)) {
                continue;
            }
            helper(v, stack, visited, adjLst);
        }
        stack.push(u);
    }

    public static List<Integer> topologicalSort(Graph graph) {
        Stack<Integer> stack = new Stack<>();
        Set<Integer> visited = new HashSet<>();
        List<Integer>[] adjLst = graph.getAdj();
        int numVertices = graph.getNumVertices();

        for (int u = 0; u < numVertices; u++) {
            if (visited.contains(u)) {
                continue;
            }
            helper(u, stack, visited, adjLst);
        }

        List<Integer> res = new ArrayList<>();
        while (!stack.isEmpty()) {
            res.add(stack.pop());
        }

        return res.size() == numVertices ? res : new ArrayList<>();
    }

    public static void main(String args[]) {
        Graph g = new Graph(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);

        List<Integer> res = topologicalSort(g);
        System.out.println(res.toString());
    }
}

Source:

Topological Sorting