Binary Tree Traversal

Posted on | In

Binary Tree Traversal

In tree traversal, we have pre-order traversal, in-order traversal, post-order traversal and level-order traversal. This post concludes all these traversals’ implementation.

Pre-order Traversal

Given a tree below, the pre-order traversal will be [1, 2, 3].

1
2
3
4
5
6
7
8
Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,2,3]

Recursive

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    void helper(TreeNode root, List<Integer> res) {
        if (root == null) return;
        res.add(root.val);
        helper(root.left, res);
        helper(root.right, res);
    }

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }
}

Iterative

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;

        TreeNode p = root;
        Stack<TreeNode> st = new Stack<>();

        while (p != null || !st.isEmpty()) {
            if (p != null) {
                res.add(p.val);
                st.push(p);
                p = p.left;
            } else {
                TreeNode temp = st.pop();
                p = temp.right;
            }
        }

        return res;
    }
}

In-order Traversal

Recursive

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    void helper(TreeNode root, List<Integer> res) {
        if (root == null) return;
        helper(root.left, res);
        res.add(root.val);
        helper(root.right, res);
    }

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }
}

Iterative

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;

        TreeNode p = root;
        Stack<TreeNode> st = new Stack<>();

        while (p != null || !st.isEmpty()) {
            if (p != null) {
                st.push(p);
                p = p.left;
            } else {
                p = st.pop();
                res.add(p.val);
                p = p.right;
            }
        }

        return res;
    }
}

Post-order Traversal

1
2
3
4
5
6
7
8
Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [3,2,1]

Recursive

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    void helper(TreeNode root, List<Integer> res) {
        if (root == null) return;
        helper(root.left, res);
        helper(root.right, res);
        res.add(root.val);
    }

    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        helper(root, res);
        return res;
    }
}

Iterative

Similar to pre-order traversal’s root -> left -> right, this time we traverse root -> right -> left. At the end, we reverse the result list to get left -> right -> root.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;

        TreeNode p = root;
        Stack<TreeNode> st = new Stack<>();

        while (p != null || !st.isEmpty()) {
            if (p != null) {
                res.add(p.val);
                st.push(p);
                p = p.right;
            } else {
                TreeNode temp = st.pop();
                p = temp.left;
            }
        }

        Collections.reverse(res);
        return res;
    }
}

Lever-order Traversal

1
2
3
4
5
6
7
8
9
10
11
12
13
Input: [3,9,20,null,null,15,7]
    3
   / \
  9  20
    /  \
   15   7

Output:
[
  [3],
  [9,20],
  [15,7]
]

Iterative

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;

        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);

        while(!q.isEmpty()) {
            List<Integer> cur = new ArrayList<>();
            for (int i = q.size() - 1; i >= 0; i--) {
                TreeNode popNode = q.poll();
                cur.add(popNode.val);
                if (popNode.left != null) q.offer(popNode.left);
                if (popNode.right != null) q.offer(popNode.right);
            }
            res.add(cur);
        }

        return res;
    }
}

Recursive

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    void helper(TreeNode root, List<List<Integer>> res, int level) {
        if (root == null) return;
        if (level == res.size()) {
            res.add(new ArrayList<>());
        }
        res.get(level).add(root.val);
        helper(root.left, res, level+1);
        helper(root.right, res, level+1);
    }

    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        helper(root, res, 0);
        return res;
    }
}

Morris Traversal

We can use morris traversal to traverse in-order, pre-order, post-order in $O(n)$ time, $O(1)$ space.

In-order Traversal

  1. If the current node’s left child is null, print out current node, and its right child becomes current node.
  2. If the current node’s left child is not null, in current node’s left subtree, find the current node’s in-order traversal predecessor, in other word, find the node before the current node in the order of in-order traversal.
    1. If the predecessor node’s right child is null, set its right child to current node. Current node’s left child becomes current node.
    2. If the predecessor node’s right child is current node, set its right child to null. Print out current node. Current node’s right child becomes current node.
  3. Repeat step 1 and step 2 until current node is null.

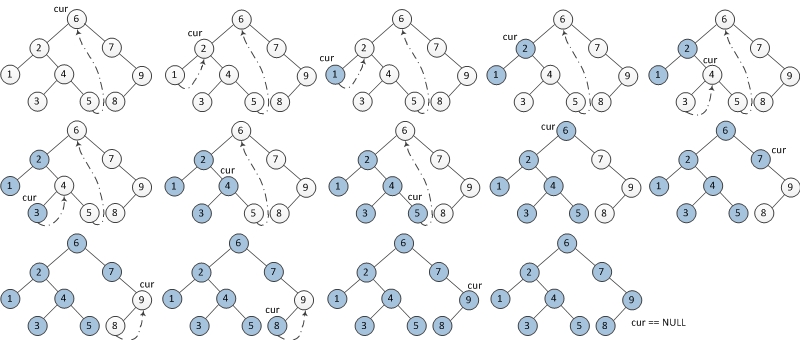
In-order Traversal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        TreeNode cur = root;
        TreeNode pre = null;

        while (cur != null) {
            if (cur.left == null) {    // 1
                res.add(cur.val);
                cur = cur.right;
            } else {
                pre = cur.left;
                while (pre.right != null && pre.right != cur) {
                    pre = pre.right;
                }
                if (pre.right == null) {    // 2.a
                    pre.right = cur;
                    cur = cur.left;
                } else if (pre.right == cur) {    // 2.b
                    pre.right = null;
                    res.add(cur.val);
                    cur = cur.right;
                }
            }
        }

        return res;
    }
}

Pre-order Traversal

  1. If the current node’s left child is null, print out current node, and its right child becomes current node.
  2. If the current node’s left child is not null, in current node’s left subtree, find the current node’s in-order traversal predecessor.
    1. If the predecessor node’s right child is null, set its right child to current node. Print out current node. Current node’s left child becomes current node.
    2. If the predecessor node’s right child is current node, set its right child to null. Current node’s right child becomes current node.
  3. Repeat step 1 and step 2 until current node is null.

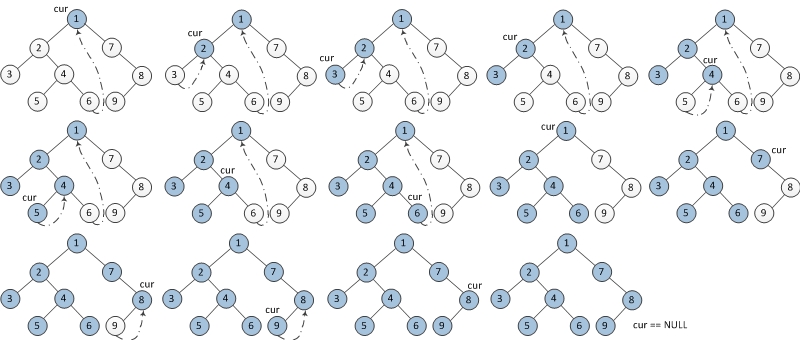
Pre-order Traversal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        TreeNode cur = root;
        TreeNode pre = null;

        while (cur != null) {
            if (cur.left == null) {
                res.add(cur.val);
                cur = cur.right;
            } else {
                pre = cur.left;
                while (pre.right != null && pre.right != cur) {
                    pre = pre.right;
                }
                if (pre.right == null) {
                    pre.right = cur;
                    res.add(cur.val);    // different from in-order traversal
                    cur = cur.left;
                } else if (pre.right == cur) {
                    pre.right = null;
                    cur = cur.right;
                }
            }
        }

        return res;
    }
}

Post-order Traversal

Before we start, we create a dump TreeNode, and make its left child be the root node. Current node set to the dump node.

  1. If the current node’s left child is null, set its right child becomes current node.
  2. If the current node’s left child is not null, in current node’s left subtree, find the current node’s in-order traversal predecessor.
    1. If the predecessor node’s right child is null, set its right child to current node. Current node’s left child becomes current node.
    2. If the predecessor node’s right child is current node, set its right child to null. Reversly print out all the nodes from the current node’s left child to the predecessor node. Current node’s right child becomes current node.
  3. Repeat step 1 and step 2 until current node is null.

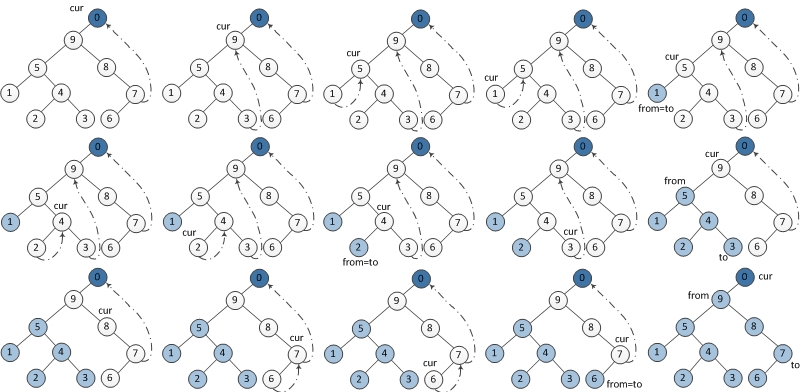
Post-order Traversal

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution {
    void reverse(TreeNode from, TreeNode to) {
        if (from == to) return;
        TreeNode x = from;
        TreeNode y = from.right;
        TreeNode z = null;

        while (true) {
            z = y.right;
            y.right = x;
            x = y;
            y = z;
            if (x == to) {
                break;
            }
        }
    }

    void addReverse(TreeNode from, TreeNode to, List<Integer> res) {
        reverse(from, to);
        TreeNode p = to;
        while (true) {
            res.add(p.val);
            if (p == from) {
                break;
            }
            p = p.right;
        }
        reverse(to, from);
    }

    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        TreeNode dump = new TreeNode(-1);
        dump.left = root;
        TreeNode cur = dump;
        TreeNode pre = null;

        while (cur != null) {
            if (cur.left == null) {
                cur = cur.right;
            } else {
                pre = cur.left;
                while (pre.right != null && pre.right != cur) {
                    pre = pre.right;
                }
                if (pre.right == null) {
                    pre.right = cur;
                    cur = cur.left;
                } else if (pre.right == cur) {
                    pre.right = null;
                    addReverse(cur.left, pre, res);
                    cur = cur.right;
                }
            }
        }

        return res;
    }
}

Source:

Morris Traversal方法遍历二叉树（非递归，不用栈，O(1)空间）