Processing math: 100%

December LeetCoding Challenge

Posted on | In

Last month of 2020! Except went to wework office in Feburary, all other days I have been working from home. Let’s continue December LeetCoding Challenge.

Week 1: December 1st - December 7th

Shortest Word Distance

Given a list of words and two words word1 and word2, return the shortest distance between these two words in the list.

Example:

Assume that words = ["practice", "makes", "perfect", "coding", "makes"].

1
2
Input: word1 = “coding”, word2 = “practice”
Output: 3

1
2
Input: word1 = "makes", word2 = "coding"
Output: 1

Note:

You may assume that word1 does not equal to word2, and word1 and word2 are both in the list.

Explanation

  1. We can use idx1 points to the most recent word1’s index and idx2 points to the most recent word2’s index. Loop all the words, when we find both words, we can calculate their distance by abs(idx1 - idx2).

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int shortestDistance(String[] words, String word1, String word2) {
        int res = words.length;
        int idx1 = -1, idx2 = -1;

        for (int i = 0; i < words.length; i++) {
            if (words[i].equals(word1)) idx1 = i;
            if (words[i].equals(word2)) idx2 = i;
            if (idx1 != -1 && idx2 != -1) {
                res = Math.min(res, Math.abs(idx1-idx2));
            }
        }

        return res;
    }
}

Maximum Depth of Binary Tree

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

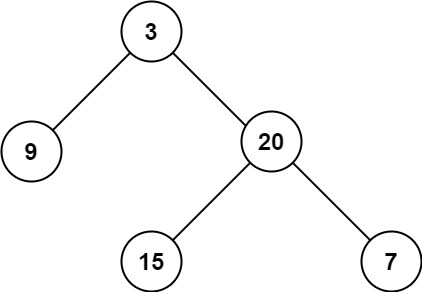
Maximum Depth of Binary Tree

1
2
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

1
2
Input: root = [1,null,2]
Output: 2

Example 3:

1
2
Input: root = []
Output: 0

Example 4:

1
2
Input: root = [0]
Output: 1

Constraints:

  • The number of nodes in the tree is in the range [0, 10^4].

  • -100 <= Node.val <= 100

Explanation

  1. We want to find the maximum height of the tree, which means we need to find the height of the left subtree plus one and the height of the right subtree plus one. Compare both and take the maximum.

  2. The base case is if the root tree node is NULL, we return 0.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxDepth(root *TreeNode) int {
    if root == nil { return 0 }
    return 1 + max(maxDepth(root.Left), maxDepth(root.Right))
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Linked List Random Node

Given a singly linked list, return a random node’s value from the linked list. Each node must have the same probability of being chosen.

Follow up:

What if the linked list is extremely large and its length is unknown to you? Could you solve this efficiently without using extra space?

Example:

1
2
3
4
5
6
7
8
// Init a singly linked list [1,2,3].
ListNode head = new ListNode(1);
head.next = new ListNode(2);
head.next.next = new ListNode(3);
Solution solution = new Solution(head);

// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
solution.getRandom();

Explanation

  1. We don’t need to know the size of the linked list, we can use Reservoir Sampling to solve this problem.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
type Solution struct {
    Head *ListNode
}


/** @param head The linked list's head.
        Note that the head is guaranteed to be not null, so it contains at least one node. */
func Constructor(head *ListNode) Solution {
    return Solution{Head: head}
}


/** Returns a random node's value. */
func (this *Solution) GetRandom() int {
    res := this.Head.Val
    cur := this.Head.Next
    j := 2
    for cur != nil {
        r := rand.Intn(j)
        if r == 0 { res = cur.Val }
        j += 1
        cur = cur.Next
    }
    return res
}


/**
 * Your Solution object will be instantiated and called as such:
 * obj := Constructor(head);
 * param_1 := obj.GetRandom();
 */

Increasing Order Search Tree

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

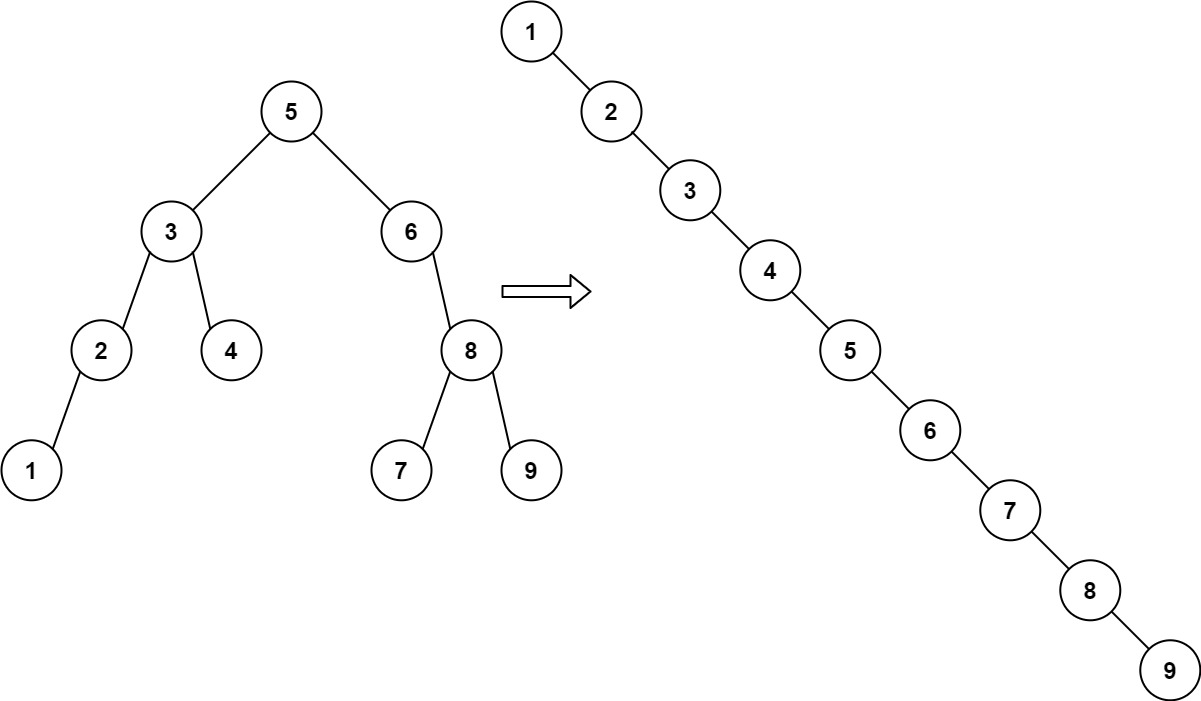
Increasing Order Search Tree

1
2
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

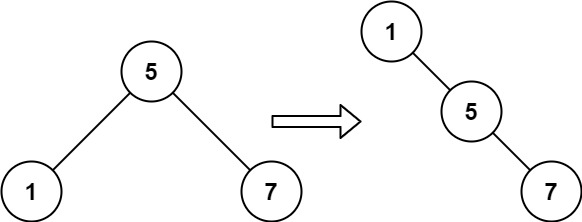
Increasing Order Search Tree

1
2
Input: root = [5,1,7]
Output: [1,null,5,null,7]

Constraints:

  • The number of nodes in the given tree will be in the range [1, 100].

  • 0 <= Node.val <= 1000

Explanation 1

  1. We can traverse the tree using in-order traversal and store every node into a list.

  2. After traversing all the nodes and store into a list, we can generate the result tree by traversing the list.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func increasingBST(root *TreeNode) *TreeNode {
    lst := make([]*TreeNode, 0)
    helper(root, &lst)

    res := &TreeNode{}
    cur := res
    for _, node := range lst {
        cur.Right = &TreeNode{Val: node.Val}
        cur = cur.Right
    }
    return res.Right
}

func helper(root *TreeNode, lst *[]*TreeNode) {
    if root == nil { return }
    helper(root.Left, lst)
    *lst = append(*lst, root)
    helper(root.Right, lst)
}

Explanation 2

  1. We can generate the result tree on the fly when we are traversing, we just need a global pointer cur pointing to the right leaf of the result tree, then every node is added to cur.right then we update cur = cur.right.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func increasingBST(root *TreeNode) *TreeNode {
    dummy := &TreeNode{}
    cur := dummy
    helper(root, &cur)
    return dummy.Right
}

func helper(root *TreeNode, cur **TreeNode) {
    if root == nil { return }
    helper(root.Left, cur)
    (*cur).Right = &TreeNode{Val: root.Val}
    *cur = (*cur).Right
    helper(root.Right, cur)
}

The kth Factor of n

Given two positive integers n and k.

A factor of an integer n is defined as an integer i where n % i == 0.

Consider a list of all factors of n sorted in ascending order, return the kth factor in this list or return -1 if n has less than k factors.

Example 1:

1
2
3
Input: n = 12, k = 3
Output: 3
Explanation: Factors list is [1, 2, 3, 4, 6, 12], the 3rd factor is 3.

Example 2:

1
2
3
Input: n = 7, k = 2
Output: 7
Explanation: Factors list is [1, 7], the 2nd factor is 7.

Example 3:

1
2
3
Input: n = 4, k = 4
Output: -1
Explanation: Factors list is [1, 2, 4], there is only 3 factors. We should return -1.

Example 4:

1
2
3
Input: n = 1, k = 1
Output: 1
Explanation: Factors list is [1], the 1st factor is 1.

Example 5:

1
2
3
Input: n = 1000, k = 3
Output: 4
Explanation: Factors list is [1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500, 1000].

Constraints:

  • 1 <= k <= n <= 1000

Hint 1:

The factors of n will be always in the range [1, n].

Hint 2:

Keep a list of all factors sorted. Loop i from 1 to n and add i if n % i == 0. Return the kth factor if it exist in this list.

Explanation 1

  1. We can solve this in O(n) time complexity. Loop i from 1 to n inclusive, if we find a factor then we decrease k. When k is 0, we return the factor i. After the loop, that means we can’t find the kth factor so we return -1.

Solution 1

1
2
3
4
5
6
7
8
9
10
func kthFactor(n int, k int) int {
    for i := 1; i <= n; i++ {
        if n % i == 0 {
            k -= 1
            if k == 0 { return i }
        }
    }

    return -1
}

Explanation 2

  1. We can solve this in O(sqrt(n)) time complexity. If n = 16, when we find a factor 1, then we know 16 is 1’s corresponding factor; when we find a factor 2, then 8 is its corresponding factor; when we find a factor 4, then 4 is itself’s corresponding factor. So we can loop from 1 to sqrt(n) inclusive then we find all the factors as [1, 2, 4, 8, 16].

  2. First, we loop i from 1 to 2 inclusive. When n % i == 0 && --k == 0, then we know i is the kth factor.

  3. After the above loop, that means k is in the second half. We can loop i from 4 to 1 backward inclusive. When n % i == 0 && --k == 0, then the kth factor is the factor i’s corresponding factor n / i.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func kthFactor(n int, k int) int {
    for i := 1; i * i < n; i++ {
        if n % i == 0 {
            k -= 1
            if k == 0 { return i }
        }
    }

    for i := int(math.Sqrt(float64(n))); i >= 1; i-- {
        if n % i == 0 {
            k -= 1
            if k == 0 { return n / i }
        }
    }

    return -1
}

Can Place Flowers

You have a long flowerbed in which some of the plots are planted, and some are not. However, flowers cannot be planted in adjacent plots.

Given an integer array flowerbed containing 0’s and 1’s, where 0 means empty and 1 means not empty, and an integer n, return if n new flowers can be planted in the flowerbed without violating the no-adjacent-flowers rule.

Example 1:

1
2
Input: flowerbed = [1,0,0,0,1], n = 1
Output: true

Example 2:

1
2
Input: flowerbed = [1,0,0,0,1], n = 2
Output: false

Constraints:

  • 1 <= flowerbed.length <= 2 * 10^4

  • flowerbed[i] is 0 or 1.

  • There are no two adjacent flowers in flowerbed.

  • 0 <= n <= flowerbed.length

Explanation

  1. We can use greedy approach to solve this problem. Loop through the input array, if the current element is 1, then we skip. If the current element is 0, then we check if its left neighbor and right neighbor are also 0, then we can place the flower.

  2. Cornor case is the first and last element. If we are on the first element, we only check the right neighbor. If we are on the last element, then we only check the left neighbor.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func canPlaceFlowers(flowerbed []int, n int) bool {
    if n == 0 { return true }

    for i := range flowerbed {
        if flowerbed[i] == 1 { continue }

        if (i == 0 || flowerbed[i-1] == 0) && (i+1 == len(flowerbed) || flowerbed[i+1] == 0) {
            flowerbed[i] = 1;
            n -= 1
        }

        if n == 0 { return true }
    }

    return false
}

Populating Next Right Pointers in Each Node II

Given a binary tree

1
2
3
4
5
6
struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

  • You may only use constant extra space.

  • Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

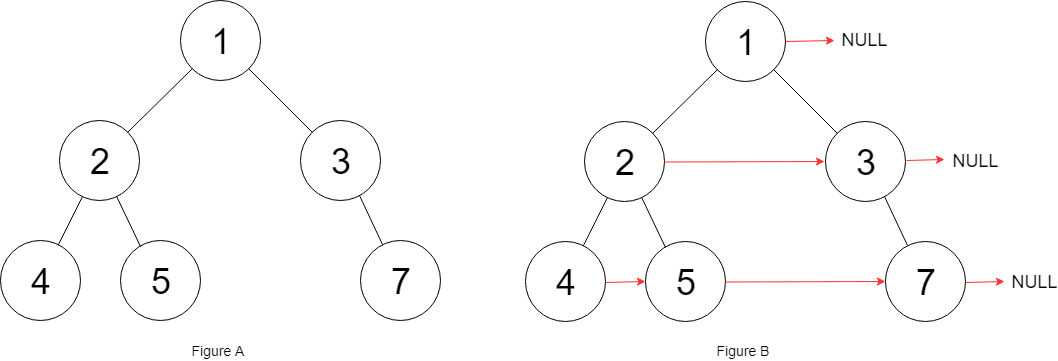
Populating-Next-Right-Pointers-in-Each-Node-II

1
2
3
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

  • The number of nodes in the given tree is less than 6000.

  • -100 <= node.val <= 100

Explanation

  1. This solution uses O(1) space and it is iterating level by level. First, we create a dummy list that is used to pointing to each level’s element before the first element. We create a cur pointer initially points to dummy and it is used to connect the current level’s element. First, if the left subnode exists, cur.next connects it, then iterate cur = cur.next. If the right subnode exists, cur.next connects it, then iterate cur = cur.next. Now, the root’s left and right subnodes are connected. Then, we move root to the right. After we move, if root is not exist, then it means we finish connecting to current root node’s sub node. We then reset root to dummy’s next node, cur reset pointing to dummy, and we set dummy’s next to null because we want the cur pointer’s next to NULL so that we can use cur.next to point to the first element in the next level.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    res := root
    dummy := &Node{}
    cur := dummy

    for root != nil {
        if root.Left != nil {
            cur.Next = root.Left
            cur = cur.Next
        }
        if root.Right != nil {
            cur.Next = root.Right
            cur = cur.Next
        }
        root = root.Next
        if root == nil {
            root = dummy.Next
            dummy.Next = nil
            cur = dummy
        }
    }

    return res
}

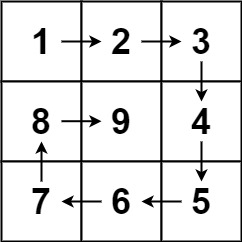
Spiral Matrix II

Given a positive integer n, generate an n x n matrix filled with elements from 1 to n^2 in spiral order.

Example 1:

Spiral-Matrix-II

1
2
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

Example 2:

1
2
Input: n = 1
Output: [[1]]

Constraints:

  • 1 <= n <= 20

Explanation

  1. Similar to 54. Spiral Matrix, we create top, right, bottom, left variables. Then create a counter starts from 1, fill the matrix. When top == bottom or left == right, since it’s a square matrix, we check if input n is an odd number or not. If it’s event, then we are done. If it’s odd, there’s a middle element, and the middle element position will be matrix[n/2][n/2], so we fill it with the counter. Finally return the filled matrix.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
func generateMatrix(n int) [][]int {
    res := make([][]int, n)
    for i := range res { res[i] = make([]int, n) }
    if n <= 0 { return res }

    top := 0
    right := len(res[0]) - 1
    bottom := len(res) - 1
    left := 0

    counter := 1
    for top < bottom && left < right {
        for i := left; i < right; i++ {
            res[top][i] = counter
            counter += 1
        }
        for i := top; i < bottom; i++ {
            res[i][right] = counter
            counter += 1
        }
        for i := right; i > left; i-- {
            res[bottom][i] = counter
            counter += 1
        }
        for i := bottom; i > top; i-- {
            res[i][left] = counter
            counter += 1
        }
        top += 1
        right -= 1
        bottom -= 1
        left += 1
    }

    if n % 2 == 1 {
        res[n/2][n/2] = counter
    }

    return res
}

Week 2: December 8th - December 14th

Missing Ranges

You are given an inclusive range [lower, upper] and a sorted unique integer array nums, where all elements are in the inclusive range.

A number x is considered missing if x is in the range [lower, upper] and x is not in nums.

Return the smallest sorted list of ranges that cover every missing number exactly. That is, no element of nums is in any of the ranges, and each missing number is in one of the ranges.

Each range [a,b] in the list should be output as:

  • "a->b" if a != b

  • "a" if a == b

Example 1:

1
2
3
4
5
6
7
Input: nums = [0,1,3,50,75], lower = 0, upper = 99
Output: ["2","4->49","51->74","76->99"]
Explanation: The ranges are:
[2,2] --> "2"
[4,49] --> "4->49"
[51,74] --> "51->74"
[76,99] --> "76->99"

Example 2:

1
2
3
Input: nums = [], lower = 1, upper = 1
Output: ["1"]
Explanation: The only missing range is [1,1], which becomes "1".

Example 3:

1
2
3
Input: nums = [], lower = -3, upper = -1
Output: ["-3->-1"]
Explanation: The only missing range is [-3,-1], which becomes "-3->-1".

Example 4:

1
2
3
Input: nums = [-1], lower = -1, upper = -1
Output: []
Explanation: There are no missing ranges since there are no missing numbers.

Example 5:

1
2
Input: nums = [-1], lower = -2, upper = -1
Output: ["-2"]

Constraints:

  • -10^9 <= lower <= upper <= 10^9

  • 0 <= nums.length <= 10^0

  • lower <= nums[i] <= upper

  • All the values of nums are unique.

Explanation

  1. We can use brute force to solve this problem. First initialize a counter cnt = lower. Loop through the array, if cnt is less than nums[i]. Then we can add the range [cnt, nums[i]-1] to the result list. Each iteration, we update cnt = nums[i] + 1. Outside the loop, we compare cnt with upper. If cnt is greater than upper that means the last element in the array is equal to upper so we can just return the result list. Else, that means the last element in the array is smaller than upper, so we add the range [cnt, upper] into the result list and return the list.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    void helper(List<String> res, int left, int right) {
        if (left == right) res.add(String.valueOf(left));
        else res.add(left + "->" + right);
    }

    public List<String> findMissingRanges(int[] nums, int lower, int upper) {
        List<String> res = new ArrayList<>();

        int cnt = lower;
        for (int i = 0; i < nums.length; i++) {
            if (cnt < nums[i]) helper(res, cnt, nums[i]-1);
            cnt = nums[i] + 1;
        }

        if (cnt <= upper) {
            helper(res, cnt, upper);
        }

        return res;
    }
}

Pairs of Songs With Total Durations Divisible by 60

You are given a list of songs where the ith song has a duration of time[i] seconds.

Return the number of pairs of songs for which their total duration in seconds is divisible by 60. Formally, we want the number of indices i, j such that i < j with (time[i] + time[j]) % 60 == 0.

Example 1:

1
2
3
4
5
6
Input: time = [30,20,150,100,40]
Output: 3
Explanation: Three pairs have a total duration divisible by 60:
(time[0] = 30, time[2] = 150): total duration 180
(time[1] = 20, time[3] = 100): total duration 120
(time[1] = 20, time[4] = 40): total duration 60

Example 2:

1
2
3
Input: time = [60,60,60]
Output: 3
Explanation: All three pairs have a total duration of 120, which is divisible by 60.

Constraints:

  • 1 <= time.length <= 6 * 10^4

  • 1 <= time[i] <= 500

Hint 1:

We only need to consider each song length modulo 60.

Hint 2:

We can count the number of songs with (length % 60) equal to r, and store that in an array of size 60.

Explanation

  1. We can create an array of size 60, arr[i] represents the number of times we visited element i. If the current element is 20, then the target element is 60 - 20 = 40, the result will increase arr[40]. Each element we can module it by 60 since if element is 20 or 80, their target element is 40.

  2. Special case is when current element is 60, we module it by 60, then it means current element is 0. Its target element is 60 - 0 = 60, and arr[60] is out of bound. Actually every element is in the range [0, 59] since we module each element by 60, so 0’s target element is also 0. So we can use (60 - t) % 60 as the target element.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
func numPairsDivisibleBy60(time []int) int {
    res := 0
    arr := make([]int, 60)

    for _, t := range time {
        t %= 60
        res += arr[(60 - t) % 60]
        arr[t] += 1
    }

    return res
}

Binary Search Tree Iterator

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

  • BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.

  • boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.

  • int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1

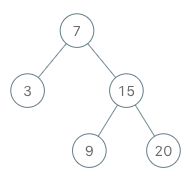
Binary Search Tree Iterator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

Constraints:

  • The number of nodes in the tree is in the range [1, 10^5].

  • 0 <= Node.val <= 10^6

  • At most 10^5 calls will be made to hasNext, and next.

Follow up:

  • Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

Explanation

  1. In the constructor, we can use in-order traversal iterative way to store the left child elements into a stack.

  2. In the hasNext function, we can check if stack is empty. If not empty, then return true.

  3. In the next function, we can return the pop node element. Also, we check if that pop node has right child, if it has right child, then we think of that right child is the root, and we push that “root” and all its left nodes to the stack like we did in the step 1.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
type BSTIterator struct {
    St []*TreeNode
}


func Constructor(root *TreeNode) BSTIterator {
    st := make([]*TreeNode, 0)
    for root != nil {
        st = append(st, root)
        root = root.Left
    }
    return BSTIterator{st}
}


func (this *BSTIterator) Next() int {
    top := this.St[len(this.St)-1]
    this.St = this.St[:len(this.St)-1]
    p := top.Right
    for p != nil {
        this.St = append(this.St, p)
        p = p.Left
    }
    return top.Val
}


func (this *BSTIterator) HasNext() bool {
    return len(this.St) > 0
}


/**
 * Your BSTIterator object will be instantiated and called as such:
 * obj := Constructor(root);
 * param_1 := obj.Next();
 * param_2 := obj.HasNext();
 */

Valid Mountain Array

Given an array of integers arr, return true if and only if it is a valid mountain array.

Recall that arr is a mountain array if and only if:

  • arr.length >= 3

  • There exists some i with 0 < i < arr.length - 1 such that:

    • arr[0] < arr[1] < ... < arr[i - 1] < A[i]

    • arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

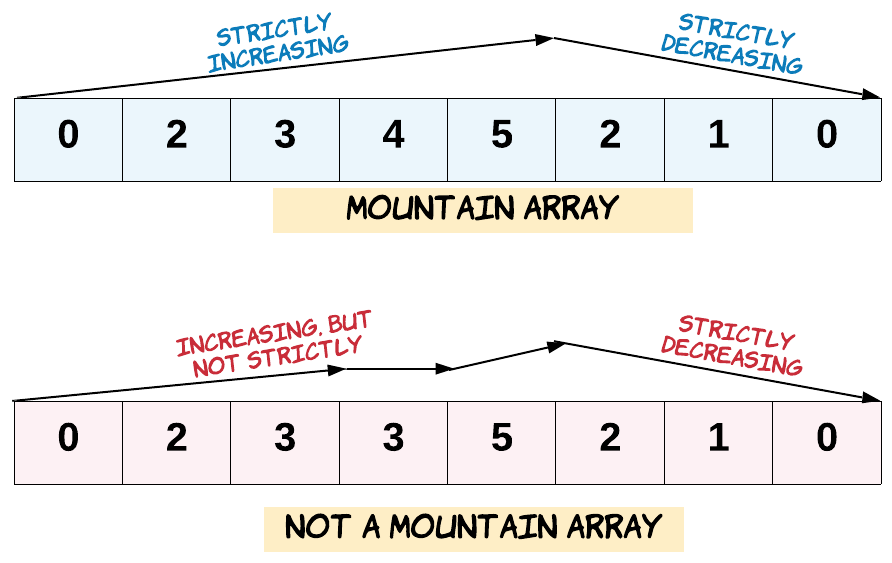
Valid Mountain Array

Example 1:

1
2
Input: arr = [2,1]
Output: false

Example 2:

1
2
Input: arr = [3,5,5]
Output: false

Example 3:

1
2
Input: arr = [0,3,2,1]
Output: true

Constraints:

  • 1 <= arr.length <= 10^4

  • 0 <= arr[i] <= 10^4

Hint 1:

It’s very easy to keep track of a monotonically increasing or decreasing ordering of elements. You just need to be able to determine the start of the valley in the mountain and from that point onwards, it should be a valley i.e. no mini-hills after that. Use this information in regards to the values in the array and you will be able to come up with a straightforward solution.

Explanation

  1. A valid mountain array can only has exactly one increasing and one decreasing Also, we see increasing first, then decreasing.

  2. Loop through the array. If arr[i-1] < arr[i] then we update increasing = true. Also we check if decreasing is true or not. If decreasing is also true that means we see decreasing in front increasing so we return false. If arr[i-1] > arr[i], then we just update decreasing = true. Else if arr[i-1] == arr[i], then we can return false immediately.

  3. At the end, if increasing and decreasing both are true, then we return true, else return false.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func validMountainArray(arr []int) bool {
    if len(arr) < 3 { return false }
    increasing, decreasing := false, false

    for i := 1; i < len(arr); i++ {
        if arr[i-1] < arr[i] {
            increasing = true
            if decreasing == true { return false }
        } else if arr[i-1] > arr[i] {
            decreasing = true
        } else {
            return false
        }
    }

    return increasing && decreasing
}

Remove Duplicates from Sorted Array II

Given a sorted array nums, remove the duplicates in-place such that duplicates appeared at most twice and return the new length.

Do not allocate extra space for another array; you must do this by modifying the input array in-place with O(1) extra memory.

Clarification:

Confused why the returned value is an integer, but your answer is an array?

Note that the input array is passed in by reference, which means a modification to the input array will be known to the caller.

Internally you can think of this:

1
2
3
4
5
6
7
8
// nums is passed in by reference. (i.e., without making a copy)
int len = removeDuplicates(nums);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

Example 1:

1
2
3
Input: nums = [1,1,1,2,2,3]
Output: 5, nums = [1,1,2,2,3]
Explanation: Your function should return length = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively. It doesn't matter what you leave beyond the returned length.

Example 2:

1
2
3
Input: nums = [0,0,1,1,1,1,2,3,3]
Output: 7, nums = [0,0,1,1,2,3,3]
Explanation: Your function should return length = 7, with the first seven elements of nums being modified to 0, 0, 1, 1, 2, 3 and 3 respectively. It doesn't matter what values are set beyond the returned length.

Constraints:

  • 0 <= nums.length <= 3 * 10^4

  • -10^4 <= nums[i] <= 10^4

  • nums is sorted in ascending order.

Explanation

  1. First, we start from the third element because we can have two duplicated, so it doesn’t matter if the first two elements are the same or not. We also use currentPointer and fastPointer technique to solve this problem. Initially, the current pointer and the fastPointer are pointing at the third element. The currentPointer is used to store the next valid element, the fastPointer is used to iterate the input array until it hits the end.

  2. We can compare the fast pointer element with the currentPointer-1 index element and currentPointer-2 index element, if they are the same, then it means there are already two same elements before the currentPointer index. Else, we can set the currentPointer index’s value to the fastPointer’s pointing value.

Solution

1
2
3
4
5
6
7
8
9
10
func removeDuplicates(nums []int) int {
    if len(nums) <= 2 { return len(nums) }
    curPtr := 2
    for fastPtr := 2; fastPtr < len(nums); fastPtr++ {
        if nums[curPtr-2] == nums[fastPtr] && nums[curPtr-1] == nums[fastPtr] { continue }
        nums[curPtr] = nums[fastPtr]
        curPtr += 1
    }
    return curPtr
}

Smallest Subtree with all the Deepest Nodes

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is tree consisting of that node, plus the set of all descendants of that node.

Note: This question is the same as 1123: https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/

Example 1:

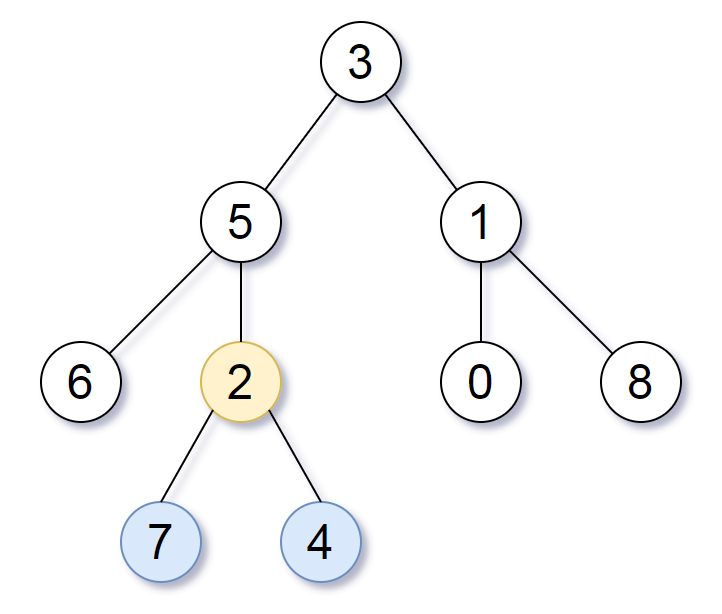
Smallest Subtree with all the Deepest Nodes

1
2
3
4
5
Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
The nodes coloured in blue are the deepest nodes of the tree.
Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:

1
2
3
Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:

1
2
3
Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

Constraints:

  • The number of nodes in the tree will be in the range [1, 500].

  • 0 <= Node.val <= 500

  • The values of the nodes in the tree are unique.

Explanation 1

  1. If the left child and right child’s height are the same, then the smallest subtree with all the deepest nodes (result node) must be the root node. Else left child height is higher than the right child height, then the result node will be inside the left subtree, so we recursively call the main function with the left child node; else if right child height is higher, then the result node will be in the right subtree, so we call the main function with the right child node.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func subtreeWithAllDeepest(root *TreeNode) *TreeNode {
    leftDepth := helper(root.Left)
    rightDepth := helper(root.Right)
    if leftDepth == rightDepth {
        return root
    } else if leftDepth < rightDepth {
        return subtreeWithAllDeepest(root.Right)
    } else {
        return subtreeWithAllDeepest(root.Left)
    }
}

func helper(root *TreeNode) int {
    if root == nil { return 0 }
    return 1 + max(helper(root.Left), helper(root.Right))
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Explanation 2

  1. There are many duplicate computation from the above solution, we can improve it. Instead of just returning the height in the helper function, we return the height and the smallest subtree with all the deepest nodes, in other words, we return the height and the result node.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func subtreeWithAllDeepest(root *TreeNode) *TreeNode {
    _, res := helper(root)
    return res
}

func helper(root *TreeNode) (int, *TreeNode) {
    if root == nil { return 0, new(TreeNode) }

    leftDepth, leftSubtreeWithAllDeepest := helper(root.Left)
    rightDepth, rightSubtreeWithAllDeepest := helper(root.Right)

    if leftDepth == rightDepth {
        return 1 + leftDepth, root
    } else if leftDepth < rightDepth {
        return 1 + rightDepth, rightSubtreeWithAllDeepest
    } else {
        return 1 + leftDepth, leftSubtreeWithAllDeepest
    }
}

Burst Balloons

Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get nums[left] * nums[i] * nums[right] coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.

Find the maximum coins you can collect by bursting the balloons wisely.

Note:

  • You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.

  • 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100

Example:

1
2
3
4
Input: [3,1,5,8]
Output: 167
Explanation: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
             coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

Explanation

  1. We can use dynamic programming to solve this problem.

  2. Dynamic state is dp[left][right], it means the maximum coins that can get between left+1 to right-1 inclusive. We will add 1 to the beginning and the end of the array as the updated array. So the dynamic result will be dp[0][n-1], n is the number of elements in the updated array. If the input array is [2, 5, 3], then the udpated array will be [1, 2, 5, 3, 1]. We will find dp[0][5-1].

  3. Dynamic init will be all dp[left][right] be zero.

  4. If input array is [2, 5, 3], updated array is [1, 2, 5, 3, 1], we will find dp[left=0][right=5-1=4]. If i=5, and it is the last element we burst, then its coin will be 1*5*1; 2 and 3 are already burst before 5, so we will add their coins, which are 1*2*5 and 5*3*1. In other words, add dp[left][i] and dp[i][right]. Remember the dynamic state is dp[left][right], it means the maximum coins that can get between left+1 to right-1 inclusive. So, our dynamic function is dp[left][right] = max(dp[left][right], coins[i]*coins[left]*coins[right] + dp[left][i] + dp[i][right]).

  5. If input array has only one element, for example [2], then the updated array will have length 3, which is [1, 2, 1]. left and right will have max distance 2 (rightIndex - leftIndex), and the result will be dp[0, 2]. Also, 2 is also the minimum distance. If input array is [2, 3], then updated array is [1, 2, 3, 1], which has max distance 3 between left and right. At the beginning, we can first find out all the result of the smallest distance dp, in other words, the smallest sub array result, then we find the larger distance sub array result. So we will find subarray [1, 2, 3] and subarray [2, 3, 1], then find the whole array [1, 2, 3, 1]. If the last ballon we burst is 2, then we have coin 1*2*1, and 3 is already burst before 2, so we have coin 2*3*1, which is the result of the subarray dp[2, 3, 1], so the totoal coin is 1*2*1+2*3*1. If the last ballon we burst is 3, then we have coin 1*3*1, and 2 is already burst before 3, so we have coin 1*2*3, which is the result of the subarray dp[1, 2, 3], so the total coin is 1*3*1+1*2*3. At the end, we compare both result and take the maximum as the final result for the updated array [1, 2, 3, 1].

  6. So, we first loop through distance, then loop through the left starting point, and right will be right = left + distance. Then, we loop through i, which is left < i < right, to choose which element is the last element we burst. Then we use our dynamic function dp[left][right] = max(dp[left][right], coins[i]*coins[left]*coins[right] + dp[left][i] + dp[i][right]) to update the solution.

  7. At the end, we return the dynamic result dp[0][n-1]. If input array is [2], updated array is [1, 2, 1], dynamic result will be dp[0][3-1].

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func maxCoins(nums []int) int {
    coins := make([]int, len(nums) + 2)
    n := 1

    for _, c := range nums {
        coins[n] = c
        n += 1
    }
    coins[0], coins[n] = 1, 1
    n += 1

    maxCoin := make([][]int, n)
    for i := range maxCoin {
        maxCoin[i] = make([]int, n)
    }

    for dist := 2; dist < n; dist++ {
        for left := 0; left + dist < n; left++ {
            right := left + dist
            for i := left + 1; i <= right - 1; i++ {
                maxCoin[left][right] = max(maxCoin[left][right],
                                           coins[i] * coins[left] * coins[right] + maxCoin[left][i] + maxCoin[i][right])
            }
        }
    }

    return maxCoin[0][n-1]
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Palindrome Partitioning

Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.

A palindrome string is a string that reads the same backward as forward.

Example 1:

1
2
Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]

Example 2:

1
2
Input: s = "a"
Output: [["a"]]

Constraints:

  • 1 <= s.length <= 16

  • s contains only lowercase English letters.

Explanation

  1. First create a function to check whether a string is palindrome.

  2. We can use backtracking to find all combination, if a substring is palindrome, then we start from the next character of the substring and check. For example, “abac”, when we check “aba” is a palindrome, then we check start from “c”.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func partition(s string) [][]string {
    res := make([][]string, 0)
    builder := make([]string, 0)

    helper(s, 0, builder, &res)

    return res
}

func helper(s string, start int, builder []string, res*[][]string) {
    if start == len(s) {
        temp := make([]string, len(builder))
        copy(temp, builder)
        *res = append(*res, temp)
    } else {
        for i := start; i < len(s); i++ {
            if isPalidrome(s, start, i) == true {
                builder = append(builder, s[start:i+1])
                helper(s, i+1, builder, res)
                builder = builder[:len(builder)-1]
            }
        }
    }
}

func isPalidrome(s string, start int, end int) bool {
    for start < end {
        if s[start] != s[end] {
            return false
        }
        start += 1
        end -= 1
    }

    return true
}

Week 3: December 15th - December 21st

Plus One Linked List

Given a non-negative integer represented as a linked list of digits, plus one to the integer.

The digits are stored such that the most significant digit is at the head of the list.

Example 1:

1
2
Input: head = [1,2,3]
Output: [1,2,4]

Example 2:

1
2
Input: head = [0]
Output: [1]

Constraints:

  • The number of nodes in the linked list is in the range [1, 100].

  • 0 <= Node.val <= 9

  • The number represented by the linked list does not contain leading zeros except for the zero itself.

Explanation

  1. First, we create a dummy node and connect it before the head.

  2. Then we find the right most digit that is not equal to 9, initially this non-nine node points to dummy.

  3. Increase the right most non-nine node’s value by 1, and set all its following node to value 0.

  4. If the non-nine node is still points to dummy, that means the link list’s all digits are 0, so we return dummy. Else, we return dummy.next which is the original head.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode plusOne(ListNode head) {
        ListNode dummy = new ListNode();
        dummy.next = head;
        ListNode nonNine = dummy;

        while (head != null) {
            if (head.val != 9) nonNine = head;
            head = head.next;
        }

        nonNine.val += 1;
        ListNode temp = nonNine.next;
        while (temp != null) {
            temp.val = 0;
            temp = temp.next;
        }

        if (nonNine == dummy) {
            return dummy;
        } else {
            return dummy.next;
        }
    }
}

Squares of a Sorted Array

Given an integer array nums sorted in non-decreasing order, return an array of the squares of each number sorted in non-decreasing order.

Example 1:

1
2
3
4
Input: nums = [-4,-1,0,3,10]
Output: [0,1,9,16,100]
Explanation: After squaring, the array becomes [16,1,0,9,100].
After sorting, it becomes [0,1,9,16,100].

Example 2:

1
2
Input: nums = [-7,-3,2,3,11]
Output: [4,9,9,49,121]

Constraints:

  • 1 <= nums.length <= 10^4

  • -10^4 <= nums[i] <= 10^4

  • nums is sorted in non-decreasing order.

Explanation 1

  1. We can use two pointers to solve this problem. For negative number, the larger negative number has smaller square. For non-negative number, the smaller positive number has the smaller square. First, we need to find the first non-negative number’s index, then we use a right pointer points to this index, and use a left pointer points to index at right - 1. We will compare nums[left] and nums[right], if nums[left] is smaller, then we append it into the result array and decrease left; else we append nums[right] into the array and increase right.

  2. Corner case are if the first number of the input array is equal or greater than 0, then we simply one loop and each iteration we put the square of the iterated number into the result array. If the last number of the input array is negative, then we simply loop from right to left and each iteration, we put the iterated number’s square into the array.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
func sortedSquares(nums []int) []int {
    res := make([]int, len(nums))
    idx := 0
    left, right := 0, 0
    if nums[0] >= 0 {
        right = 0
        left = -1
    } else if nums[len(nums)-1] < 0 {
        left = len(nums)-1
        right = len(nums)
    } else {
        right = firstNonNegative(nums)
        left = right - 1
    }

    for left >= 0 && right < len(nums) {
        leftRes := nums[left] * nums[left]
        rightRes := nums[right] * nums[right]
        if leftRes < rightRes {
            res[idx] = leftRes
            left -= 1
        } else {
            res[idx] = rightRes
            right += 1
        }
        idx += 1
    }

    for left >= 0 {
        res[idx] = nums[left] * nums[left]
        idx += 1
        left -= 1
    }

    for right < len(nums) {
        res[idx] = nums[right] * nums[right]
        idx += 1
        right += 1
    }

    return res
}

func firstNonNegative(nums []int) int {
    left, right := 0, len(nums) - 1

    for left < right {
        mid := left + (right - left) / 2
        if nums[mid] < 0 {
            left = mid + 1
        } else {
            right = mid
        }
    }

    return left
}

Explanation 2

  1. We can also start to find the larger square first. For negative number, the larger square is at index 0 so we use left pointer points at 0. For non-negative number, the larger square is at the last index of the array so we use right pointer points at last index of the array. If the right square (nums[right] * nums[right]) is larger, then we prepend the right square at end of the result array and decrease right pointer. Else if the left square (nums[left] * nums[left]) is larger, then we prepend the left square and increase left pointer.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func sortedSquares(nums []int) []int {
    res := make([]int, len(nums))
    left, right := 0, len(nums) - 1

    for idx := len(nums)-1; idx >= 0; idx-- {
        leftRes := nums[left] * nums[left]
        rightRes := nums[right] * nums[right]
        if leftRes < rightRes {
            res[idx] = rightRes
            right -= 1
        } else {
            res[idx] = leftRes
            left += 1
        }
    }

    return res
}

Validate Binary Search Tree

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

  • The left subtree of a node contains only nodes with keys less than the node’s key.

  • The right subtree of a node contains only nodes with keys greater than the node’s key.

  • Both the left and right subtrees must also be binary search trees.

Example 1:

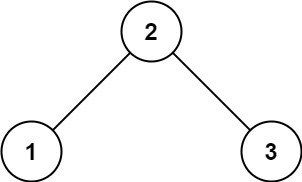
Validate Binary Search Tree

1
2
Input: root = [2,1,3]
Output: true

Example 2:

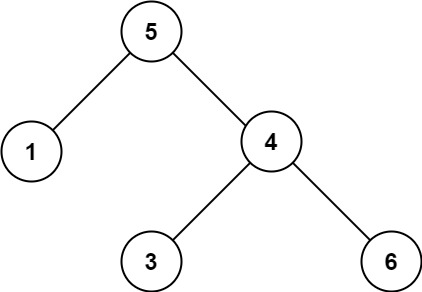
Validate Binary Search Tree

1
2
3
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.

Constraints:

  • The number of nodes in the tree is in the range [1, 10^4].

  • -2^31 <= Node.val <= 2^31 - 1

Explanation

  1. We can solve this problem using in-order traversal.

  2. When we are iterating, we can compare the current node’s value with previous node’s value. If previous node’s value is greater than or equal to current iterated node’s value, we can return false immediately.

  3. We can initialize the previouse node value as null.

  4. In the helper function, if current node is null, we need to return true.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isValidBST(root *TreeNode) bool {
    pre := &TreeNode{}
    pre = nil
    // var pre *TreeNode = nil
    return helper(root, &pre)
}

func helper(root *TreeNode, pre **TreeNode) bool {
    if root == nil { return true }

    leftRes := helper(root.Left, pre)

    if leftRes == false { return false }
    if *pre != nil && (*pre).Val >= root.Val { return false }
    *pre = root

    return helper(root.Right, pre)
}

4Sum II

Given four lists A, B, C, D of integer values, compute how many tuples (i, j, k, l) there are such that A[i] + B[j] + C[k] + D[l] is zero.

To make problem a bit easier, all A, B, C, D have same length of N where 0 ≤ N ≤ 500. All integers are in the range of -2^28 to 2^28 - 1 and the result is guaranteed to be at most 2^31 - 1.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input:
A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]

Output:
2

Explanation:
The two tuples are:
1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> A[1] + B[1] + C[0] + D[0] = 2 + (-1) + (-1) + 0 = 0

Explanation

  1. Similar to Two Sum, in Two Sum, we iterate the list and push elements as key into a HashMap, its index as value. Then loop the list again to find the target, which is 0-arr[i], from the HashMap.

  2. Now if we iterate 4 lists, then we need n4 runtime. We can reduce it to n2 by iterating every elements of ListA and ListB. Push all the sums as key to a HashMap and value will be the sums’ frequency.

  3. Next, we iterate every elements of ListC and ListD, calculate the sums, target will be 0-sum, from the HashMap, accumulate the frequency to result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func fourSumCount(A []int, B []int, C []int, D []int) int {
    res := 0
    hm := make(map[int]int)

    for _, a := range A {
        for _, b := range B {
            sum := a + b
            hm[sum]++
        }
    }

    for _, c := range C {
        for _, d := range D {
            target := -(c + d)
            res += hm[target]
        }
    }

    return res
}

Increasing Triplet Subsequence

Given an integer array nums, return true if there exists a triple of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k]. If no such indices exists, return false.

Example 1:

1
2
3
Input: nums = [1,2,3,4,5]
Output: true
Explanation: Any triplet where i < j < k is valid.

Example 2:

1
2
3
Input: nums = [5,4,3,2,1]
Output: false
Explanation: No triplet exists.

Example 3:

1
2
3
Input: nums = [2,1,5,0,4,6]
Output: true
Explanation: The triplet (3, 4, 5) is valid because nums[3] == 0 < nums[4] == 4 < nums[5] == 6.

Constraints:

  • 1 <= nums.length <= 105

  • -2^31 <= nums[i] <= 2^31 - 1

Follow up: Could you implement a solution that runs in O(n) time complexity and O(1) space complexity?

Explanation 1

  1. We create an array dp[i], which means before nums[i], the number of elements that are less than nums[i]. We initialize dp[] has the same length as nums[] and all the values initialize to 1.

  2. For every nums[i], we loop every element (nums[j]) before nums[i], if nums[j] < nums[i], then we update dp[i] = dp[j] + 1.

  3. If dp[i] == 3, that means there are two elements before it are less than nums[i], so we return true. Else after checking every element, we return false.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func increasingTriplet(nums []int) bool {
    dp := make([]int, len(nums))
    for i := range dp {
        dp[i] = 1
    }

    for i := 0; i < len(nums); i++ {
        for j := 0; j < i; j++ {
            if nums[j] < nums[i] {
                dp[i] = max(dp[i], dp[j] + 1)
            }
            if dp[i] == 3 { return true }
        }
    }

    return false
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Explanation 2

  1. We want to three numbers that stisify m1 < m2 < nums[i]. First, we create two variables m1 and m2 that equals to maximum integer. Next, we loop through every element in the array, if nums[i] <= m1, then we update m1 = nums[i]; else if nums[i] > m1 && nums[i] <= m2, then we udpate m2; else if m1 < nums[i] && m2 < nums[i], then we return true. After looping all elements, if we don’t return true, then we return false.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func increasingTriplet(nums []int) bool {
    min1, min2 := math.MaxInt32, math.MaxInt32

    for _, num := range nums {
        if num <= min1 {
            min1 = num
        } else if num <= min2 {
            min2 = num
        } else {
            return true
        }
    }

    return false
}

Explanation 3

  1. We create two arrays forward[] and backward[]. forward[i] means the minimum elements that are from index 0 to index i (inclusive). backward[i] means the maximum elements that are from index i to the last index (inclusive). We initialize forward[0] = nums[0] and loop from index 1 to last index, update forward[i]. Next, we initialize backward[nums.length-1] = nums[nums.length-1], loop from index nums.length-2 to index 0, update backward[i]. After we updating both forward[] and backward[], we loop nums[] from index 0 to last index. If forward[i] < nums[i] && nums[i] < backward[i], we return true. Else after finish looping, we return false.

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func increasingTriplet(nums []int) bool {
    forward := make([]int, len(nums))
    backward := make([]int, len(nums))

    forward[0] = nums[0]
    for i := 1; i < len(nums); i++ {
        if forward[i-1] < nums[i] {
            forward[i] = forward[i-1]
        } else {
            forward[i] = nums[i]
        }
    }

    backward[len(nums)-1] = nums[len(nums)-1]
    for i := len(nums)-2; i >= 0; i-- {
        if backward[i+1] > nums[i] {
            backward[i] = backward[i+1]
        } else {
            backward[i] = nums[i]
        }
    }

    for i := 0; i < len(nums); i++ {
        if forward[i] < nums[i] && nums[i] < backward[i] {
            return true
        }
    }

    return false
}

Cherry Pickup II

Given a rows x cols matrix grid representing a field of cherries. Each cell in grid represents the number of cherries that you can collect.

You have two robots that can collect cherries for you, Robot #1 is located at the top-left corner (0,0) , and Robot #2 is located at the top-right corner (0, cols-1) of the grid.

Return the maximum number of cherries collection using both robots by following the rules below:

  • From a cell (i,j), robots can move to cell (i+1, j-1) , (i+1, j) or (i+1, j+1).

  • When any robot is passing through a cell, It picks it up all cherries, and the cell becomes an empty cell (0).

  • When both robots stay on the same cell, only one of them takes the cherries.

  • Both robots cannot move outside of the grid at any moment.

  • Both robots should reach the bottom row in the grid.

Example 1:

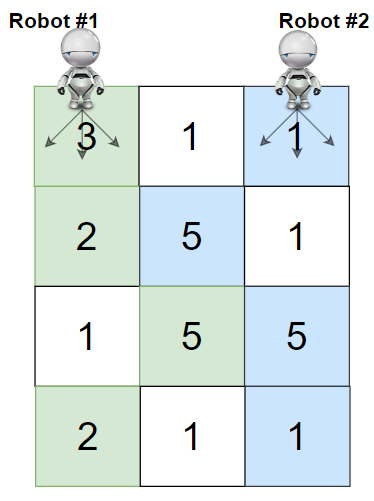
Cherry Pickup II

1
2
3
4
5
6
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.

Example 2:

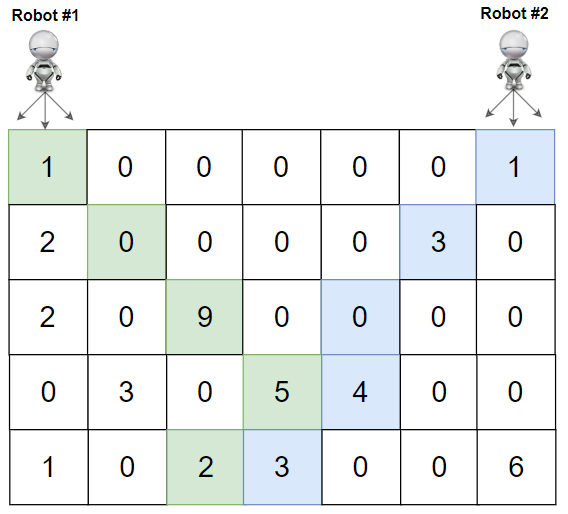
Cherry Pickup II

1
2
3
4
5
6
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.

Example 3:

1
2
Input: grid = [[1,0,0,3],[0,0,0,3],[0,0,3,3],[9,0,3,3]]
Output: 22

Example 4:

1
2
Input: grid = [[1,1],[1,1]]
Output: 4

Constraints:

  • rows == grid.length

  • cols == grid[i].length

  • 2 <= rows, cols <= 70

  • 0 <= grid[i][j] <= 100

Hint 1:

Use dynammic programming, define DP[i][j][k]: The maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively.

Explanation

  1. We can use dynamic programming to solve this problem. Dynamic state is dp[r][col1][col2] which represents the maximum cherries that both robots can take starting on the ith row, and column j and k of Robot 1 and 2 respectively. For each row, we need to check all the combinations of robot1’s column and robot2’s column and that’s why we need a 3 dimensional array dp[r][col1][col2].

  2. First, we initialize all the dp elements to -1, so dp[r][col1][col2] represents both robots cannot reach grid[r][col1] and grid[r][col2]. Dynamic init is dp[0][0][col] = grid[0][0] + grid[0][col] since both robots start from these two points.

  3. Dynamic function is dp[r][col1][col2] = max(dp[r][col1][col2], prev + grid[r][col1] + grid[r][col2]) where prev = dp[r-1][c1][c2] and col1 can be one of [c1-1, c1, c1+1], and similarlly for col2 can be one of [c2-1, c2, c2+1]. If col1 is equal to col2, then instead of prev + grid[r][col1] + grid[r][col2], we only need to plus one of them so prev + grid[r][col1] because when both robots stay on the same cell, only one of them takes the cherries. Every time we update dp[r][col1][col2], we need to keep track of the maximum result res.

  4. At the end, we return the maximum result res.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
func cherryPickup(grid [][]int) int {
    row, col := len(grid) - 1, len(grid[0]) - 1
    dir := []int{-1, 0, 1}
    dp := make([][][]int, row+1)
    for i := 0; i <= row; i++ {
        dp[i] = make([][]int, col+1)
        for j := 0; j <= col; j++ {
            dp[i][j] = make([]int, col+1)
            for k := 0; k <= col; k++ {
                dp[i][j][k] = -1;
            }
        }
    }

    dp[0][0][col] = grid[0][0] + grid[0][col]
    res := dp[0][0][col]

    for r := 1; r <= row; r++ {
        for c1 := 0; c1 <= col; c1++ {
            for c2 := 0; c2 <= col; c2++ {
                prev := dp[r-1][c1][c2]

                if prev >= 0 {
                    for _, d1 := range dir {
                        col1 := c1 + d1
                        for _, d2 := range dir {
                            col2 := c2 + d2

                            if inRange(col1, col) && inRange(col2, col) {
                                temp := 0
                                if col1 == col2 {
                                    temp = prev + grid[r][col1]
                                } else {
                                    temp = prev + grid[r][col1] + grid[r][col2]
                                }
                                dp[r][col1][col2] = max(dp[r][col1][col2], temp)
                                res = max(res, dp[r][col1][col2])
                            }
                        }
                    }
                }
            }
        }
    }

    return res
}

func inRange(a, col int) bool {
    return 0 <= a && a <= col
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Decoded String at Index

An encoded string S is given. To find and write the decoded string to a tape, the encoded string is read one character at a time and the following steps are taken:

  • If the character read is a letter, that letter is written onto the tape.

  • If the character read is a digit (say d), the entire current tape is repeatedly written d-1 more times in total.

Now for some encoded string S, and an index K, find and return the K-th letter (1 indexed) in the decoded string.

Example 1:

1
2
3
4
5
Input: S = "leet2code3", K = 10
Output: "o"
Explanation:
The decoded string is "leetleetcodeleetleetcodeleetleetcode".
The 10th letter in the string is "o".

Example 2:

1
2
3
4
Input: S = "ha22", K = 5
Output: "h"
Explanation:
The decoded string is "hahahaha".  The 5th letter is "h".

Example 3:

1
2
3
4
Input: S = "a2345678999999999999999", K = 1
Output: "a"
Explanation:
The decoded string is "a" repeated 8301530446056247680 times.  The 1st letter is "a".

Constraints:

  • 2 <= S.length <= 100

  • S will only contain lowercase letters and digits 2 through 9.

  • S starts with a letter.

  • 1 <= K <= 10^9

  • It’s guaranteed that K is less than or equal to the length of the decoded string.

  • The decoded string is guaranteed to have less than 2^63 letters.

Explanation

  1. If we have a decoded string like appleappleappleappleappleapple and an index like K = 24, the answer is the same if K = 4.

  2. In general, when a decoded string is equal to some word with size length repeated some number of times (such as apple with size = 5 repeated 6 times), the answer is the same for the index K as it is for the index K % size.

  3. We can use this insight by working backwards, keeping track of the size of the decoded string. Whenever the decoded string would equal some word repeated d times, we can reduce K to K % (word.length).

  4. First, find the length of the decoded string, when size is greater than or equal to K we can stop here. After, we’ll work backwards, keeping track of size: the length of the decoded string after parsing symbols S[0], S[1], ..., S[i].

  5. If we see a digit S[i], it means the size of the decoded string after parsing S[0], S[1], ..., S[i-1] will be size / Integer(S[i]). Otherwise, it will be size - 1.

  6. Corner case is size should be type long.

Source: 880. Decoded String at Index Solution

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func decodeAtIndex(S string, K int) string {
    size := 0
    i := 0
    for ; size < K; i++ {
        if S[i] >= 'A' {
            size += 1
        } else {
            size *= int(S[i] - '0')
        }
    }
    i -= 1

    for i >= 0 {
        if S[i] < 'A' {
            size /= int(S[i] - '0')
            K %= size
        } else {
            if K % size == 0 {
                return string(S[i])
            } else {
                size -= 1
            }
        }
        i -= 1
    }

    return ""
}

Smallest Range II

Given an array A of integers, for each integer A[i] we need to choose either x = -K or x = K, and add x to A[i] (only once).

After this process, we have some array B.

Return the smallest possible difference between the maximum value of B and the minimum value of B.

Example 1:

1
2
3
Input: A = [1], K = 0
Output: 0
Explanation: B = [1]

Example 2:

1
2
3
Input: A = [0,10], K = 2
Output: 6
Explanation: B = [2,8]

Example 3:

1
2
3
Input: A = [1,3,6], K = 3
Output: 3
Explanation: B = [4,6,3]

Note:

  1. 1 <= A.length <= 10000

  2. 0 <= A[i] <= 10000

  3. 0 <= K <= 10000

Explanation

  1. First, we sort the array.

  2. We want to find the smallest difference between the maximum value and minimum value in the new array, so we will try to in the original array plus K for the minimum value and subtract K for the minimum value.

  3. We can divide the original array into two half A[0: i] andA[i+1: len(A)]. In the first half array, we will plus K for every element; in the second half, we will subtract K for every element. So in the first half, the minimum value is A[0] + K and the maximum value is A[i] + K. In the second half, the minimum value is A[i+1] - K and the maximum value is A[len(A)-1] - K. Therefore, in the entire new array, the minimum value is min(A[0] + K, A[i+1] - K) and the maximum value is max(A[i] + K, A[len(A)-1] - K). So, we can iterate i and each iteration, we calculate the minimum difference.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func smallestRangeII(A []int, K int) int {
    sort.Ints(A)
    res := A[len(A)-1] - A[0]
    left, right := A[0] + K, A[len(A)-1] - K

    for i := 0; i < len(A) - 1; i++ {
        low := min(left, A[i+1] - K)
        high := max(right, A[i] + K)
        res = min(res, high - low)
    }

    return res
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Week 4: December 22nd - December 28th

Find Nearest Right Node in Binary Tree

Given the root of a binary tree and a node u in the tree, return the nearest node on the same level that is to the right of u, or return null if u is the rightmost node in its level.

Example 1:

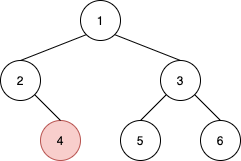
Find Nearest Right Node in Binary Tree

1
2
3
Input: root = [1,2,3,null,4,5,6], u = 4
Output: 5
Explanation: The nearest node on the same level to the right of node 4 is node 5.

Example 2:

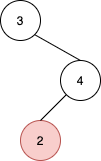
Find Nearest Right Node in Binary Tree

1
2
3
Input: root = [3,null,4,2], u = 2
Output: null
Explanation: There are no nodes to the right of 2.

Example 3:

1
2
Input: root = [1], u = 1
Output: null

Example 4:

1
2
Input: root = [3,4,2,null,null,null,1], u = 4
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [1, 10^5].

  • 1 <= Node.val <= 10^5

  • All values in the tree are distinct.

  • u is a node in the binary tree rooted at root.

Hint 1:

Use BFS, traverse the tree level by level and always push the left node first

Hint 2:

When you reach the target node, mark a boolean variable true

Hint 3:

If you meet another node in the same level after marking the boolean true, return this node.

Hint 4:

If you did not meet new nodes in the same level and started traversing a new level, return Null

Explanation

  1. We can use level-order traversal to solve this problem. When we find the target node, we can check if the current i is at the end of the current level, then we return null, else we return the next node of the queue.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode findNearestRightNode(TreeNode root, TreeNode u) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            for (int i = queue.size() - 1; i >= 0; i--) {
                TreeNode cur = queue.poll();
                if (cur.val == u.val) {
                    if (i == 0) return null;
                    else return queue.poll();
                }
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return null;
    }
}

Balanced Binary Tree

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

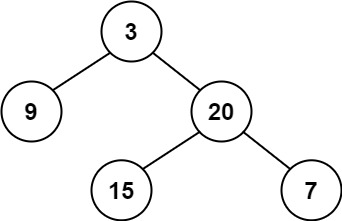
Balanced Binary Tree

1
2
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

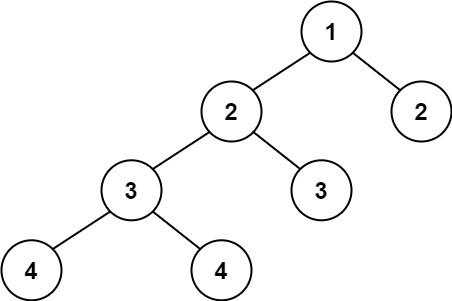
Balanced Binary Tree

1
2
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

1
2
Input: root = []
Output: true

Constraints:

  • The number of nodes in the tree is in the range [0, 5000].

  • -10^4 <= Node.val <= 10^4

Explanation

  1. This problem is very similar to 865. Smallest Subtree with all the Deepest Nodes. We need to find the left subtree’s height and right subtree’s height, then compare these two height’s difference. If the difference is less than or equal to 1, then it’s balanced, else it’s unbalanced. So this problem can be solved by using post-order traversal.

  2. It is possible that the left subtree and right subtree’s height are the same, but left subtree or right subtree is unbalanced, so we need to recursively run the main function to check if left subtree is balanced or not, and run the main function to check if the right subtree is balanced or not.

  3. Above solution requires us to calculate the height of the subtree multiple times. To improve time complexity, instead of just returning the height in the helper function, we can return the height and a boolean value to indicate if the subtree is balanced or not. So, if the left subtree is unbalanced, then we can return 1 + leftSubtreeHeight and false immediately and skip checking right subtree, vice versa. If left subtree and right subtree are balanced, then we can return 1 + max(leftHeight, rightHeight) and true.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isBalanced(root *TreeNode) bool {
    _, res := helper(root)
    return res
}

func helper(root *TreeNode) (int, bool) {
    if root == nil { return 0, true }
    
    leftDepth, isLeftBalanced := helper(root.Left)
    if !isLeftBalanced { return 1 + leftDepth, false }
    
    rightDepth, isRightBalanced := helper(root.Right)
    if !isRightBalanced { return 1 + rightDepth, false }
    
    if math.Abs(float64(leftDepth - rightDepth)) > 1 { return 1 + rightDepth, false }
    
    return 1 + max(leftDepth, rightDepth), true
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Next Greater Element III

Given a positive integer n, find the smallest integer which has exactly the same digits existing in the integer n and is greater in value than n. If no such positive integer exists, return -1.

Note that the returned integer should fit in 32-bit integer, if there is a valid answer but it does not fit in 32-bit integer, return -1.

Example 1:

1
2
Input: n = 12
Output: 21

Example 2:

1
2
Input: n = 21
Output: -1

Constraints:

  • 1 <= n <= 2^31 - 1

Explanation

  1. If the input is 12443322, then the result should be 13222344. We observe that the reason the number becomes large is the first 2 change to be 3. Also, after this position, the rest of the numbers becomes from decreasing to increasing.

  2. The reason we choose to update the first 2 is from the right to left, 2 is the first number less than its right number. If the whole input number is decreasing order (i.e. 443322), then we can’t reorder it to get the larger number, so we return -1.

  3. The reason we choose 3 to swap with the first 2 is from the right to left, 3 is the first number greater than 2.

  4. After we swap, we need to sort or reverse all the digits after the first 2, so they become increasing.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func nextGreaterElement(n int) int {
    str := []rune(strconv.Itoa(n))
    i := len(str) - 1
    for ; i > 0; i-- {
        if str[i] > str[i-1] {
            break
        }
    }
    
    if i == 0 { return - 1 }
    
    for j := len(str) - 1; j > i - 1; j-- {
        if str[j] > str[i-1] {
            str[i-1], str[j] = str[j], str[i-1]
            break
        }
    }
    
    str = reverse(str, i, len(str)-1)
    
    num, _ := strconv.Atoi(string(str))
    if num > math.MaxInt32 {
        return -1
    } else {
        return num
    }
}

func reverse(str []rune, left, right int) []rune {
    for left < right {
        str[left], str[right] = str[right], str[left]
        left += 1
        right -= 1
    }
    return str
}

Swap Nodes in Pairs

Given a linked list, swap every two adjacent nodes and return its head.

You may not modify the values in the list’s nodes. Only nodes itself may be changed.

Example 1:

Swap Nodes in Pairs

1
2
Input: head = [1,2,3,4]
Output: [2,1,4,3]

Example 2:

1
2
Input: head = []
Output: []

Example 3:

1
2
Input: head = [1]
Output: [1]

Constraints:

  • The number of nodes in the list is in the range [0, 100].

  • 0 <= Node.val <= 100

Explanation

  1. From the problem example, we need to swap 1 and 2, then swap 3 and 4. In order to swap 3 and 4, we need a pointer that can point both node. In this case, to swap 3 and 4, we need a pre-node pointing at 2, this pre-node can represent 3 using pre.next and represent 4 using pre.next.next. So, in order to swap the first two elements, we need to create a dummy node in front of the input’s head.

  2. Now, the node become this: pre->1->2->3->4. The solution basically do:

    1
    2
    3
     pre->2->3->4
 1->3->4
 pre->2->1->3->4

  3. After we swap, we move the pre pointing to pre.next.next and repeat the above process.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func swapPairs(head *ListNode) *ListNode {
    dummy := &ListNode{-1, head}
    pre := dummy
    
    for pre.Next != nil && pre.Next.Next != nil {
        cur := pre.Next
        pre.Next = cur.Next
        cur.Next = cur.Next.Next
        pre.Next.Next = cur
        
        pre = pre.Next.Next
    }
    
    return dummy.Next
}

Diagonal Traverse

Given a matrix of M x N elements (M rows, N columns), return all elements of the matrix in diagonal order as shown in the below image.

Example:

1
2
3
4
5
6
7
8
9
10
Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]

Output:  [1,2,4,7,5,3,6,8,9]

Explanation:

Diagonal Traverse

Note:

The total number of elements of the given matrix will not exceed 10,000.

Explanation

  1. We either go up right or down left directions. We also need to consider 4 different edge cases.

    1. When go up right direction, current position hit top border, we should move right (c = c + 1).
    2. When go up right direction, current position hit right border, we should move down (r = r + 1).
    3. When go down left direction, current position hit left border, we should move down (r = r + 1).
    4. When go down left direction, current position hit bottom border, we should move right (c = c + 1).

  2. If in up right direction, current position is on top right corner exactly, then we move down. If in down left direction, current position is on bottom left corner exactly, then we move right.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func findDiagonalOrder(matrix [][]int) []int {
    if len(matrix) == 0 || len(matrix[0]) == 0 { return []int{} }
    
    row, col := len(matrix), len(matrix[0])
    res := make([]int, row * col)
    r, c := 0, 0
    up := true

    for i := 0; i < row * col; i++ {
        res[i] = matrix[r][c]
        if up == true {
            if c == col - 1 {
                r += 1
                up = !up
            } else if r == 0 {
                c += 1
                up = !up
            } else {
                r -= 1
                c += 1
            }
        } else {
            if r == row - 1 {
                c += 1
                up = !up
            } else if c == 0 {
                r += 1
                up = !up
            } else {
                r += 1
                c -= 1
            }
        }
    }
    
    return res
}

Decode Ways

A message containing letters from A-Z is being encoded to numbers using the following mapping:

1
2
3
4
'A' -> 1
'B' -> 2
...
'Z' -> 26

Given a non-empty string containing only digits, determine the total number of ways to decode it.

The answer is guaranteed to fit in a 32-bit integer.

Example 1:

1
2
3
Input: s = "12"
Output: 2
Explanation: It could be decoded as "AB" (1 2) or "L" (12).

Example 2:

1
2
3
Input: s = "226"
Output: 3
Explanation: It could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).

Example 3:

1
2
3
Input: s = "0"
Output: 0
Explanation: There is no character that is mapped to a number starting with '0'. We cannot ignore a zero when we face it while decoding. So, each '0' should be part of "10" --> 'J' or "20" --> 'T'.

Example 4:

1
2
Input: s = "1"
Output: 1

Constraints:

  • 1 <= s.length <= 100

  • s contains only digits and may contain leading zero(s).

Explanation 1

  1. We can use dynamic programming to solve this problem.

  2. Dynamic state is a one dimensional array, dp[s.length()+1], and its i index element is the decode ways of the substring choosing the first i character. For example, let input string s=123, then dp[1] is the decode way of 1; dp[2] is the decode way of 12; dp[3] is the decode way of 123;

  3. Dynamic init is dp[1]=1, dp[0]=1 because later we want the dynamic function to be dp[i] = dp[i-1] + dp[i-2], so dp[2] = dp[1] + dp[0], so we need to set dp[0] to some value, dp[0] is 1 because in general case, for example string s="12", we know the decode way is 2; s="1", we know the decode way is 1, so we set dp[1]=1, so dp[0]=1.

  4. Dynamic function in general case is dp[i] = dp[i-1] + dp[i-2]. For example, s = "123", if i is iterating at character 3, then we can think of 3 as a group, 12 as another group, in this case s = "123" its decode way is the same the decode way of s=12, in other word, dp[i] = dp[i-1]. Beside this, we can think of 23 as a group, 1 as another group, in this case, its decode way is the same when s=1, in other word, dp[i] = dp[i-2].

  5. There are some special case of the above dynamic function. If the string is “120”, the current iterated element is 0, then we cannot think of 0 as a group, we need to consider “20” as a group, 1 as another group, so dp[i] = dp[i-2]. Also, if the string is “130” or “100”, then we cannot think of “0”, “30”, or “00” as a group, there is actually no way to decode such string. One more special case is when s=103, we can think of 3 as a group and 10 as another group, so dp[i]=dp[i-1], but we cannot think of 03 as group, so we cannot use dp[i]=dp[i-2].

  6. Dynamic result is dp[s.length()], which means return the decode way when we choose all the elements.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func numDecodings(s string) int {
    if s[0] == '0' { return 0 }
    
    dp := make([]int, len(s)+1)
    dp[0] = 1
    dp[1] = 1
    
    for i := 2; i <= len(s); i++ {
        if s[i-1] == '0' {
            if s[i-2] != '1' && s[i-2] != '2' {
                return 0
            }
            dp[i] = dp[i-2]
        } else {
            if s[i-2] == '0' || s[i-2: i] > "26" {
                dp[i] = dp[i-1]
            } else {
                dp[i] = dp[i-1] + dp[i-2]
            }
        }
    }
    
    return dp[len(dp)-1]
}

Explanation 2

  1. We can also use recursion to solve this problem. For example if the input string is "123". If we think of 1 as a group, then the number of decode way for 123 is the same as the number of decode way for 23.

  2. If the input string is "23". if we think of 2 as a group, then the number of decode way for 23 is the same as the number of decode way for 3.

  3. Base case is if the input string length is 1 and it’s not equal to "0", then we return 1. Since we know that "23" can have total of 2 ways to decode. One way is when we think of 2 as a group, so 3 as another group, so we return 1. Another way is when we think of 23 as a group, so an empty string "" as another group, but we still return 1. So another base case is if the input string is an empty string, we return 1.

  4. When we think of some number as a group, we need to check this number is between 1 to 26 first.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func numDecodings(s string) int {
    hm := make(map[int]int)
    return helper(s, 0, hm)
}

func helper(s string, start int, hm map[int]int) int {
    if len(s) == 1 && s[0] != '0' { return 1 }
    if start == len(s) { return 1 }
    if hm[start] > 0 { return hm[start] }
    
    cnt := 0
    for i := start; i < len(s); i++ {
        cur := s[start: i+1]
        curNum := stringToNum(cur)
        if 1 <= curNum && curNum <= 26 {
            temp := helper(s, i+1, hm)
            cnt += temp
        }
    }
    
    hm[start] = cnt
    return cnt
}

func stringToNum(s string) int {
    if s[0] == '0' { return 0 }
    num := 0
    for i := 0; i < len(s); i++ {
        num = num * 10 + int(s[i] - '0')
    }
    return num
}

Jump Game IV

Given an array of integers arr, you are initially positioned at the first index of the array.

In one step you can jump from index i to index:

  • i + 1 where: i + 1 < arr.length.

  • i - 1 where: i - 1 >= 0.

  • j where: arr[i] == arr[j] and i != j.

Return the minimum number of steps to reach the last index of the array.

Notice that you can not jump outside of the array at any time.

Example 1:

1
2
3
Input: arr = [100,-23,-23,404,100,23,23,23,3,404]
Output: 3
Explanation: You need three jumps from index 0 --> 4 --> 3 --> 9. Note that index 9 is the last index of the array.

Example 2:

1
2
3
Input: arr = [7]
Output: 0
Explanation: Start index is the last index. You don't need to jump.

Example 3:

1
2
3
Input: arr = [7,6,9,6,9,6,9,7]
Output: 1
Explanation: You can jump directly from index 0 to index 7 which is last index of the array.

Example 4:

1
2
Input: arr = [6,1,9]
Output: 2

Example 5:

1
2
Input: arr = [11,22,7,7,7,7,7,7,7,22,13]
Output: 3

Constraints:

  • 1 <= arr.length <= 5 * 10^4

  • -10^8 <= arr[i] <= 10^8

Hint 1:

Build a graph of n nodes where nodes are the indices of the array and edges for node i are nodes i+1, i-1, j where arr[i] == arr[j].

Hint 2:

Start bfs from node 0 and keep distance, answer is the distance when you reach onode n-1.

Explanation

  1. We can solve this problem using brute force with BFS. For example, if the input array is [1, 2, 7, 1, 5, 1, 8]. Start from the first number, using 1 step, we can go to [num2, secondNum1, thirdNum1]. Then, start from [num2, secondNum1, thirdNum1], using 2 step, we can go to [num7, num5, num8]. Since num8 is at the last index, we return 2.

  2. First, we need to build a graph by adjacency list. Key is the element, value is the list of indexes of this element. To prevent duplicate, we also need a visited set. Then, we can start our BFS using a queue and follow the above method to find the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
func minJumps(arr []int) int {
    if len(arr) == 1 { return 0 }
    
    graph := make(map[int][]int)
    for i := range arr {
        if _, ok := graph[arr[i]]; !ok {
            graph[arr[i]] = make([]int, 0)            
        }
        graph[arr[i]] = append(graph[arr[i]], i)
    }
    
    queue := make([]int, 0)
    visited := make(map[int]bool)
    queue = append(queue, 0)
    visited[0] = true
    cnt := 0
    
    for len(queue) > 0 {
        for i := len(queue) - 1; i >= 0; i-- {
            curIdx := queue[0]
            queue = queue[1:]
            if curIdx == len(arr)-1 { return cnt }
            
            curNum := arr[curIdx]
            for _, neighborIdx := range graph[curNum] {
                if !visited[neighborIdx] {
                    queue = append(queue, neighborIdx)
                    visited[neighborIdx] = true
                }
            }
            delete(graph, curNum)
            
            if curIdx-1 >= 0 && !visited[curIdx-1] {
                queue = append(queue, curIdx-1)
                visited[curIdx-1] = true
            }
            
            if curIdx+1 < len(arr) && !visited[curIdx+1] {
                queue = append(queue, curIdx+1)
                visited[curIdx+1] = true
            }
        }
        
        cnt += 1
    }
    
    return -1
}

Reach a Number

You are standing at position 0 on an infinite number line. There is a goal at position target.

On each move, you can either go left or right. During the n-th move (starting from 1), you take n steps.

Return the minimum number of steps required to reach the destination.

Example 1:

1
2
3
4
5
Input: target = 3
Output: 2
Explanation:
On the first move we step from 0 to 1.
On the second step we step from 1 to 3.

Example 2:

1
2
3
4
5
6
Input: target = 2
Output: 3
Explanation:
On the first move we step from 0 to 1.
On the second move we step  from 1 to -1.
On the third move we step from -1 to 2.

Note:

  • target will be a non-zero integer in the range [-10^9, 10^9].

Explanation

  1. Since the number line is symmetry, the step to reach negative target is the same as the step to reach positive target.

  2. If the target is 4, then we keep moving forward until we reach a number that is greater than or equal to target. We have:

    1
    2
    3
    4
    5
     0 + 1 = 1

 1 + 2 = 3

 3 + 3 = 6

  3. Since 6 is greater than 4, and exceed the target by 2, which is an even number. So, if when we were adding 1, instead of adding 1, we add negative 1, we will reach the target. For example:

    1
    2
    3
    4
    5
     0 - 1 = -1

 -1 + 2 = 1

 1 + 3 = 4

  4. So when we exceed the target by d, and d is an even number, when we were adding d/2, instead of adding d/2, we add -d/2, we will reach the target.

  5. If d is an odd number and the current step is n. We need to consider whether the next step n+1 is an even number or odd number. If n+1 is an odd number, then we move one more step forward, and now the d becomes even number, so we can return n+1 as our result. If n+1 is even, then n+2 will be odd, so we need to move two steps forward in order to make d even, so we return n+2 as our result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func reachNumber(target int) int {
    if target < 0 {
        target = -target
    }
    
    res, sum := 0, 0
    
    for sum < target || (sum - target) % 2 == 1 {
        res += 1
        sum += res
    }
    
    return res
}

Week 5: December 29th - December 31st

Longest Substring with At Most K Distinct Characters

Given a string s and an integer k, return the length of the longest substring of s that contains at most k distinct characters.

Example 1:

1
2
3
Input: s = "eceba", k = 2
Output: 3
Explanation: The substring is "ece" with length 3.

Example 2:

1
2
3
Input: s = "aa", k = 1
Output: 2
Explanation: The substring is "aa" with length 2.

Constraints:

  • 1 <= s.length <= 5 * 10^4

  • 0 <= k <= 50

Explanation

  1. This problem is the same as 159. Longest Substring with At Most Two Distinct Characters except we need to change k equals to 2 to any number now.

  2. First, we can create a HashMap, and use it to store the key is the character, the value is the frequency of the character. Also, we initialize the left be 0. Iterate the input string and update the hashmap. While the hashmap has size greater than k, then we need to decrease the frequency of character s[left] and increase left by 1. Also if the s[left]’s frequency is 0, we remove the key s[left] from the hashmap. Repeat these steps until the hashmap has size less than or equal to k. Next, we update the result be max(res, i-left+1).

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int lengthOfLongestSubstringKDistinct(String s, int k) {
        int res = 0;
        Map<Character, Integer> hm = new HashMap<>();
        int left = 0;

        for (int i = 0; i < s.length(); i++) {
            char cur = s.charAt(i);
            hm.put(cur, hm.getOrDefault(cur, 0) + 1);
            
            while (hm.size() > k) {
                char leftChar = s.charAt(left);
                hm.put(leftChar, hm.get(leftChar) - 1);
                if (hm.get(leftChar) == 0) hm.remove(leftChar);
                left += 1;
            }
            
            res = Math.max(res, i - left + 1);
        }
        
        return res;
    }
}

Pseudo-Palindromic Paths in a Binary Tree

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

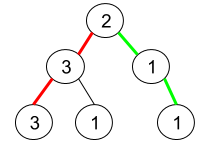
Pseudo-Palindromic Paths in a Binary Tree

1
2
3
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

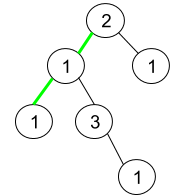
Pseudo-Palindromic Paths in a Binary Tree

1
2
3
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

1
2
Input: root = [9]
Output: 1

Constraints:

  • The given binary tree will have between 1 and 10^5 nodes.

  • Node values are digits from 1 to 9.

Hint 1:

Note that the node values of a path form a palindrome if at most one digit has an odd frequency (parity).

Hint 2:

Use a Depth First Search (DFS) keeping the frequency (parity) of the digits. Once you are in a leaf node check if at most one digit has an odd frequency (parity).

Explanation

  1. We can use brute force to solve this problem. First, build all the root-to-leaf paths. Then count every path that is palindrome and return the counter as the result.

  2. We can use pre-order traversal to iterate every element and save each root-to-leaf path into each list, but this is space consuming. To save space, we can use an integer to hold the path by using bitwise operation. The idea is to keep the frequency of digit 1 in the first bit, 2 in the second bit, etc: path ^= (1 << node.val). For example, the first time when we iterate the node value 2, we have path = 010; the second time when we iterate the node value 2, we have path = 000; the third time when we iterate the node value 2, we have path = 010.

  3. If the root-to-leaf path is palindrome, then at most one digit has an odd frequency. To determine if path is palindrome, we can turn off (= setting to 0) the rightmost 1-bit by path & (path - 1) then check if path become 0. If path becomes 0, then we find a palindrome path and increase our counter.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func pseudoPalindromicPaths (root *TreeNode) int {
    res, path := 0, 0
    helper(root, path, &res)
    return res
}

func helper(root *TreeNode, path int, res *int) {
    if root == nil { return }
    path = path ^ (1 << root.Val)
    if root.Left == nil && root.Right == nil {
        if (path & (path - 1)) == 0 {
            *res += 1
        }
    }
    helper(root.Left, path, res)
    helper(root.Right, path, res)
}

Game of Life

According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.”

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

  1. Any live cell with fewer than two live neighbors dies as if caused by under-population.

  2. Any live cell with two or three live neighbors lives on to the next generation.

  3. Any live cell with more than three live neighbors dies, as if by over-population.

  4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.

Example 1:

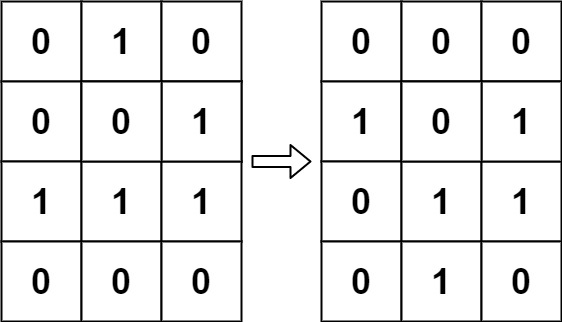
Game of Life

1
2
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

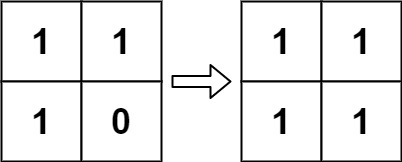
Game of Life

1
2
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

  • m == board.length

  • n == board[i].length

  • 1 <= m, n <= 25

  • board[i][j] is 0 or 1.

Follow up:

  • Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.

  • In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

Explanation

  1. First, we define the 4 states, and update all cells to the state.
    1. State 0: die cell to die cell
    2. State 1: live cell to live cell
    3. State 2: live cell to die cell
    4. State 3: die cell to live cell

  2. After we update every cell to its state, we can loop through all the cell again and update to the final result of the each cell. We can use their state number module 2 to get the final result. In other words, if the module result is 0 (state0 and state2), final result will be 0. Else if the module result is not 0 (state 1 and state 3), final result will be 1.

  3. We need a counter live to count how many live neighbor in each cell’s 8 neighbors. If the neighbor cell value is 1 or 2, that means they are live cell originally. After scanning every cell’s 8 neighbors, if the live counter is less than 2 or greater than 3, and the current cell is live cell, then mark the current cell to state 2. If there are exactly 3 live counter, and the current cell is die cell, then mark it as state 3.

  4. After we update every cell’s state, we loop through the board again, and for each cell, we module 2 to get each cell’s final result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func gameOfLife(board [][]int)  {
    row, col := len(board), len(board[0])
    dx := []int{-1, -1, -1, 0, 0, 1, 1, 1}
    dy := []int{-1, 0, 1, -1, 1, -1, 0, 1}
    
    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            live := 0

            for i := 0; i < 8; i++ {
                x, y := r+dx[i], c+dy[i]
                    if x >= 0 && x < row && y >= 0 && y < col && (board[x][y]==1 || board[x][y]==2) {
                        live += 1;
                    }
            }
            
            if board[r][c] != 0 && (live < 2 || live > 3) {
                board[r][c] = 2
            } else if board[r][c] == 0 && live == 3 {
                board[r][c] = 3
            }
        }
    }
    
    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            board[r][c] %= 2
        }
    }
}

Largest Rectangle in Histogram

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

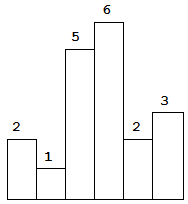
Largest Rectangle in Histogram

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

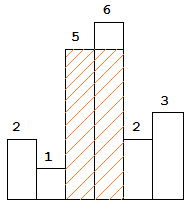
Largest Rectangle in Histogram

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

1
2
Input: [2,1,5,6,2,3]
Output: 10

Explanation 1

  1. Iterate each element, if the next element is less than the current element or we hit the end of the array, then we start to find the rectangle’s area and that rectangle’s right side is fixed on current index.

  2. We can find the min height by loop backward from the current index to zero, and we multiple the width with the minHeight.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func largestRectangleArea(heights []int) int {
    if len(heights) < 1 { return 0 }
    res := 0
    
    for cur := 0; cur < len(heights); cur++ {
        if cur == len(heights) - 1 || heights[cur+1] < heights[cur] {
            minHeight := heights[cur]
            for j := cur; j >= 0; j-- {
                width := cur - j + 1
                if heights[j] < minHeight { minHeight = heights[j] }
                res = max(res, width * minHeight)
            }
        }
    }
    
    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Explanation 2

  1. We can find the area by finding the current element’s leftMost and rightMost index and area = heights[cur] * (rightMost-leftMost-1). From the above example, if the current element is at index 2, its height is 5. Then the leftMost is at index 1, and rightMost is at index 4 (leftMost is the previous first index element height that is less than the current element height, rightMost is the next first index element height that is less than the current element height). So, when current index is 2, its maximum area is 5 * (4-1-1) = 10 which shows the red area. Another example is when current index is 3 which is at height 6, its maximum area is 6 * (4-2-1) = 6.

  2. First, we create an array leftMost[] to store every corresponding element’s leftMost index, similarlly create another array rightMost[] to store every corresponding element’s rightMost index.

  3. When we are iterating the original array and find the leftMost index for the current element at index i, in other words, to find leftMost[i]. We first think of the leftMost index l is i-1. While heights[l] is greater than or equal to heights[i], we decreasing l. Outside this while loop, l will be the first index of the element height less than the current height heights[i], so leftMost[i] = l. When we are decreasing l this takes O(n) time, instead, we can improve the time complexity by setting l = leftMost[l]. Similarlly, for rightMost index r, we set r = rightMost[r].

  4. After we calculate the results for leftMost[] and rightMost[], we can iterate the input array one more time and use step 1’s formula (area = heights[cur] * (rightMost[cur]-leftMost[cur]-1)) to calculate the maximum area.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func largestRectangleArea(heights []int) int {
    if len(heights) < 1 { return 0 }
    res := 0
    leftMost := make([]int, len(heights))
    rightMost := make([]int, len(heights))
    leftMost[0] = -1;
    rightMost[len(heights)-1] = len(heights)
    
    for i := 1; i < len(heights); i++ {
        l := i - 1
        for l >= 0 && heights[l] >= heights[i] {
            l = leftMost[l]
        }
        leftMost[i] = l
    }
    
    for i := len(heights) - 2; i >= 0; i-- {
        r := i + 1
        for r < len(heights) && heights[r] >= heights[i] {
            r = rightMost[r]
        }
        rightMost[i] = r
    }
    
    for i := 0; i < len(heights); i++ {
        curArea := heights[i] * (rightMost[i] - leftMost[i] - 1)
        if res < curArea {
            res = curArea
        }
    }
    
    return res
}