Happy 2021! It’s been a long year working from home. In 2020, I used Go for leetcoding, read some JavaScript books, and watched tutorials about JavaScript, Node.js, DOM, and CSS. This year I will improve my JavaScript data structure, indepth of Node.js, front-end, and back-end development, and learn some Web Assembly.
Week 1: January 1st - January 7th
Palindrome Permutation
Given a string, determine if a permutation of the string could form a palindrome.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Hint 1:
Consider the palindromes of odd vs even length. What difference do you notice?
Hint 2:
Count the frequency of each character.
Hint 3:
If each character occurs even number of times, then it must be a palindrome. How about character which occurs odd number of times?
Explanation
-
A even length palindrome means every number appears even number of times. An odd length palindrome means there’s only one number appear odd number of times.
-
We can first count every number’s frequency, then we loop through the hashmap and count how many odd number frequency. If ther are more than one odd number frequency then we can return false immediately. At the end, we return true.
Solution
1 | |
Check Array Formation Through Concatenation
You are given an array of distinct integers arr and an array of integer arrays pieces, where the integers in pieces are distinct. Your goal is to form arr by concatenating the arrays in pieces in any order. However, you are not allowed to reorder the integers in each array pieces[i].
Return true if it is possible to form the array arr from pieces. Otherwise, return false.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Example 5:
1 | |
Constraints:
-
1 <= pieces.length <= arr.length <= 100 -
sum(pieces[i].length) == arr.length -
1 <= pieces[i].length <= arr.length -
1 <= arr[i], pieces[i][j] <= 100 -
The integers in
arrare distinct. -
The integers in
piecesare distinct (i.e., If we flatten pieces in a 1D array, all the integers in this array are distinct).
Hint 1:
Note that the distinct part means that every position in the array belongs to only one piece
Hint 2:
Note that you can get the piece every position belongs to naively
Explanation
-
Loop through the
pieces[]array, for everypieces[i], we store its first elementpieces[i][0]and the pieces indexiinto a hashmap as key value pair. -
Next, we loop through the array
arr, if the current elementarr[i]is not in the hashmap, that means its not the first piece element so we return false. Else, we can get the piece indexpIdx = hm.get(arr[i]), and start comparingarr[i]withpieces[PIdx][j]wherejis the index for the subarraypieces[Pidx].
Solution
1 | |
Find a Corresponding Node of a Binary Tree in a Clone of That Tree
Given two binary trees original and cloned and given a reference to a node target in the original tree.
The cloned tree is a copy of the original tree.
Return a reference to the same node in the cloned tree.
Note that you are not allowed to change any of the two trees or the target node and the answer must be a reference to a node in the cloned tree.
Follow up: Solve the problem if repeated values on the tree are allowed.
Example 1:
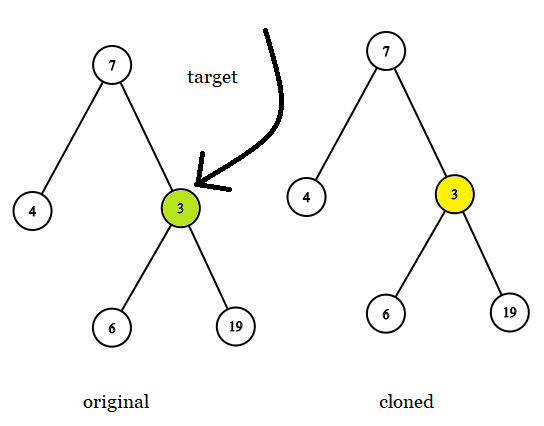
1 | |
Example 2:
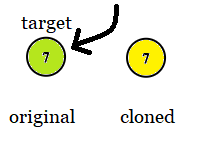
1 | |
Example 3:
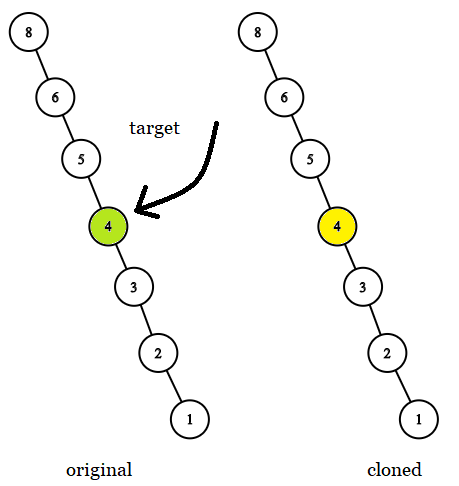
1 | |
Example 4:
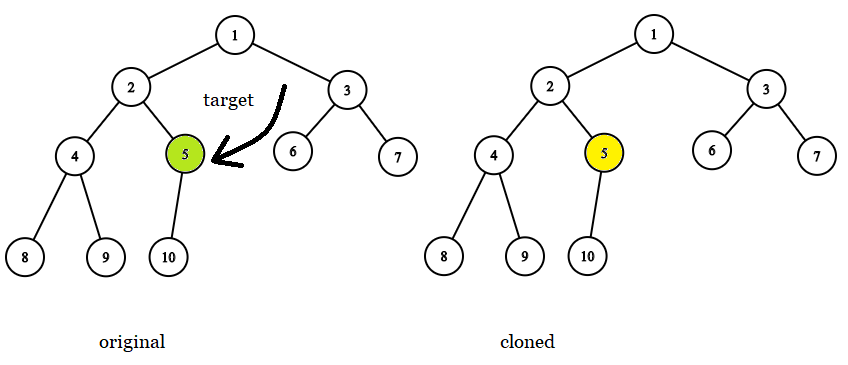
1 | |
Example 5:
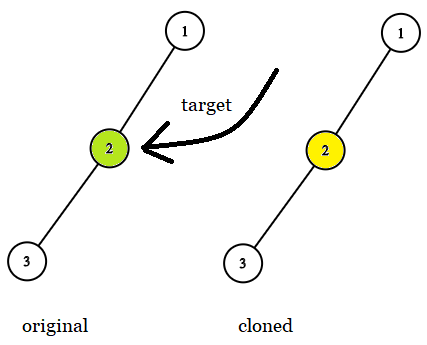
1 | |
Constraints:
-
The number of nodes in the
treeis in the range[1, 10^4]. -
The values of the nodes of the
treeare unique. -
targetnode is a node from theoriginaltree and is notnull.
Explanation
- This is a tree traversal probelm. We can traversal the tree, when we find an target node equal to the original node, then we can return the corresponding cloned node.
Solution
1 | |
Beautiful Arrangement
Suppose you have n integers labeled 1 through n. A permutation of those n integers perm (1-indexed) is considered a beautiful arrangement if for every i (1 <= i <= n), either of the following is true:
-
perm[i]is divisible byi. -
iis divisible byperm[i].
Given an integer n, return the number of the beautiful arrangements that you can construct.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
1 <= n <= 15
Explanation
- We can use DFS recursion to solve this problem. We need a visited array to record whether the number is visited or not in the result permutation. We initialize the result permutation position
posto 1. In the recursive helper function, the base case is ifpos == N+1, then it means we finish iterating all the numbers from 1 toN, so we increaseres. The recursion function will be a for loopifrom 1 toNinclusive. If the current numberiis not visited andi % pos == 0orpos % i == 0, then we markivisited and recursivly call the helper function withpos + 1. After the helper function, we need to backtract thevisited[i] = false.
Solution
1 | |
Merge Two Sorted Lists
Merge two sorted linked lists and return it as a sorted list. The list should be made by splicing together the nodes of the first two lists.
Example 1:
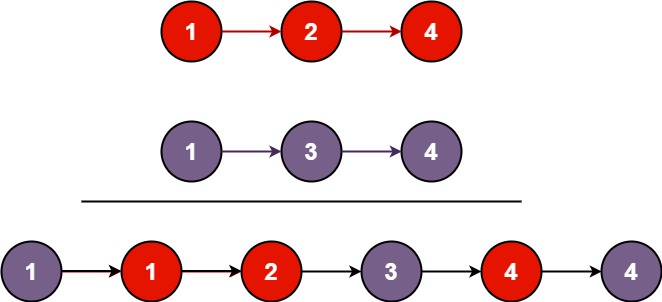
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
The number of nodes in both lists is in the range
[0, 50]. -
-100 <= Node.val <= 100 -
Both
l1andl2are sorted in non-decreasing order.
Explanation 1
-
First, create a ListNode to hold the result.
-
While
l1andl2are not null, comparel1andl2’s value and putting the smaller one to the result ListNode. -
We need a pointer pointing to the result node.
Solution 1
1 | |
Explanation 2
- We can compare the
l1andl2’s first node value, ifl1’s node value is smaller, then recusivly comparel1.nextwithl2, vice versa. If one of the ListNode is null, simply return another ListNode.
Solution 2
1 | |
Remove Duplicates from Sorted List II
Given the head of a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list. Return the linked list sorted as well.
Example 1:
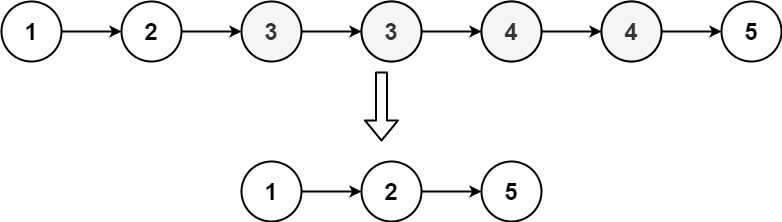
1 | |
Example 2:
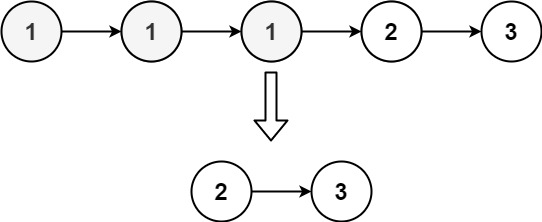
1 | |
Constraints:
-
The number of nodes in the list is in the range
[0, 300]. -
-100 <= Node.val <= 100
The list is guaranteed to be sorted in ascending order.
Explanation
-
We need to check if the current element is same as its previous element and its next element, so we need to create a dummy node, and a pre pointer initially points at the dummy node, a current pointer initially points at the first element, and we compare current pointer element with pre pointer element and current.next element.
-
If the current element is not the same as its previous and next element, then we need to store it into a linkedlist, so we can store the first distinct element into
dummy.next, at the end we can returndummy.next. -
After we store the matching current element, we need to move
preandcurpointers to point at the next element. Because nowcurpoints at the correct next element and we want to cut off the result list and input list, we can setpre.nexttonull, one example is input list is[1, 2, 2], we want the result list to be[1]. Also, initially, thedummy.nextisnulland it’s not pointing to the head of the input linkedlist.
Solution
1 | |
Kth Missing Positive Number
Given an array arr of positive integers sorted in a strictly increasing order, and an integer k.
Find the kth positive integer that is missing from this array.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
1 <= arr.length <= 1000 -
1 <= arr[i] <= 1000 -
1 <= k <= 1000 -
arr[i] < arr[j]for1 <= i < j <= arr.length
Hint 1:
Keep track of how many positive numbers are missing as you scan the array.
Explanation 1
- We can use brute force to solve this problem. First, create a variable
counterand a variablemissingto count number of missing. Then, loop through the array, comparecounterwith the current iterated number. Whilecounteris less thannum, then we increasemissing. Ifmissingreachesk, we returncounter, else, we increasecounter. After finish looping all numbers, ifmissingis less thank, then we returnarr[arr.length-1] + (k - missing).
Solution 1
1 | |
Explanation 2
-
We are maintaining such invariant throughout the loop:
left + k <= res <= right + k. Obviously when the array is missingkor more elements in the beginning,res = k; when there is no missing elements, ans isarr.length + k. -
The number of missing is equals to
A[m] - m - 1wheremis the number of not missing. -
We can use binary search to find the first element at index
leftto make the number of missing equals tok. -
left + kis the kth missing number because in the range of[1, left+k], there areleftnumbers not missing, andknumbers are missing.
Solution 2
1 | |
Longest Substring Without Repeating Characters
Given a string s, find the length of the longest substring without repeating characters.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Constraints:
-
0 <= s.length <= 5 * 10^4 -
sconsists of English letters, digits, symbols and spaces.
Explanation
-
We can solve this problem using sliding window technique. Think of we will maintain a window that contains all unique characters. First initialize
windowStartandwindowEndto 0. Also, initialize a hashset to record the window’s unique characters. -
Loop the
windowEndfrom index 0 to the last index of the input string. While the set contains the current iterated character, we remove the window’s left characterstr[windowStart]and movewindowStart1 step forward, repeat this while loop until the set doesn’t contains the incoming iterated character. Next, we add the iterated character into the set, then calculate the result bemax(res, windowEnd - windowStart + 1).
Solution
1 | |
Week 2: January 8th - January 14th
Find Root of N-Ary Tree
You are given all the nodes of an N-ary tree as an array of Node objects, where each node has a unique value.
Return the root of the N-ary tree.
Custom testing:
An N-ary tree can be serialized as represented in its level order traversal where each group of children is separated by the null value (see examples).
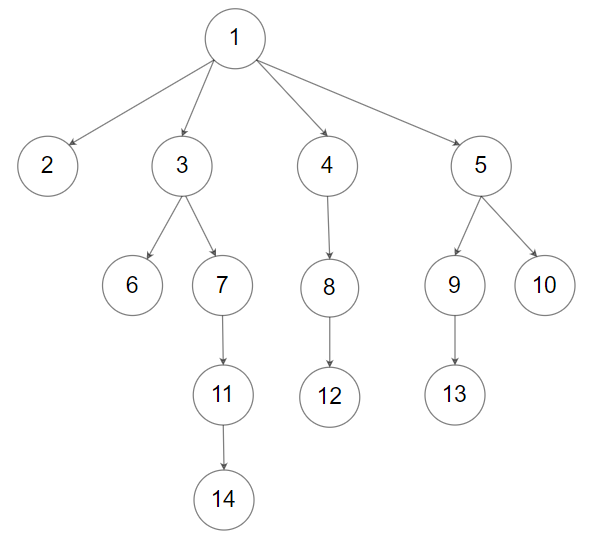
For example, the above tree is serialized as
[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14].
The testing will be done in the following way:
-
The input data should be provided as a serialization of the tree.
-
The driver code will construct the tree from the serialized input data and put each
Nodeobject into an array in an arbitrary order. -
The driver code will pass the array to
findRoot, and your function should find and return the rootNodeobject in the array. -
The driver code will take the returned
Nodeobject and serialize it. If the serialized value and the input data are the same, the test passes.
Example 1:
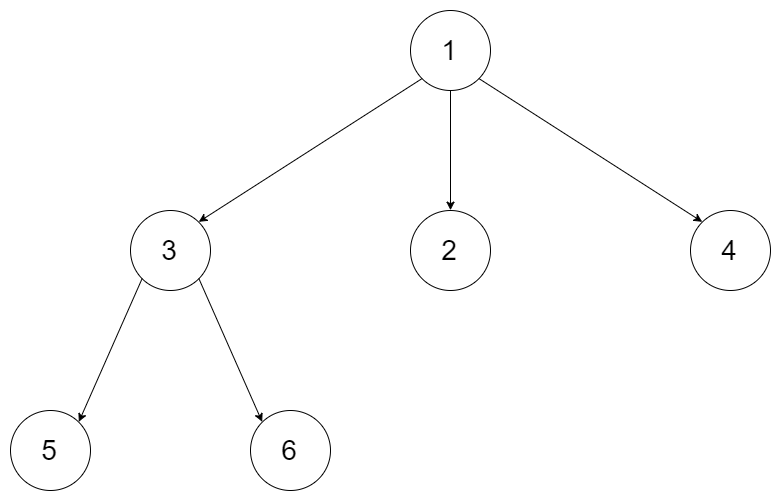
1 | |
Example 2:
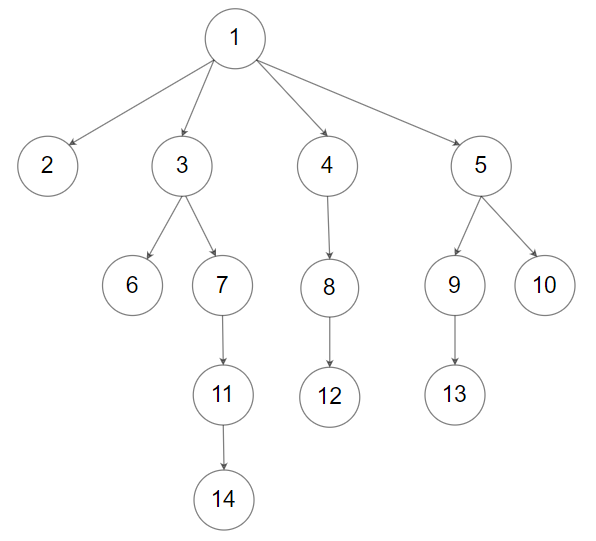
1 | |
Constraints:
-
The total number of nodes is between
[1, 5 * 10^4]. -
Each node has a unique value.
Follow up:
- Could you solve this problem in constant space complexity with a linear time algorithm?
Hint 1:
Node with indegree 0 is the root
Explanation 1
- Loop through all the nodes, in each iteration, we add the current node’s children nodes into a visited set. At the end, only the root node would not be in the set.
Solution 1
1 | |
Explanation 2
- Instead of using a set, we can create a variable
sum. We increase the current iterated node’s value, subtract its children node’s values. At the end, thesumis equal to the root node’s value since all nodes are unique.
Solution 2
1 | |
Explanation 3
- Instead of summing and subtracting, we can do XOR.
Solution 3
1 | |
Check If Two String Arrays are Equivalent
Given two string arrays word1 and word2, return true if the two arrays represent the same string, and false otherwise.
A string is represented by an array if the array elements concatenated in order forms the string.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
1 <= word1.length, word2.length <= 10^3 -
1 <= word1[i].length, word2[i].length <= 10^3 -
1 <= sum(word1[i].length), sum(word2[i].length) <= 10^3 -
word1[i]andword2[i]consist of lowercase letters.
Hint 1:
Concatenate all strings in the first array into a single string in the given order, the same for the second array.
Hint 2:
Both arrays represent the same string if and only if the generated strings are the same.
Explanation
- Brute force approach will be concatenate all words in the array and compare two strings to see if they are equal. It will takes too many space if there are many words in the array. A better approach is creating two pointers for each array:
wordIdxfor iterating the array andstrIdxto iterate character inside each word. Then we compare character by character to see if it’s equal.
Solution
1 | |
Word Ladder
Given two words beginWord and endWord, and a dictionary wordList, return the length of the shortest transformation sequence from beginWord to endWord, such that:
-
Only one letter can be changed at a time.
-
Each transformed word must exist in the word list.
Return 0 if there is no such transformation sequence.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
1 <= beginWord.length <= 100 -
endWord.length == beginWord.length -
1 <= wordList.length <= 5000 -
wordList[i].length == beginWord.length -
beginWord,endWord, andwordList[i]consist of lowercase English letters. -
beginWord != endWord -
All the strings in
wordListare unique.
Explanation
-
We can try brute force. For every character in the word, we try to replace each character with ‘a’ to ‘z’. For example, “hit”, we replace the first character with “a”, so it is “ait”; replace it with “b”, so it is “bit”; and we get “cit”, “dit”, “eit”, …, “zit”. We check if these words if it’s the endWord, if not, check if they are in the list, if the word is in the list, then it can potentially be the path to get the endWord.
-
Now, if the word we try is “hot”, and we check it’s in the list, then should we try “hpt”, “hqt”, “hrt”… (BFS) or “aot”, “bot”, “cot”… (DFS)? We know that it’s better to use BFS to find the minimum path, so it’s better to use BFS. After we find a word that is equal to the endWord, we can return the level plus one immediately, we plus one because the beginWord count once.
Solution
1 | |
Create Sorted Array through Instructions
Given an integer array instructions, you are asked to create a sorted array from the elements in instructions. You start with an empty container nums. For each element from left to right in instructions, insert it into nums. The cost of each insertion is the minimum of the following:
-
The number of elements currently in
numsthat are strictly less thaninstructions[i]. -
The number of elements currently in
numsthat are strictly greater thaninstructions[i].
For example, if inserting element 3 into nums = [1,2,3,5], the cost of insertion is min(2, 1) (elements 1 and 2 are less than 3, element 5 is greater than 3) and nums will become [1,2,3,3,5].
Return the total cost to insert all elements from instructions into nums. Since the answer may be large, return it modulo 10^9 + 7
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
1 <= instructions.length <= 10^5 -
1 <= instructions[i] <= 10^5
Hint 1:
This problem is closely related to finding the number of inversions in an array
Hint 2:
if i know the position in which i will insert the i-th element in I can find the minimum cost to insert it
Explanation
-
This is a Binary Indexed Tree (Fenwick Tree) problem. We store the frequency of the element into the fenwick tree, at the same time, we can calculate the left cost and right cost. If the current element is
n, then the left costleftis the total frequency from 1 ton-1inclusive; the right costrightis the total number of element in the tree, in other word, the current indexi, subtract the total frequency from 1 toninclusive. -
Let
Nbe the length of instructions andMbe the maximum value in instructions.-
Time Complexity: $O(Nlog(M))$. We need to iterate over instructions, and for each element, the time to find the left cost and right cost is $O(log(M))$, and we spend $O(log(M))$ inserting the current element into the BIT. In total, we need $O(N⋅log(M))=O(Nlog(M))$.
-
Space Complexity: $O(M)$, since we need an array of size $O(M)$ to store BIT.
-
Source: https://leetcode.com/problems/create-sorted-array-through-instructions/solution/
Solution
1 | |
Merge Sorted Array
Given two sorted integer arrays nums1 and nums2, merge nums2 into nums1 as one sorted array.
The number of elements initialized in nums1 and nums2 are m and n respectively. You may assume that nums1 has enough space (size that is equal to m + n) to hold additional elements from nums2.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
0 <= n, m <= 200 -
1 <= n + m <= 200 -
nums1.length == m + n -
nums2.length == n -
-10^9 <= nums1[i], nums2[i] <= 10^9
Hint 1:
You can easily solve this problem if you simply think about two elements at a time rather than two arrays. We know that each of the individual arrays is sorted. What we don’t know is how they will intertwine. Can we take a local decision and arrive at an optimal solution?
Hint 2:
If you simply consider one element each at a time from the two arrays and make a decision and proceed accordingly, you will arrive at the optimal solution.
Explanation
-
First, getting the correct end index of the merged array, then we can try to compare the end element of both array and putting the bigger one to the end index of the result array.
-
If one array is finish putting all elements to the result array, then we can simply copy all the elements of another array to the result array.
Solution
1 | |
Add Two Numbers
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
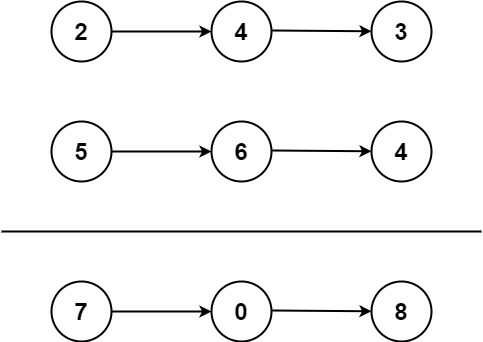
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
The number of nodes in each linked list is in the range
[1, 100]. -
0 <= Node.val <= 9 -
It is guaranteed that the list represents a number that does not have leading zeros.
Explanation
-
Create a dummy node and a pointer
curpointing to it. Whilel1orl2is notNULL, getl1’s value andl2’s value, sum them up plus carry, module 10 to be thecurnode’s next node value, then update the pointercurto be its next node, and updatel1andl2to be their next node. -
Outside of the while loop, when both
l1andl2are null, if the carry is not zero, we create a node of the carry’s value and append to the result ListNode.
Solution
1 | |
Boats to Save People
The i-th person has weight people[i], and each boat can carry a maximum weight of limit.
Each boat carries at most 2 people at the same time, provided the sum of the weight of those people is at most limit.
Return the minimum number of boats to carry every given person. (It is guaranteed each person can be carried by a boat.)
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Note:
-
1 <= people.length <= 50000 -
1 <= people[i] <= limit <= 30000
Explanation
- Since the boat can carray at most 2 people at the same time, we can pair the lightest person with the heaviest person. If these two people’s weight exceed the limit, we let the heaviest person take the boat. Else we pair the next lightest person with the next heaviest person.
Solution
1 | |
Minimum Operations to Reduce X to Zero
You are given an integer array nums and an integer x. In one operation, you can either remove the leftmost or the rightmost element from the array nums and subtract its value from x. Note that this modifies the array for future operations.
Return the minimum number of operations to reduce x to exactly 0 if it’s possible, otherwise, return -1.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
1 <= nums.length <= 10^5 -
1 <= nums[i] <= 10^4 -
1 <= x <= 10^9
Hint 1:
Think in reverse; instead of finding the minimum prefix + suffix, find the maximum subarray.
Hint 2:
Finding the maximum subarray is standard and can be done greedily.
Explanation 1
-
This problem can be transformed to 325. Maximum Size Subarray Sum Equals k.
-
In 325. Maximum Size Subarray Sum Equals k, we loop through the array, put the accumulate sum into a hashmap as key, index as value. Before we put into the hashmap, we check the
target = sum - kiftargetis inside the map, we can update the size of the subarray equalskin other words,res = max(res, i - hm[target]).
Solution 1
1 | |
Explanation 2
- We can also use two pointers to solve this problem. First, count the total sum of the array and make a variable
cur = totalSum. Looprightfrom first index to last index, each iteration, we subtractcurfromnums[right]to getcur. Whilecuris less thank, we increasecurwithnums[left]then moveleft1 step forward. Whencur == kwe update the result. The length will be from the first element toleftexclusive, and fromright+1to the last element.
Solution 2
1 | |
Week 3: January 15th - January 21st
Nested List Weight Sum
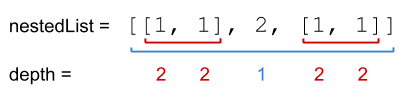
You are given a nested list of integers nestedList. Each element is either an integer or a list whose elements may also be integers or other lists.
The depth of an integer is the number of lists that it is inside of. For example, the nested list [1,[2,2],[[3],2],1] has each integer’s value set to its depth.
Return the sum of each integer in nestedList multiplied by its depth.
Example 1:
1 | |
Example 2:

1 | |
Example 3:
1 | |
Constraints:
-
1 <= nestedList.length <= 50 -
The values of the integers in the nested list is in the range
[-100, 100]. -
The maximum depth of any integer is less than or equal to
50.
Explanation 1
-
We can use recursion or DFS to solve this problem. The recursive helper function will have 2 arguments. One is the input list, another one is the current depth.
-
Inside the helper function, we loop through the input list. If the current element is an integer, we can update the result. Else if it’s a list, then we can recursively call the helper function pass this current list and increase the depth.
Solution 1
1 | |
Explanation 2
- We can also use BFS to solve this problem. First, put all the elements from the input list into the queue. Initialize the current depth is 1. Loop through the current level (current depth) from the queue, if the current element is an integer, we update the result. Else if it’s a list, then we append the list’s elements into the queue. When we finish iterating the current level, we increase the depth.
Solution 2:
1 | |
Get Maximum in Generated Array
You are given an integer n. An array nums of length n + 1 is generated in the following way:
-
nums[0] = 0 -
nums[1] = 1 -
nums[2 * i] = nums[i]when2 <= 2 * i <= n -
nums[2 * i + 1] = nums[i] + nums[i + 1]when2 <= 2 * i + 1 <= n
Return the maximum integer in the array nums.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
0 <= n <= 100
Hint 1:
Try generating the array.
Hint 2:
Make sure not to fall in the base case of 0.
Explanation
-
We can generate the array and find the maximum element on the fly.
-
From example 1, we know that if
iis even number, thenarr[i] = arr[i / 2]. Else ifiis odd number, thenarr[i] = arr[i / 2] + arr[i / 2 + 1].
Solution
1 | |
Kth Largest Element in an Array
Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.
Example 1:
1 | |
Example 2:
1 | |
Note:
You may assume k is always valid, 1 ≤ k ≤ array’s length.
Explanation
-
We can use quick sort’s partition function to solve this problem in $O(N)$ time complexity because partition function return us the correct index, where all elements on the left side of the index are greather than this index number, all elements are on the right side of this index number are less than this index number. Note, we are sorting from largest to smallest.
-
First, we make a left pointer and right pointer that point to index 0 and the right most index. If the partition function return us
pwhich equals tok-1, then we returnnums[k-1]. Else ifk-1is greather thanp, then left pointer moves top+1, else ifk-1is smaller thanp, then right pointer moves top-1. -
Inside the partition function, we first mark the first element as pivot. Left pointer moves one step forward, which is
left+1, right poitner is the last index. While left pointer is smaller or equal to the right pointer, we start a while loop. If the left pointer number is smaller than the value of pivot and right pointer value is greather than pivot value, swap the left pointer and right pointer value. Then, if the left pointer value is greater or equal to the pivot value, then left pointer move right one step. If the right pointer value is smaller or equal than pivot, then right pointer value move left one step. -
Out of the while loop, we swap pivot and the right pointer. Now, pivot is at its correct index. We finally return its index, which is the right pointer.
Solution
1 | |
Count Sorted Vowel Strings
Given an integer n, return the number of strings of length n that consist only of vowels (a, e, i, o, u) and are lexicographically sorted.
A string s is lexicographically sorted if for all valid i, s[i] is the same as or comes before s[i+1] in the alphabet.
Example 1:
1 | |
Explanation 2:
1 | |
Explanation 3:
1 | |
Constraints:
1 <= n <= 50
Hint 1:
For each character, its possible values will depend on the value of its previous character, because it needs to be not smaller than it.
Hint 2:
Think backtracking. Build a recursive function count(n, last_character) that counts the number of valid strings of length n and whose first characters are not less than last_character.
Hint 3:
In this recursive function, iterate on the possible characters for the first character, which will be all the vowels not less than last_character, and for each possible value c, increase the answer by count(n-1, c).
Explanation
- If we know all the string of len k, so the string of len k + 1 will be
- add a before all string of len k
- add e before the string of len k, which is starts with or after e
- add i before the string of len k, which starts with or after i
- add o before the string of len k, which starts with or after o
- add u before the string of len k, which starts with or after u
Source: Java DP O(n) time Easy to understand
Solution
1 | |
Max Number of K-Sum Pairs
You are given an integer array nums and an integer k.
In one operation, you can pick two numbers from the array whose sum equals k and remove them from the array.
Return the maximum number of operations you can perform on the array.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
1 <= nums.length <= 10^5 -
1 <= nums[i] <= 10^9 -
1 <= k <= 10^9
Hint 1:
The abstract problem asks to count the number of disjoint pairs with a given sum k.
Hint 2:
For each possible value x, it can be paired up with k - x.
Hint 3:
The number of such pairs equals to min(count(x), count(k-x)), unless that x = k / 2, where the number of such pairs will be floor(count(x) / 2).
Explanation 1
- We can use two pointers to solve this problem. First, sort the array. Then we make one ponter
iin the first index, another pointerjin the last index. If these two pointing numbers’ sum is equal tok, then we update the result, increaseiand decreasej. Else if sum is smaller, then we increaseionly. Else we decreasejonly.
Solution 1
1 | |
Explanation 2
-
The maximum number of pair will be
len(array) / 2. -
Create a hashmap to record the frequency of the numbers. Iterate the map, if the current element is different from the target
k - curNum, then the max pair will be the minimum between the current number’s frequency and the target’s frequency. Later will will divide this result by 2. For example[2, 3], k = 5,2’s target is3and3’s target is2. Else if current number and target are equal, then the pair will be current number’s frequency divide by 2. For example[3, 3, 3], k = 6, there is only one pair.
Solution 2
1 | |
Longest Palindromic Substring
Given a string s, return the longest palindromic substring in s.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Constraints:
-
1 <= s.length <= 1000 -
sconsist of only digits and English letters (lower-case and/or upper-case),
Hint 1:
How can we reuse a previously computed palindrome to compute a larger palindrome?
Hint 2:
If “aba” is a palindrome, is “xabax” a palindrome? Similarly is “xabay” a palindrome?
Hint 3:
Complexity based hint: If we use brute-force and check whether for every start and end position a substring is a palindrome we have O(n^2) start - end pairs and O(n) palindromic checks. Can we reduce the time for palindromic checks to O(1) by reusing some previous computation.
Explanation
-
If input string has length less than 2, simply return the string.
-
To find palindromic string, we can loop through the input string character and each character we make it as the middle of the palindromic.
-
Palindrom has 2 situations: First situation,
abcba, here,cis the middle; Second situation,abba, here,bbis the middle. -
In each iteration, we make the current character as the middle. We need to check if the current character is the same as its next character, if not the same, then we consider first situation; else, we consider the second situation.
-
We can define
leftandrightpointing the middle characters. In the fist situation,leftandrightarec. In the second situation,leftis firstb,rightis secondb. -
Then, we compare the middle’s left character and middle’s right character, in other words,
str[left-1]comparing tostr[right+1]. While they are the same,left = left-1andright=right+1. After the while loop,leftis pointing at the palindrome’s beginning index, andrightis pointing at the palindrome’s last index.right-left+1is its length. At the end of each iteration, we update the maximum length. -
After we finish the loop using the last index of the string as middle, we can return the longest pralindrome substring using the
leftand its maximum length.
Solution
1 | |
Valid Parentheses
Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
-
Open brackets must be closed by the same type of brackets.
-
Open brackets must be closed in the correct order.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Example 5:
1 | |
Constraints:
-
1 <= s.length <= 10^4 -
sconsists of parentheses only'()[]{}'.
Hint 1:
An interesting property about a valid parenthesis expression is that a sub-expression of a valid expression should also be a valid expression. (Not every sub-expression) e.g.
1 | |
Can we exploit this recursive structure somehow?
Hint 2:
What if whenever we encounter a matching pair of parenthesis in the expression, we simply remove it from the expression? This would keep on shortening the expression. e.g.
1 | |
Hint 3:
The stack data structure can come in handy here in representing this recursive structure of the problem. We can’t really process this from the inside out because we don’t have an idea about the overall structure. But, the stack can help us process this recursively i.e. from outside to inwards.
Explanation
-
Using stack.
-
Iterate the input string, if the current character is open symbol, we put its corresponding closed symbol to the stack. If the character is closed symbol, we compare the pop element of the stack with the current character. If they are not equal, we return
false, or if the stack is empty, we returnfalse. At the end If the stack is empty, we returntrue, otherwise, we returnfalse.
Solution
1 | |
Find the Most Competitive Subsequence
Given an integer array nums and a positive integer k, return the most competitive subsequence of nums of size k.
An array’s subsequence is a resulting sequence obtained by erasing some (possibly zero) elements from the array.
We define that a subsequence a is more competitive than a subsequence b (of the same length) if in the first position where a and b differ, subsequence a has a number less than the corresponding number in b. For example, [1,3,4] is more competitive than [1,3,5] because the first position they differ is at the final number, and 4 is less than 5.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
1 <= nums.length <= 10^5 -
0 <= nums[i] <= 10^9 -
1 <= k <= nums.length
Hint 1:
In lexicographical order, the elements to the left have higher priority than those that come after. Can you think of a strategy that incrementally builds the answer from left to right?
Explanation
-
We can solve this problem using monotonic stack.
-
When we iterate to
nums[i], Whilenums[i]is less than the top element of the stack, then we need to pop the stack. In this problem, we also need to maintain a size ofk, so before we pop, we check the size of the stack after we pop isstack.length - 1, and there arenums.length - ielements we can push, so these two numbers’ sum at least bekthen we can pop. Next, if stack size is less thank, we can push the current element. -
At the end, the stack will be the result.
Solution
1 | |
Week 4: January 22nd - January 28th
One Edit Distance
Given two strings s and t, return true if they are both one edit distance apart, otherwise return false.
A string s is said to be one distance apart from a string t if you can:
Insert exactly one character into s to get t.
Delete exactly one character from s to get t.
Replace exactly one character of s with a different character to get t.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Constraints:
-
0 <= s.length <= 10^4 -
0 <= t.length <= 10^4 -
sandtconsist of lower-case letters, upper-case letters and/or digits.
Explanation
-
First, we can check the difference of both strings’ length, if the difference is more than 1, then we can return false immediately.
-
Let’s assume that
sis always shorter or the same length ast. If not, we can callisOneEditDistance(t, s)to inverse the string order. -
Loop through every character of
sand compare tot. If we find a different character, then we have 2 situations. One is both strings have the same length, then we can just returns[i+1:] == t[i+1:]. Another situation isshas one character less thant, then we can just returns[i:] == t[i+1:]. If we don’t find any different character after loopings, thentmust be have one character append to the end ofsin order to be true. For examples = abcandt = abcd, so we can returnlen(s) + 1 == len(t).
Solution
1 | |
Determine if Two Strings Are Close
Two strings are considered close if you can attain one from the other using the following operations:
- Operation 1: Swap any two existing characters.
- For example,
abcde -> aecdb
- For example,
- Operation 2: Transform every occurrence of one existing character into another existing character, and do the same with the other character.
- For example,
aacabb -> bbcbaa(alla’s turn intob’s, and allb’s turn intoa’s)
- For example,
You can use the operations on either string as many times as necessary.
Given two strings, word1 and word2, return true if word1 and word2 are close, and false otherwise.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Constraints:
-
1 <= word1.length, word2.length <= 10^5 -
word1andword2contain only lowercase English letters.
Hint 1:
Operation 1 allows you to freely reorder the string.
Hint 2:
Operation 2 allows you to freely reassign the letters’ frequencies.
Explanation
-
If
word1andword2have different length, we can return false immediately. -
If we only allow to perform operation 1, then
word1andword2must have the same frequency of same characters. -
Now considering operation 2, after we transform characters, the frequency value is still the same, the frequency position is just swapped. For example,
aacabb, frequency fora,b,care[3, 2, 1]; after transform, we havebbcbaa, frequency fora,b,care[2, 3, 1]. So ifword1andword2are formed by the same frequency values, then we can return true.
Solution
1 | |
Sort the Matrix Diagonally
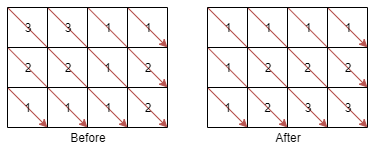
A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix’s end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].
Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
m == mat.length -
n == mat[i].length -
1 <= m, n <= 100 -
1 <= mat[i][j] <= 100
Hint 1:
Use a data structure to store all values of each diagonal.
Hint 2:
How to index the data structure with the id of the diagonal?
Hint 3:
All cells in the same diagonal (i,j) have the same difference so we can get the diagonal of a cell using the difference i-j.
Explanation
-
Values on the same diagonal have the same pattern
diff = r - c, in other word, all values that are on the same diagonal have the same difference when their row index minus column index. -
We can use a hashmap to store the key as
diff = r - c, value will be a priority queue that holds all the values that have the samediff.
Solution
1 | |
Merge k Sorted Lists
You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.
Merge all the linked-lists into one sorted linked-list and return it.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
k == lists.length -
0 <= k <= 10^4 -
0 <= lists[i].length <= 500 -
-10^4 <= lists[i][j] <= 10^4 -
lists[i]is sorted in ascending order. -
The sum of
lists[i].lengthwon’t exceed10^4.
Explanation
-
We can use divide and conquer method to solve this problem. For example, if we have 6
ListNode, then we can solve ListNode1 with ListNode4, ListNode2 with ListNode5, ListNode3 with ListNode6. -
Then, we have 3
ListNodeneed to sort. We then sort ListNode1 with ListNode3. -
Then, we have 2
ListNodeneed to sort. We then sort ListNode1 with ListNode2. -
Finally, we return the result of ListNode1.
-
Since there are $k$ ListNode in the array, similarly to merge sort, we divide $k$ ListNode takes $\log(k)$ time, and there are total of $kn$ nodes to compare, so the total time complexity is $kn\log(k)$. The space complexity is $log(k)$ because of the recursive stack.
Solution
1 | |
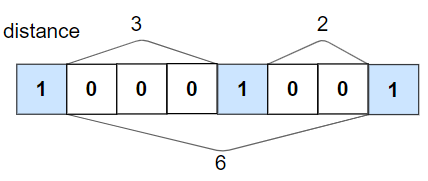
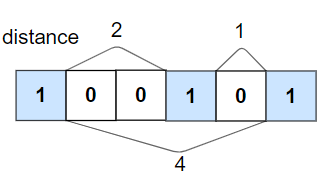
Check If All 1’s Are at Least Length K Places Away
Given an array nums of 0s and 1s and an integer k, return True if all 1’s are at least k places away from each other, otherwise return False.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Constraints:
-
1 <= nums.length <= 10^5 -
0 <= k <= nums.length -
nums[i]is0or1
Hint 1:
Each time you find a number 1, check whether or not it is K or more places away from the next one. If it’s not, return false.
Explanation 1
-
We can solve this problem in one-pass by counting the number of zeros in between the “neighbor”
1s. When we iterate to the number equals1, we can reset the counter. -
To bypass the first 1 in the array, we can initalize the counter equals
k.
Solution 1
1 | |
Explanation 2
- We can also two pointer approach, we use a variable
startto mark the previous 1’s index, then when we iterate to a number that is equals to 1, we can use the current index to subtractstartto see if the difference is less than or equals tok, then return false, else resetstartto the current index.
Solution 2
1 | |
Path With Minimum Effort
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route’s effort is the maximum absolute difference in heights between two consecutive cells of the route.
Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Example 1:
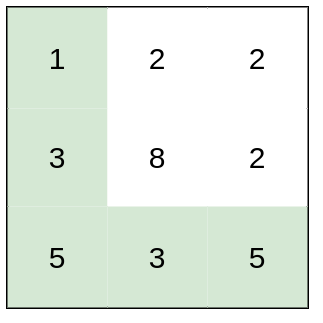
1 | |
Example 2:
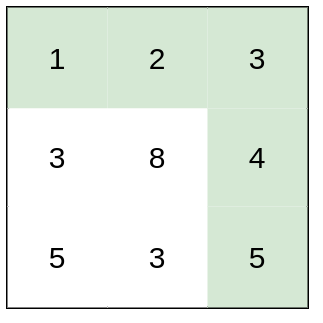
1 | |
Example 3:
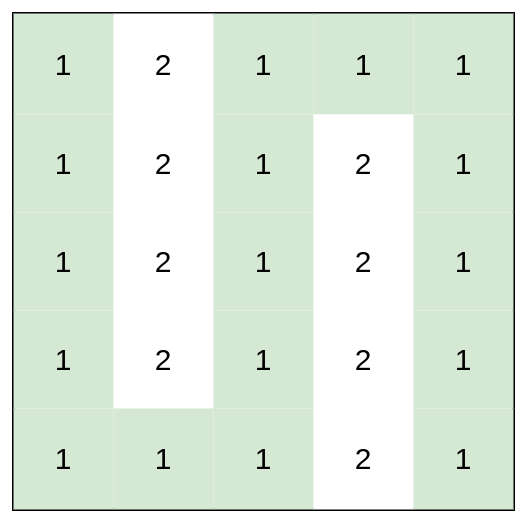
1 | |
Constraints:
-
rows == heights.length -
columns == heights[i].length -
1 <= rows, columns <= 100 -
1 <= heights[i][j] <= 10^6
Hint 1:
Consider the grid as a graph, where adjacent cells have an edge with cost of the difference between the cells.
Hint 2:
If you are given threshold k, check if it is possible to go from (0, 0) to (n-1, m-1) using only edges of ≤ k cost.
Hint 3:
Binary search the k value.
Explanation 1
-
We can solve this problem using Binary Search and BFS. We binary search for a potential result. Based on the constraints
1 <= heights[i][j] <= 10^6the minimum resultleftis 0, the maximum resultrightis 10^6. So whileleft < right, if within the limited effortmid, we can reach the bottom right from top left, then we can updateleft = mid + 1, else we can updateright = mid. -
Now given the
limiteffort, we can use BFS to check we can reach the bottom right. To prevent go back to the same position, we also need a visited array. -
Time complexity:
O(log(MAX_HEIGHT) * m * n), whereMAX_HEIGHT=10^6. Space complexity isO(m * n).
Solution 1
1 | |
Explanation 2
-
We can also use Dijkstra and BFS with PriorityQueue to solve this problem. We initialize a 2d array
efforts[][]to hold every cell’s minimum effort. We know that the effort to reach the top left is 0, for other cells, we can iniitalize the effort to reach them isINT_MAX. First, we calculate the effort to reach the current top left cell’s neighbor cells, and push these cells with its effort into a PriorityQueue. This priority queue will hold integer array as value, this integer array will have length 3, and each index represents[effort, row, col]. The PriorityQueue will sort as the minimumefforton the top of the queue. So each time we poll from the queue, we will always get the cell using the minimum effort to reach. After we poll[effort, row, col], we check if this poll cell is the bottom right cell, if it is, then we can return itseffort. -
Time complexity:
O(E log V), whereEis number of edgesE = 4*M*N,Vis number of veriticesV = M*N, so time complexity equals(ElogV) = O(M*N log M*N), whereMis the number of rows andNis the number of columns in the matrix. Space complexity isO(M * N).
Solution 2
1 | |
Concatenation of Consecutive Binary Numbers
Given an integer n, return the decimal value of the binary string formed by concatenating the binary representations of 1 to n in order, modulo 10^9 + 7.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
1 <= n <= 10^5
Hint 1:
Express the nth number value in a recursion formula and think about how we can do a fast evaluation.
Explanation
-
When we append a new number, we shift the current result
resbylenbit to the left wherelenis the binary representation of the new number, after shifting, we add the current number toresto get the new result. -
To get the length of the new number’s binary representation string, in Java, we can use
Integer.toBinaryString(num).length(). In general, ifnis power of 2, we increaselenby 1. For example,1
2
3
4
5
6
7
8n = 1, len = 1 n = 2, len = 2 n = 3, len = 2 n = 4, len = 3 n = 5, len = 3 n = 6, len = 3 n = 7, len = 3 n = 8, len = 4
We can initialize len = 0, when (n & (n-1)) == 0, we increase len by 1.
Solution
1 | |
Smallest String With A Given Numeric Value
The numeric value of a lowercase character is defined as its position (1-indexed) in the alphabet, so the numeric value of a is 1, the numeric value of b is 2, the numeric value of c is 3, and so on.
The numeric value of a string consisting of lowercase characters is defined as the sum of its characters’ numeric values. For example, the numeric value of the string "abe" is equal to 1 + 2 + 5 = 8.
You are given two integers n and k. Return the lexicographically smallest string with length equal to n and numeric value equal to k.
Note that a string x is lexicographically smaller than string y if x comes before y in dictionary order, that is, either x is a prefix of y, or if i is the first position such that x[i] != y[i], then x[i] comes before y[i] in alphabetic order.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
1 <= n <= 10^5 -
n <= k <= 26 * n
Hint 1:
Think greedily.
Hint 2:
If you build the string from the end to the beginning, it will always be optimal to put the highest possible character at the current index.
Explanation
- First creating a character array with length
nand fill with alla, so now thekbecomesk - n. Whilekis greater than 0, then we start updating from the last character, we wanna increase the last character bymin(25, k), then updatek = k - min(25, k), and move to update the second last character in the next iteration.
Solution
1 | |
Week 5: January 29th - January 31st
Number Of Corner Rectangles
Given a grid where each entry is only 0 or 1, find the number of corner rectangles.
A corner rectangle is 4 distinct 1s on the grid that form an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1s used must be distinct.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Note:
-
The number of rows and columns of
gridwill each be in the range[1, 200]. -
Each
grid[i][j]will be either0or1. -
The number of
1s in the grid will be at most6000.
Hint 1:
For each pair of 1s in the new row (say at new_row[i] and new_row[j]), we could create more rectangles where that pair forms the base. The number of new rectangles is the number of times some previous row had row[i] = row[j] = 1.
Explanation
- If there are two
1s in the same row, in other words,colStart == 1 && colEnd == 1, that is a valid base. Then fix thecolStartandcolEnd, we loop every row, count for the number of valid basenumBase. If there are 2 valid base, then there is 1 rectangle; if there are 3 valid base, then there are 1 + 2 rectangles; if there are 4 valid base, then there are 1 + 2 + 3 rectangles.
Solution
1 | |
Vertical Order Traversal of a Binary Tree
Given the root of a binary tree, calculate the vertical order traversal of the binary tree.
For each node at position (row, col), its left and right children will be at positions (row + 1, col - 1) and (row + 1, col + 1) respectively. The root of the tree is at (0, 0).
The vertical order traversal of a binary tree is a list of top-to-bottom orderings for each column index starting from the leftmost column and ending on the rightmost column. There may be multiple nodes in the same row and same column. In such a case, sort these nodes by their values.
Return the vertical order traversal of the binary tree.
Example 1:
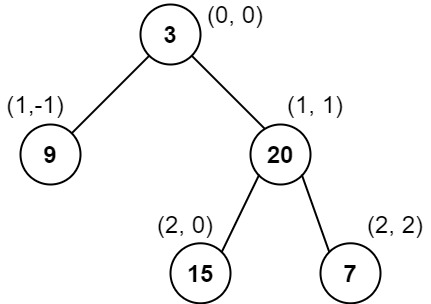
1 | |
Example 2:
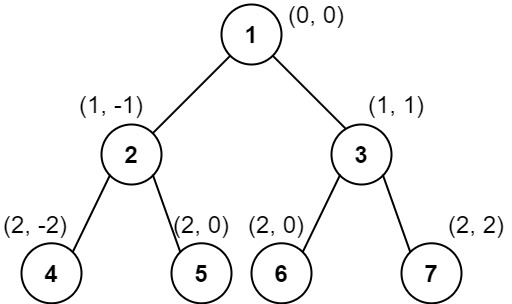
1 | |
Example 3:
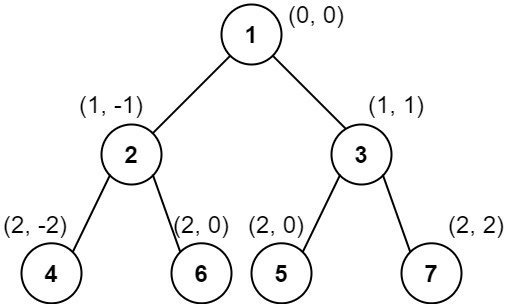
1 | |
Constraints:
-
The number of nodes in the tree is in the range
[1, 1000]. -
0 <= Node.val <= 1000
Explanation
-
We can create a list and store all nodes with their corresponding row and column, in other words,
lst[i] = [row, col, nodeVal]. Then sort this list base on smallest column first, if same column, then sort by their row and smaller row first, otherwise same column and row, then smallest number first. -
Next, iterate the list, push the current element’s
nodeValinto a sublist, if the current element’s column is different from the next element’s column, then we push this sublist into the result list.
Solution
1 | |
Minimize Deviation in Array
You are given an array nums of n positive integers.
You can perform two types of operations on any element of the array any number of times:
- If the element is even, divide it by
2.- For example, if the array is
[1,2,3,4], then you can do this operation on the last element, and the array will be[1,2,3,2].
- For example, if the array is
- If the element is odd, multiply it by
2.- For example, if the array is
[1,2,3,4], then you can do this operation on the first element, and the array will be[2,2,3,4].
- For example, if the array is
The deviation of the array is the maximum difference between any two elements in the array.
Return the minimum deviation the array can have after performing some number of operations.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
n == nums.length -
2 <= n <= 10^5 -
1 <= nums[i] <= 10^9
Hint 1:
Assume you start with the minimum possible value for each number so you can only multiply a number by 2 till it reaches its maximum possible value.
Hint 2:
If there is a better solution than the current one, then it must have either its maximum value less than the current maximum value, or the minimum value larger than the current minimum value.
Hint 3:
Since that we only increase numbers (multiply them by 2), we cannot decrease the current maximum value, so we must multiply the current minimum number by 2.
Explanation
-
The deviation is equal to the maximum number minus the minimum number.
-
Even number never increase.
-
We can double all odd numbers, so they become even numbers. Then we only need to care about the division operation. Now, we only need to decrease the largest number when it’s even.
-
Double odd numbers and put all numbers into a max heap. Track the smallest number. Track the minimum difference between the top of the heap and the smallest number. While the top of the heap is even, remove it, divide, and put back to the heap.
Solution
1 | |
Next Permutation
Implement next permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such an arrangement is not possible, it must rearrange it as the lowest possible order (i.e., sorted in ascending order).
The replacement must be in place and use only constant extra memory.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Constraints:
1 <= nums.length <= 100
0 <= nums[i] <= 100
Explanation
-
First, we can list out all the permuatations. For example, if input array is
[1, 2, 3]. Then we have:1
2
3
4
5
6
7
8[ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] -
If the input array elements are in decreasing order, we can just return the reverse array.
-
If the input array elements are not in decreasing order, for example, the input array is
[1, 2, 7, 4, 3, 1], then its next permutation is[1, 3, 1, 2, 4, 7]. -
We can look from the end elment to the beginning of the input array, we find out elements are increasing until we hit the $2$. Then, we still look from the end element to the beginning, we find out $3$ is larger than $2$. Then, we swap these two elements. Finally, we reverse all the elements starts from the index that is equal to the original input $2$’s index plus one.
1
2
3[1, 2, 7, 4, 3, 1] //swap 2 and 3 [1, 3, 7, 4, 2, 1] //reverse all elements after 3 [1, 3, 1, 2, 4, 7] //result
Solution
1 | |