Still working from home, let’s pratice more Leetcode problems for July LeetCoding Challenge.
Week 1: July 1st - July 7th
Arranging Coins
You have a total of n coins that you want to form in a staircase shape, where every k-th row must have exactly k coins.
Given n, find the total number of full staircase rows that can be formed.
n is a non-negative integer and fits within the range of a 32-bit signed integer.
Example 1:
1 | |
Example 2:
1 | |
Explanation
- We can also use binary search to solve this problem. Initialize
left = 1,right = n,midis therowwe guess. From row 1 to rowmidinclusive, there are totalmid * (mid+1)/2elements. Whileleft <= right. If thesum == n, we returnmidrows; else ifsum < n, then we updateleft = mid + 1; else ifsum > n, then we updateright = mid -1. So outside the while loop, we returnright.
Solution
1 | |
Binary Tree Level Order Traversal II
Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).
For example:
Given binary tree [3,9,20,null,null,15,7],
1 |
|
return its bottom-up level order traversal as:
1 | |
Explanation
- Similar to 102. Binary Tree Level Order Traversal. This time, instead of adding the sublist to the end of the result list, we should add the sublist at the beginning of the result list.
Solution
1 | |
Prison Cells After N Days
There are 8 prison cells in a row, and each cell is either occupied or vacant.
Each day, whether the cell is occupied or vacant changes according to the following rules:
-
If a cell has two adjacent neighbors that are both occupied or both vacant, then the cell becomes occupied.
-
Otherwise, it becomes vacant.
(Note that because the prison is a row, the first and the last cells in the row can’t have two adjacent neighbors.)
We describe the current state of the prison in the following way: cells[i] == 1 if the i-th cell is occupied, else cells[i] == 0.
Given the initial state of the prison, return the state of the prison after N days (and N such changes described above.)
Example 1:
1 | |
Example 2:
1 | |
Note:
-
cells.length == 8 -
cells[i]is in{0, 1} -
1 <= N <= 10^9
Explanation
-
We notice that from day 1, the first index and the last index will always be 0, and only the middle 6 numbers will always be changed. Since the each element can only be either 0 or 1, the total possibility of the middle 6 elements will be 2^6=64. No matter how large the N is, it will have the chance to repeat. We can even reduce from these 64 possibilities further. Among these 64 possibilities, only the possibility that satisfy two adjacent neighbors are same, then the middle number will be 1, else the middle number will be 0. For example,
(0)111000(0)is not satisfy this requirement, in other words, we will not have the chance to transform the array to this number. So the total possibility array that we can transform the input array to is far less than 64. -
Now we know that there is a chance of repeating transform the same cells array, we can use a HashMap to store the key as the cell array in string representation, the value is the current
iday. Loopifrom day 0 toN-1inclusive, if the HashMap contains the key of theiday’s array, that means we are repeating to transform the same cell array. We can calculate the loop lengthloopLen = i - hm[array]. Since in day 0, we may start from an invalid array like(0)111000(0), we can’t just returnprisonAfterNDays(cells, N % loopLen), instead, we returnprisonAfterNDays(cells, (N-i) % loopLen). -
If the HashMap does’t contains the current array as the key, then we brute force to transform the cell array. Initialize
pre= 0, Loopjfrom 1 to 6 inclusive,next = cells[j + 1],cur = cells[j], then updatecells[j]to 1 ifpre == nextelse 0,pre = cur.
Solution
1 | |
Ugly Number II
Write a program to find the n-th ugly number.
Ugly numbers are positive numbers whose prime factors only include 2, 3, 5.
Example:
1 | |
Note:
-
1is typically treated as an ugly number. -
ndoes not exceed 1690.
Hint 1:
The naive approach is to call isUgly for every number until you reach the nth one. Most numbers are not ugly. Try to focus your effort on generating only the ugly ones.
Hint 2:
An ugly number must be multiplied by either 2, 3, or 5 from a smaller ugly number.
Hint 3:
The key is how to maintain the order of the ugly numbers. Try a similar approach of merging from three sorted lists: L1, L2, and L3.
Hint 4:
Assume you have Uk, the kth ugly number. Then Uk+1 must be Min(L1 * 2, L2 * 3, L3 * 5).
Explanation
-
Ugly number is equal to ugly number multiple by ugly number.
-
First we initialize 3 index pointers
(ptrInd2, ptrInd3, ptrInd5)pointing to index 0. We know that in index 0, the number is 1, which is the first ugly number. -
Then, the next ugly number will be the minimum of
min(res[ptrInd2]*2, res[ptrInd3]*3, res[ptrInd5]*5)., which ismin(1*2, 1*3, 1*5), so the minimum is 2, then we add 2 to be the next ugly number, then we increaseptrInd2by 1, nowptrInd2=0+1=1. Since the oldptrInd2multiple by 2 is already added to the result list, we don’t want it in the future. Similarly, if the min is1*3, we increase theptrInd3by 1, same asptrInd5. -
When the size of the result list is
n, we finish the loop, and resturn the last element of the result list.
Solution
1 | |
Hamming Distance
The Hamming distance between two integers is the number of positions at which the corresponding bits are different.
Given two integers x and y, calculate the Hamming distance.
Note:
0 ≤ x, y < 231.
Example:
1 | |
Explanation
-
The problem asks us to find the number of different bit between these two numbers. We can use XOR these two numbers and get the result
a. Ina’s binary form, the number of bit1is the number of different bits betweenxandy. In other words, this problem asks us to find the number of set bits inx XOR y. -
We can do
a AND 1to get the most right bit. If the result is 1, then the right most bit ofais 1. If the result is 0, then the right most bit ofais 0.
Solution
1 | |
Plus One
Given a non-empty array of digits representing a non-negative integer, plus one to the integer.
The digits are stored such that the most significant digit is at the head of the list, and each element in the array contain a single digit.
You may assume the integer does not contain any leading zero, except the number 0 itself.
Example 1:
1 | |
Example 2:
1 | |
Explanation
-
Loop through the array from the last index element, if it is less than 9, then we can add one to it, and return;
1
[1, 2, 3] => [1, 2, 4] -
Else if it is 9, then we set this element to 0, and continue to check the next element.
1
[1, 2, 9] => [1, 3, 0] -
After the loop, meanning that it’s still not returning and the first index element is 0. Then, we create a new array have the first element set to 1, and starts from the second elment, it has all the same elements as the digits array.
1
[9, 9, 9] => [1, 0, 0, 0]
Solution
1 | |
Island Perimeter
You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 represents water.
Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn’t have “lakes” (water inside that isn’t connected to the water around the island). One cell is a square with side length 1. The grid is rectangular, width and height don’t exceed 100. Determine the perimeter of the island.
Example:
1 | |
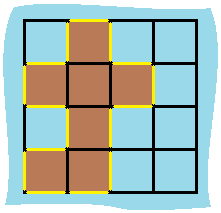
Explanation 1
-
We can loop through all cells. For each cell, if the cell is 0, then we ignore it. If the cell is 1, then we check this cell’s 4 sides: top, bottom, left, right cell.
-
If it doens’t have top cell, that means this cell’s top line is on the edge, so we add 1 to
res; or this cell’s top cell is 0, then we add 1 tores. Then, we check bottom current cell’s bottom cell. If it doesn’t have bottom cell or its bottom cell is 0, then we add 1 tores. Similarlly for current cell’s left and right cells.
Solution 1
1 | |
Explanation 2
- For each cell that is 1, we can first add 4 to
res. Then check the current cell’s top cell, if the top cell is also 1, we subtractresby 2. Also we check the current cell’s left cell, if the left cell is also 1, we subtractresby 2.
Solution 2
1 | |
Week 2: July 8th - July 14th
3Sum
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example:
1 | |
Hint 1:
So, we essentially need to find three numbers x, y, and z such that they add up to the given value. If we fix one of the numbers say x, we are left with the two-sum problem at hand!
Hint 2:
For the two-sum problem, if we fix one of the numbers, say
1 | |
, we have to scan the entire array to find the next number
1 | |
which is
1 | |
where value is the input parameter. Can we change our array somehow so that this search becomes faster?
Hint 3:
The second train of thought for two-sum is, without changing the array, can we use additional space somehow? Like maybe a hash map to speed up the search?
Explanation
-
Sort the array.
-
If the first element is greater than 0 or the last element is less than 0, we know that we can’t form a 0.
-
Loop through the array start from the first element, we fix the first element, then use two pointers technique to find two elements that sum to targetVal-fixVal until break out the left < right condition. While looping, we need to ignore the same fix number and left and right values.
-
We can actually convert this problem to a nSum problem.
Solution
1 | |
Maximum Width of Binary Tree
Given a binary tree, write a function to get the maximum width of the given tree. The width of a tree is the maximum width among all levels. The binary tree has the same structure as a full binary tree, but some nodes are null.
The width of one level is defined as the length between the end-nodes (the leftmost and right most non-null nodes in the level, where the null nodes between the end-nodes are also counted into the length calculation.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Example 4:
1 | |
Note: Answer will in the range of 32-bit signed integer.
Explanation
-
Another BFS method is to make a custom class
NodeIdxwith property TreeNode and the position of the node. If the root node position is 0, then its left child has position 0 * 2 + 1, its right child has position 0 * 2 + 2 = 2. -
In BFS, we need to create a queue to hold the current level’s TreeNodes and their position. So we can calculate the current level’s width as
queue.getFirst().idx; - queue.getLast().idx;. -
Initially, we put the root node and its position
0to the queue. While the queue is not empty, we calculate the width using step2’s method. Then pop the current level’s nodes and push their left child and right child with their respective position to the queue. Repeat step 2 and step 3 until the queue is empty. -
Return the maximum width.
Solution
1 | |
Flatten a Multilevel Doubly Linked List
You are given a doubly linked list which in addition to the next and previous pointers, it could have a child pointer, which may or may not point to a separate doubly linked list. These child lists may have one or more children of their own, and so on, to produce a multilevel data structure, as shown in the example below.
Flatten the list so that all the nodes appear in a single-level, doubly linked list. You are given the head of the first level of the list.
Example 1:
1 | |
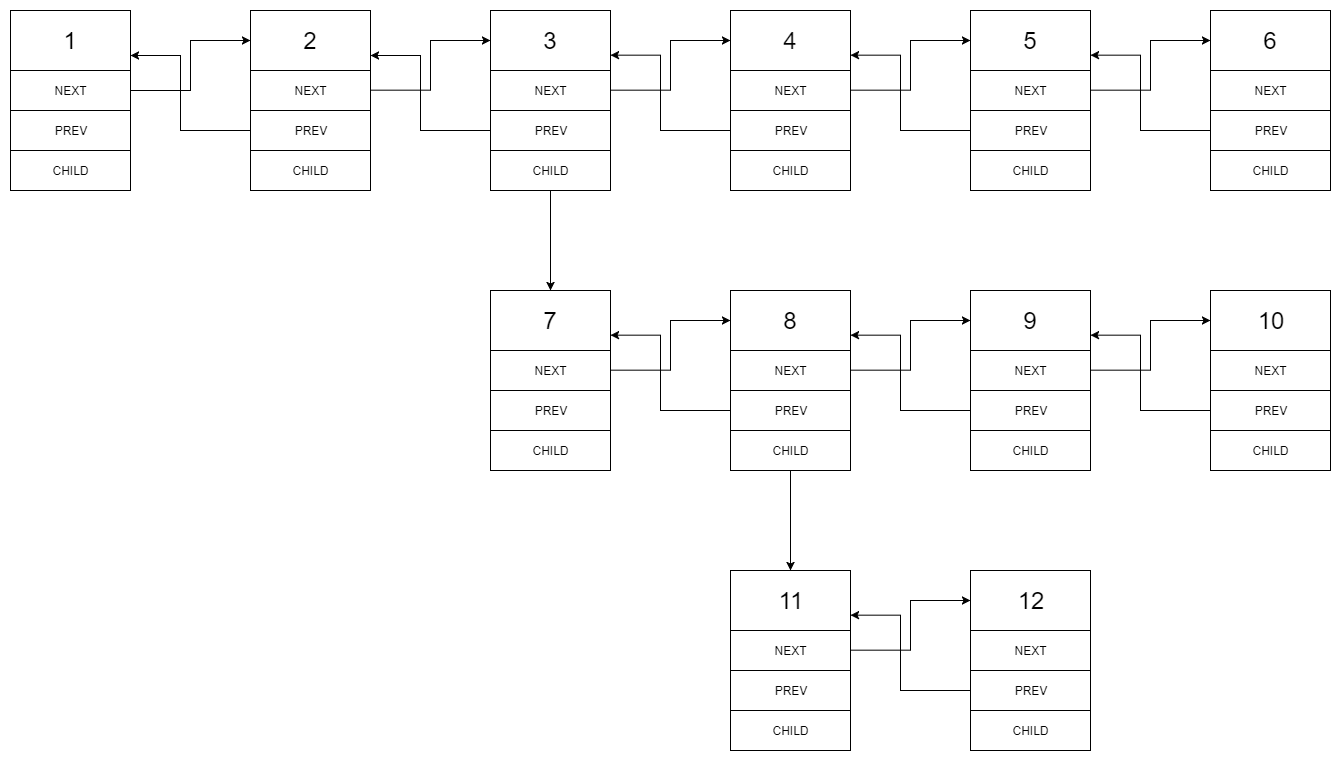
1 | |

Example 2:
1 | |
Example 3:
1 | |
How multilevel linked list is represented in test case:
We use the multilevel linked list from Example 1 above:
1 | |
The serialization of each level is as follows:
1 | |
To serialize all levels together we will add nulls in each level to signify no node connects to the upper node of the previous level. The serialization becomes:
1 | |
Merging the serialization of each level and removing trailing nulls we obtain:
1 | |
Constraints:
-
Number of Nodes will not exceed 1000.
-
1 <= Node.val <= 10^5
Explanation
-
We can make a flattern helper function to return the last node of the child list so we don’t need to iterat to the last node. We need the last node because we want to connect current node’s child list’s last node with current node’s next node
lastNode.next = cur.next. -
We pass the
headnode to the helper function. Inside the helper function, we create two pointerscurandtail. Whilecur != NULL, we record current node’s next node and child node asnextandchildrespectively. -
If
childis not NULL, we recursively call the helper function withchildas the argument. We updatetailto be this recursive helper function’s return node. Then, we connecttailwithnext. Then connectcurandchild. Then updatecur.childis NULL. Then we updatecur = tailso we don’t need to iterate all child list’s node. -
If
childis NULL, we simply updatetailto becurandcurbenext. At the end, returntail.
Solution
1 | |
Subsets
Given a set of distinct integers, nums, return all possible subsets (the power set).
Note: The solution set must not contain duplicate subsets.
Example:
1 | |
Explanation 1
-
Backtracking.
-
The output is:
[[],[1],[1,2],[1,2,3],[1,3],[2],[2,3],[3]].
Solution 1
1 | |
Explanation 2
- Recursive method.
1 | |
Solution 2
1 | |
Explanation 3
- Iterative method.
1 | |
Solution 3
1 | |
Reverse Bits
Reverse bits of a given 32 bits unsigned integer.
Example 1:
1 | |
Example 2:
1 | |
Note:
-
Note that in some languages such as Java, there is no unsigned integer type. In this case, both input and output will be given as signed integer type and should not affect your implementation, as the internal binary representation of the integer is the same whether it is signed or unsigned.
-
In Java, the compiler represents the signed integers using 2’s complement notation. Therefore, in Example 2 above the input represents the signed integer
-3and the output represents the signed integer-1073741825.
Follow up:
If this function is called many times, how would you optimize it?
Explanation
-
Loop through 32 times. In each iteration, left shift
res. -
Get the right most bit using
n & 1and add it tores. -
Right shift
n. -
Outside the loop, return
res.
Solution
1 | |
Same Tree
Given two binary trees, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical and the nodes have the same value.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Explanation 1
-
We can use recursion method to solve this problem. If two tree are the same, then their
root.valare the same, androot.left.valare the same, androot.right.valare the same. -
The base case is if two trees are NULL, then they are the same, else if one tree is NULL another is not NULL, then we return false.
Solution 1
1 | |
Explanation 2
-
We can also use BFS (level-order traversal) to solve this problem. The difference is we can’t pop the nodes from both queue and compare them because in the problem’s Example 2, the second level have the same values
2, but one of them is belongs to the left child, and another one belongs to the right child. So before we push the node into the queue, we need to compare both current nodes’ left childs and right childs. -
First, we make a helper function to compare 2 root nodes if they both are NULL or they both have the same value, then return true, else return false.
-
Initialize two queues
q1to hold the TreeNodes for Treep,q2to hold the TreeNodes for Treeq. Then, we push root nodeptoq1and push root nodeqtoq2. -
While both queue are not empty, we poll out the nodes
curPandcurQfrom both queues. Then we pass their left childs to the helper function, and pass their right childs to the helper function to comparecurP.leftis the same ascurQ.left, andcurP.rightis the same ascurQ.right. If one of the helper function return false, we immediately return false. Else, we push their left child and right child to the queue. Repeat until one of the queue is empty. -
Outside the while loop, we can return true.
Solution 2
1 | |
Angle Between Hands of a Clock
Given two numbers, hour and minutes. Return the smaller angle (in degrees) formed between the hour and the minute hand.
Example 1:
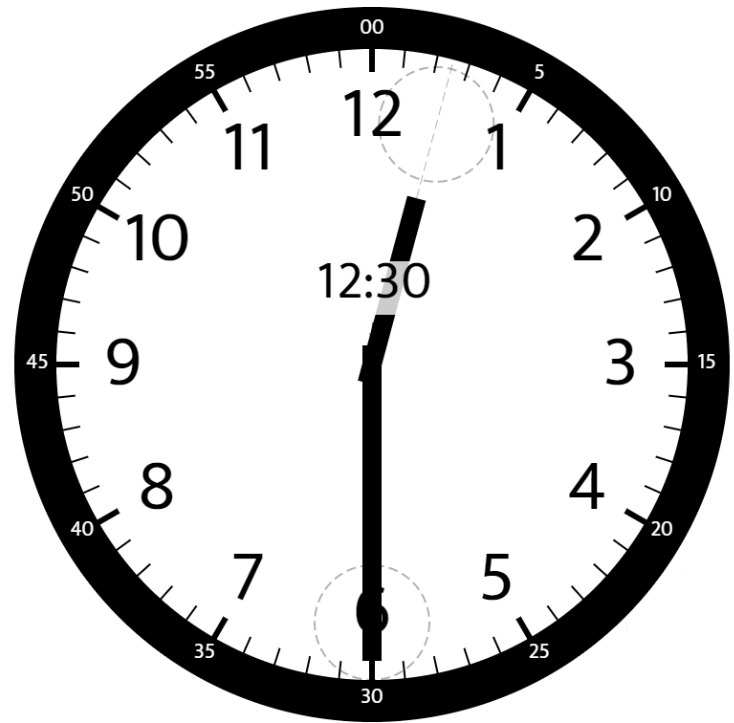
1 | |
Example 2:
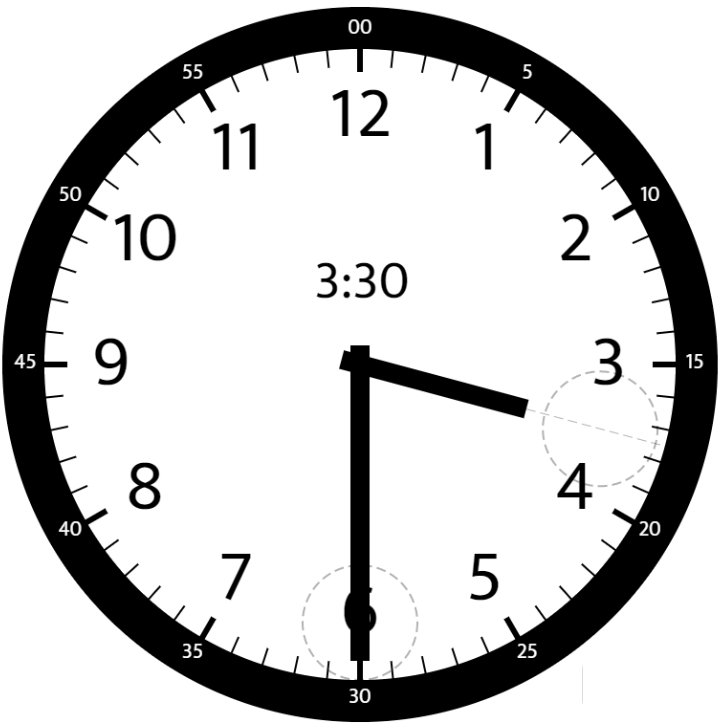
1 | |
Example 3:
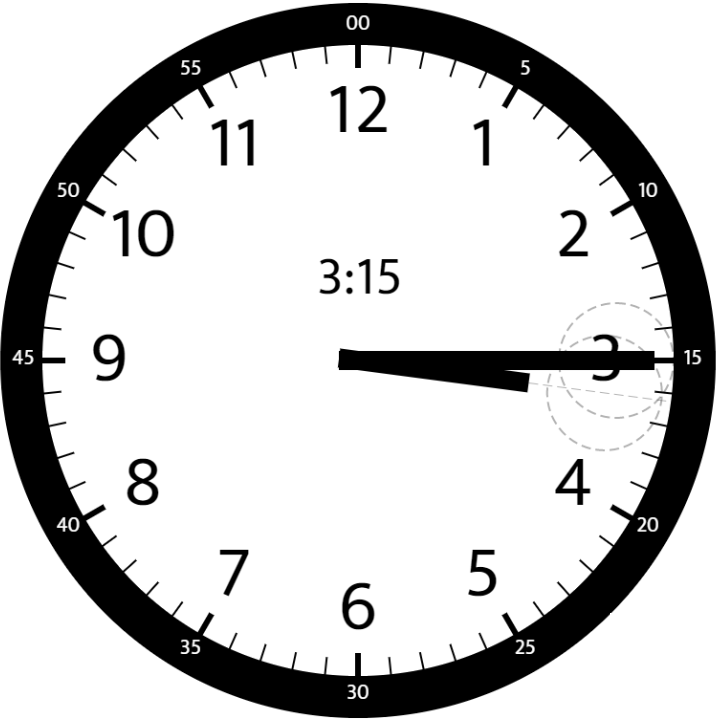
1 | |
Example 4:
1 | |
Example 5:
1 | |
Constraints:
-
1 <= hour <= 12 -
0 <= minutes <= 59
Answers within 10^-5 of the actual value will be accepted as correct.
Hint 1:
The tricky part is determining how the minute hand affects the position of the hour hand.
Hint 2:
Calculate the angles separately then find the difference.
Explanation
-
We know that one hour has 30 degree and one minute has 5 degree, so we need to count how many hour and minute we have. The angel will be the difference between minute degree and hour degree.
-
If
houris 12, it’s the same as 0, so we can updatehour = hour % 12. We know that 30 minutes is 0.5 hour, so the total hour we has istotalHour = hour % 12 + (float)minutes/60. Then we can calculate the hour degree istotalHour * 30. The total minute is the same as the input minute, so the minute degree isminutes * 6. -
The angel degree
resis equal to the absolute value of the difference between minute degree and hour degree. The result will be the minimum betweenresand360-res.
Solution
1 | |
Week 3: July 15th - July 21st
Reverse Words in a String
Given an input string, reverse the string word by word.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Note:
-
A word is defined as a sequence of non-space characters.
-
Input string may contain leading or trailing spaces. However, your reversed string should not contain leading or trailing spaces.
-
You need to reduce multiple spaces between two words to a single space in the reversed string.
Follow up:
For C programmers, try to solve it in-place in O(1) extra space.
Explanation 1
- If we do this problem without programming, first we would split each word no matter how many spaces in between each word. We can use
strings.Fieldsto get all the words into an array, then reverse this array, and finally usestrings.Jointo convert this array back to string.
Solution 1
1 | |
Explanation 2
-
We can create two pointers
startandendpoint to a word’s beginning index and end index (exclusive), and definenis the length of the string. -
While
start < n && s[start] == ' ', then we keep increasestart. Now,startis pointing to the beginning of the word. Then updateend = start + 1, whileend < n && s[end] != ' ', then we keep increaseend. Now,endis pointing to the ending of the word (exlusive). -
If
resis empty, we simply updaterestos[start, end]. Else, we appends[start, end] + " "to the beginning of theres. After updatingres, we then updatestart = end + 1. Repeat step 2 and step 3 whilestart < n. Ifstartis equal ton, we need to stop and return the result.
Solution 2
1 | |
Pow(x, n)
Implement pow(x, n), which calculates x raised to the power n (xn).
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Note:
-
-100.0 < x < 100.0
-
n is a 32-bit signed integer, within the range [−231, 231 − 1]
Explanation
-
Let’s see an example first, $2^4 = 4^2 = 16^1$.
-
We can divide the
powerby 2 and multiple thebaseby itself untilpoweris 1. -
Default the
resequal 1, if thepoweris an odd number, we can multiple theresby base, then power subtract 1 to become even. -
If
poweris a negative number, we can revertpowerto positive then after we get the finalres, we use 1 to divide theres. -
The corner case is the minimum of integer is
-2147483648and the maximum of integer is2147483647, which is 1 less than the revert of minimum integer. In order to fix it, before we revert the negativepower, we add 1 to it, andresmultiple by thebasebecause $-2147483648 + 1 = -2147483647$, when we revert it can be a maximum integer now, but we multiple the base one time less, so that is why we multiple theresbybase.
Solution
1 | |
Top K Frequent Elements
Given a non-empty array of integers, return the k most frequent elements.
Example 1:
1 | |
Example 2:
1 | |
Note:
-
You may assume k is always valid, 1 ≤ k ≤ number of unique elements.
-
Your algorithm’s time complexity must be better than O(n log n), where n is the array’s size.
-
It’s guaranteed that the answer is unique, in other words the set of the top k frequent elements is unique.
-
You can return the answer in any order.
Explanation 1
-
First, create a hashmap to store the number and its frequency.
-
Next, create a min heap or priority queue, loop through the hashmap, store the hashmap’s entry into the priority queue, and sort by the entry’s value. If the queue has size more than
k, we can poll. Since it’s a min heap, the poll entry will be the smallest entry value or frequency. -
Now our queue has the
kmost frequency entry. We can loop through the queue, poll them out add into areslist. Now ourreslist will have frequency from smallest to largest. At the end, we can reverse thereslist and return it.
Solution 1
1 | |
Explanation 2
-
We can use bucket sort with $O(n)$ runtime to solve this problem.
-
First, we create a hashmap to store each number and its frequency. Then, we find out the maximum frequency, and use the maximum frequency as the length of a new array. The array will have length maximum frequency plus one, since we want the maximum frequency is the last index of this array.
-
Each array element will be a new array list. Then, we loop through the HashMap, put the entry’s frequency as the array’s index, number will add it to the list
arr[i]. -
Now, we can loop from the back of the array to front, for each arraylist
arr[i], we store their number into ourreslist until thereslist has sizek.
Solution 2
1 | |
Course Schedule II
There are a total of n courses you have to take, labeled from 0 to n-1.
Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]
Given the total number of courses and a list of prerequisite pairs, return the ordering of courses you should take to finish all courses.
There may be multiple correct orders, you just need to return one of them. If it is impossible to finish all courses, return an empty array.
Example 1:
1 | |
Example 2:
1 | |
Note:
-
The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
-
You may assume that there are no duplicate edges in the input prerequisites.
Hint 1:
This problem is equivalent to finding the topological order in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses.
Hint 2:
Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort.
Hint 3:
Topological sort could also be done via BFS.
Explanation 1
-
We can solve this problem by topological sort. First, loop through the
edges, create an adjacent list which is prerequisite course points to target course. Also create an arrayinDegree[i]to record the number of prerequisite course that courseihas. -
Loop through all the courses, if course
idoesn’t need any prerequisite, in other word,inDegree[i]is 0, then we push this course to the queue. -
While the queue is not empty, we pop one course
curout. Put this course to the result list. Loop through this course’s neighbor course, and subtract each neighbor’s prerequisite or inDegree by 1. If any neighbor course’s inDegree is 0, then we push it to the queue. -
If the result list has the size of
numCourses, then we return this result list. Otherwise, we can’t finish all the course, so return an empty result.
Solution 1
1 | |
Explanation 2
-
We can also use DFS topological sort to solve this problem. First, create an adjacent list which is prerequisite course points to target course. In the main function, loop through all the courses. Each iteration, we pass the current course into the helper function.
-
In the helper function, we DFS the current course’s deepest target course, then push this deepest target course into the stack. At the end, we return the reverse stack’s courses as the result.
-
We also need to create an array
visitedto have cycle detection. For example, initiallyvisited[i] = 0means courseiis unvisited; ifvisited[i] = -1that means courseiis visiting and not finish; ifcourse[i] = 1that means courseiis finish visiting. If there’s a cycle, we returnfalsefrom the helper function. In the main function, if the we gotfalsefrom the helper function, then we return an empty result.
Solution 2
1 | |
Add Binary
Given two binary strings, return their sum (also a binary string).
The input strings are both non-empty and contains only characters 1 or 0.
Example 1:
1 | |
Example 2:
1 | |
Constraints:
-
Each string consists only of
'0'or'1'characters. -
1 <= a.length, b.length <= 10^4 -
Each string is either
"0"or doesn’t contain any leading zero.
Explanation
-
Similar to 2. Add Two Numbers. First, we need to create a stringbuilder
resto hold the result. We need a pointer pointing at the end index of stringA, and another pointer pointing at the end index of stringB because we add these two numbers starting from the least significant digit. -
While either of the pointer is not negative, We can create a
sumto hold the sum of two digit each time we add, and initialize the this sum equal tocarry, wherecarryinitialize to 0 before we start calculating. -
After adding two digits to the sum, now the result digit’s value will be
sum % 2and we added it to the stringbuilder, and carry will besum / 2. Repeat this while loop. -
Outside of the while loop, if the
carryis not zero, then we append it to theres, and we reverse theresand return its string representation.
Solution
1 | |
Remove Linked List Elements
Remove all elements from a linked list of integers that have value val.
Example:
1 | |
Explanation 1
-
Iterative method way. While the
headis not NULL andhead.valequalsval, then we moveheadforward. If theheadis NULL, then we return NULL. -
Create a previous pointer
preandpre.next = head, and create a current pointercurpoints tohead. Whilecuris not NULL, we check ifcur.val != val, then we updatepre = cur. Else ifcur.val == val, then we updatepre.next = cur.next. Both condition, we updatecur = cur.next. -
At the end, we return
head.
Solution 1
1 | |
Explanation 2
-
Recursive way. While the
headis not NULL andhead.valequalsval, then we moveheadforward. If theheadis NULL, then we return NULL. -
Recursivly call the main function with
head.nextand the inputval, then updatehead.nextto this recursive function;s return value. -
At the end, return
head.
Solution 2
1 | |
Word Search
Given a 2D board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example:
1 | |
Constraints:
-
boardandwordconsists only of lowercase and uppercase English letters. -
1 <= board.length <= 200 -
1 <= board[i].length <= 200 -
1 <= word.length <= 10^3
Explanation
-
First, we can iterate the board and find the character that is matched with the first character of the word. Then, think of this character as the middle, we recursivly check its top, bottom, left, right element if match with the second character of the word.
-
Special case is we cannot use the same character twice, so we create a
isUsedtable that have the same size as the board. If the character is used, then we mark it as true in theisUsedtable. Or if the current word match, then we mark the current word as a random character such as#, after the recursive function, we backtrack the current word to its original character.
Solution
1 | |
Week 4: July 22nd - July 28th
Binary Tree Zigzag Level Order Traversal
Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).
For example:
Given binary tree [3,9,20,null,null,15,7],
1 |
|
return its zigzag level order traversal as:
1 | |
Explanation 1
-
Similar to 102. Binary Tree Level Order Traversal, but this time we need to add value from left to right, in the next level, we add values from right to left. Then next level, add values from left to right, next level from right to left.
-
When the current level is from left to right, we can normally pop value from the beginning and add its child to the end (left child first). When the current level is from right to left, we pop values from the end and add its child (right child first) to the beginning.
Solution 1
1 | |
Explanation 2
- We can also use DFS to solve this problem. Start from level 0, if the current level is even number, then we add the current root value to the end of sublist
res[level], else add it to the front of the sublistres[level].
Solution 2
1 | |
Single Number III
Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.
Example:
1 | |
Note:
-
The order of the result is not important. So in the above example,
[5, 3]is also correct. -
Your algorithm should run in linear runtime complexity. Could you implement it using only constant space complexity?
Explanation
-
This problem asks us to find the two numbers (let say
aandb) that are appear only once and they are different. If we want to use the XOR method by 136. Single Number, we need to seperate these two numbers into two different groups then apply the XOR method. -
If we XOR all the numbers in the array, then the result will be
xo = a ^ bbecause all other numbers are the same and appear twice and they will eventually become zero. Now, we want to seperate the array into two groups. Note, thexocannot be zero here sinceaandbare different. We can use a bit as a seperate point, which is thexoright most non-zero bit as a seperate point. Becauseaandbon that bit will have different value. Note, the seperate point number will be only that bit is 1, other bit are 0. For example00100. -
We use this seperate number (let say
diff) to AND all the numbers in the array. If the current iterated number AND this seperate number equals 0, then it’s one group; else equal 1, will be another group, sinceaandbon that bit are different. -
We can use the XOR method to find that appeared only once number in a group to find
a, and use the same method to findbin antoher group. -
How do we find
diff? After we XOR all numbers in the array to getxo, we use the formuladiff = ~(xo-1) & xoordiff = (-xo) & xoto getdiff. For example, ifxois 101100, then it subtract one equals 101011, not 101011 equals 010100. Then 010100 AND 101100 becomes 000100, which has only the right most 1 bit ofxo.
Solution
1 | |
All Paths From Source to Target
Given a directed, acyclic graph of N nodes. Find all possible paths from node 0 to node N-1, and return them in any order.
The graph is given as follows: the nodes are 0, 1, …, graph.length - 1. graph[i] is a list of all nodes j for which the edge (i, j) exists.
1 | |
Note:
-
The number of nodes in the graph will be in the range
[2, 15]. -
You can print different paths in any order, but you should keep the order of nodes inside one path.
Explanation
-
We can solve this problem using DFS method.
-
The input is the adjacent list. In the main function, we create a result list, and a current path list, then pass the graph, the result list, the current path list, and the starting node 0 to the helper function.
-
Inside the helper function, we push the current node to the current path list. Then if the current node is the target node, we create a copy of the current path list and add to the result list. Else, we loop through the current node’s neighbors, and call the helper function recursively. At the end of the helper function, we need to backtrack to pop the last element we just added from the current path list.
Solution
1 | |
Find Minimum in Rotated Sorted Array II
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
Find the minimum element.
The array may contain duplicates.
Example 1:
1 | |
Example 2:
1 | |
Note:
-
This is a follow up problem to Find Minimum in Rotated Sorted Array.
-
Would allow duplicates affect the run-time complexity? How and why?
Explanation
-
Similar to 153. Find Minimum in Rotated Sorted Array, this time there’s possibility that
nums[left] == nums[mid] == nums[right], and we don’t know which side of the array need to be check. -
To solve this, we can simply apply the same method as before, but this time, we add one more if condition, if
nums[right] == nums[mid], then we moverightto the left 1 step. This method doesn’t affect our solution since we just remove one repeated number.
Solution
1 | |
Add Digits
Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.
Example:
1 | |
Follow up:
Could you do it without any loop/recursion in O(1) runtime?
Hint 1:
A naive implementation of the above process is trivial. Could you come up with other methods?
Hint 2:
What are all the possible results?
Hint 3:
How do they occur, periodically or randomly?
Hint 4:
You may find this Wikipedia article useful.
Explanation
-
From the below pattern, we know the result will be
num % 9. Special case is ifnum = 9, then the remainder will be 0. To avoid that, we can use a new formula(num-1) % 9 + 1. Now the special case isnum = 0. In C++ and Java,-1 % 9, the quotient is 0, remainder is -1. But in Python, the quotient is -1, remainder is 8. So we can first check ifnum = 0, else apply the new formula.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21num -> res 1 -> 1 2 -> 2 3 -> 3 4 -> 4 5 -> 5 6 -> 6 7 -> 7 8 -> 8 9 -> 9 10 -> 1 11 -> 2 12 -> 3 13 -> 4 14 -> 5 15 -> 6 16 -> 7 17 -> 8 18 -> 9 19 -> 1 20 -> 2
Solution
1 | |
Construct Binary Tree from Inorder and Postorder Traversal
Given inorder and postorder traversal of a tree, construct the binary tree.
Note:
You may assume that duplicates do not exist in the tree.
For example, given
1 | |
Return the following binary tree:
1 |
|
Explanation
-
Similar to 105. Construct Binary Tree from Preorder and Inorder Traversal, this time, we know the root node is the end element of
postorderarray, and we can find the root element in theinorderarray, then we can know the range of leftsubtree and rightsubtree. One example is below:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29Inorder: 11 4 5 13 8 9 Postorder: 11 4 13 9 8 5 11 4 5 13 8 9 => 5 11 4 13 9 8 5 / \ 11 4 13 8 9 => 5 11 4 13 9 8 / \ 4 8 11 13 9 => 5 11 13 9 / \ 4 8 / / \ 11 13 9 -
Using the while loop to find the root value’s index in
inorder[]in each recursion call make the time complexity be $O(n^2)$. We can reduce the time complexity to $O(n)$ by using a HashMap to record the key is the element, value is the element’s index. -
We can also remove the
postStartsince we only need to find the root frompostorder[]by usingpostEnd.
Solution
1 | |
Task Scheduler
You are given a char array representing tasks CPU need to do. It contains capital letters A to Z where each letter represents a different task. Tasks could be done without the original order of the array. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer n that represents the cooldown period between two same tasks (the same letter in the array), that is that there must be at least n units of time between any two same tasks.
You need to return the least number of units of times that the CPU will take to finish all the given tasks.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Constraints:
-
The number of tasks is in the range
[1, 10000]. -
The integer
nis in the range[0, 100].
Explanation
-
In this problem,
nmeans two same tasks must havendifferent tasks or idle in between, so we first seperate the most frequent tasks, then assign the less frequent tasks in the gap of the most frequent tasks. -
For example 1, if we have
tasks = [AAAABBBEEFFGG]andn=3. First, we will seperate theAsince it has the highest frequency, and we fill 3 space in between.1
2
3
4
5A---A---A---A (seperat A with n space in between) AB--AB--AB--A (add B) ABE-ABE-AB--A (add E) ABEFABE-ABF-A (add F, fill it evently) ABEFABEGABFGA (add G) -
Another example 2, we have
tasks = [ACCCEEE]andn=2. Since C and E has the same frequency 3, we can think of CE as a whole, and addn - (mxCnt - 1) = 2 - (2-1) = 1space in between.1
2CE-CE-CE CEACE-CE (add A) -
Notice from the above two examples, we have
maxFreq-1groups, and append the letter that has the most frequency at the end. -
From the above example1, we consider
A---as one group, it appears3=maxFreq-1=4-1times, then add the lastAat the end. The group size is4=n+1=3+1. -
From the above example2, the group
CE-appears2=maxFreq=3-1times, then we add the lastCEat the end. The group size is3=n+1=2+1. -
One corner case is
n = 0. For example, we havetasks = [AAABBB]andn=0. The maximum frequency is 3, so we have2=maxFreq-1=3-1groups likeABAB. The group size is notn+1=0+1=1, instead, it should be 2 in this case. In other words, if then=0, then any tasks can next to each other, so the result will be at least equals to thetasks.length.
Solution
1 | |
Week 5: July 29th - July 31st
Best Time to Buy and Sell Stock with Cooldown
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:
-
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
-
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)
Example:
1 | |
Explanation
-
We can represent this problem in 3 states.
1
2
3
4
5
6
7
8
9
10
11
12
13hold ---- | | v | hold S1 <------S3 \ ^ Buy \ / \ / Sell v / S2 | ^ |__| hold -
We can know that S1 can be only obtained by hold at itself or hold from S2; S2 can be only obtained by rest at itself or buy from S1; S3 can be obtained only by sell stock from S2.
-
So we will have:
1
2
3S1[i] = Math.max(S1[i-1], S3[i-1]); S2[i] = Math.max(S2[i-1], S1[i-1]-prices[i]); S3[i] = S2[i-1] + prices[i]; -
We know that S2 will never be the largest state, because it buy(cost money), and if it hold, it will stay the same and also smaller than S1. So, the maximum state must be either S1 or S3.
-
Base case
1
2
3s0[0] = 0; // At the start, we don't have any stock if we just rest s1[0] = -prices[0]; // After buy, we should have -prices[0] profit. s2[0] = INT_MIN; // At the start, we can't reach this state, can set to 0 or INT_MIN
Solution
1 | |
Word Break II
Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences.
Note:
-
The same word in the dictionary may be reused multiple times in the segmentation.
-
You may assume the dictionary does not contain duplicate words.
Example 1:
1 | |
Example 2:
1 | |
Example 3:
1 | |
Explanation
-
When the question asks to return all different situation, we can usually use recursion to solve it.
-
First, we can think of how we solve it in a manual way. From the above example 1, we will find if any string from the
wordDictcan be the beginning of thes. We can check it using the length of string and ifs[0:stringFromArr.length] == stringFromArr, then thestringFromArrcan be the beginning ofs. In example1, we find out cat and cats both can be the beginning ofs. If we choose cat, thensbecomes “sanddog”. We again find the beginning string from thewordDict, then we find out “sand” also from the beginning of the string, thensbecomes “dog”, and it also inside thewordDict, this mean we find out result string. -
This method can use recursion to solve it because when
sis changed, the way to solve is the same. This is a brute force way, and we are doing repeated work. For example, whensbecomes “sanddog”, we know it can split to “sand” and “dog”. If we face “sanddog” again, then we don’t want to recursive to solve again, we want to save this result. Because we have to savesand the its splitted strings at the same time, then we can use ahashmap<String, List<String>>. -
In the recursion function, the base case will be if the map has key, then we just return the value.
-
In summary, we iterate the
wordDictarray, and check if a stringwordcan be the beginning ofs, then we pass its following string to the recursive function and save the result array asremain. Then, we iterate each result string inremainand concatnatewordto form one string, and push this string to the result array.
Solution
1 | |
Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
1 | |
Example 2:
1 | |
Constraints:
1 <= n <= 45
Hint 1:
To reach nth step, what could have been your previous steps? (Think about the step sizes)
Explanation
-
We can use dynamic programming to solve this problem. The base case is when n = 0, res = 0; when n = 1, res = 1; when n = 2, res = 2.
-
The way to reach the current
istep is equal to the way to reachi-1step plus the way to reachi-2step.
Solution
1 | |