June LeetCoding Challenge

Posted on | In

Continue working from home. It looks like LeetCode will continue this every day problem series. Let’s continue this one day one go problem for June LeetCoding Challenge.

Week 1: June 1st–June 7th

Invert Binary Tree

Invert a binary tree.

Example:

Input:

1
2
3
4
5
     4
   /   \
  2     7
 / \   / \
1   3 6   9

Output:

1
2
3
4
5
     4
   /   \
  7     2
 / \   / \
9   6 3   1

Trivia:

This problem was inspired by this original tweet by Max Howell:

Google: 90% of our engineers use the software you wrote (Homebrew), but you can’t invert a binary tree on a whiteboard so f*** off.

Explanation 1

  1. In a recursive way, we can recursivly swap the left child and right child.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func invertTree(root *TreeNode) *TreeNode {
    if root == nil { return nil }
    temp := root.Left
    root.Left = invertTree(root.Right)
    root.Right = invertTree(temp)
    return root
}

Explanation 2

  1. In a non recursive way, we need to create a queue, and we can swap the left and right child level by level. First, push the root to the queue, while the queue is not empty, poll it out and swap its left and right child. After swapping, push their left and right child to the queue.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func invertTree(root *TreeNode) *TreeNode {
    if root == nil { return nil }

    queue := make([]*TreeNode, 0)
    queue = append(queue, root)

    for len(queue) != 0 {
        curRoot := queue[0]
        queue = queue[1:]
        curRoot.Left, curRoot.Right = curRoot.Right, curRoot.Left
        if curRoot.Left != nil { queue = append(queue, curRoot.Left) }
        if curRoot.Right != nil { queue = append(queue, curRoot.Right) }
    }

    return root
}

Delete Node in a Linked List

Write a function to delete a node (except the tail) in a singly linked list, given only access to that node.

Given linked list – head = [4,5,1,9], which looks like following:

Delete Node in a Linked List

Example 1:

1
2
3
Input: head = [4,5,1,9], node = 5
Output: [4,1,9]
Explanation: You are given the second node with value 5, the linked list should become 4 -> 1 -> 9 after calling your function.

Example 2:

1
2
3
Input: head = [4,5,1,9], node = 1
Output: [4,5,9]
Explanation: You are given the third node with value 1, the linked list should become 4 -> 5 -> 9 after calling your function.

Note:

  • The linked list will have at least two elements.

  • All of the nodes’ values will be unique.

  • The given node will not be the tail and it will always be a valid node of the linked list.

  • Do not return anything from your function.

Explanation

  1. This time we are only giving the node that we want to delete. We can replace this node’s value with node.next.val, and change it’s next pointer to node.next.next.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func deleteNode(node *ListNode) {
    next := node.Next
    node.Val = next.Val
    node.Next = next.Next
    next = nil
}

Two City Scheduling

There are 2N people a company is planning to interview. The cost of flying the i-th person to city A is costs[i][0], and the cost of flying the i-th person to city B is costs[i][1].

Return the minimum cost to fly every person to a city such that exactly N people arrive in each city.

Example 1:

1
2
3
4
5
6
7
8
9
Input: [[10,20],[30,200],[400,50],[30,20]]
Output: 110
Explanation:
The first person goes to city A for a cost of 10.
The second person goes to city A for a cost of 30.
The third person goes to city B for a cost of 50.
The fourth person goes to city B for a cost of 20.

The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.

Note:

  1. 1 <= costs.length <= 100

  2. It is guaranteed that costs.length is even.

  3. 1 <= costs[i][0], costs[i][1] <= 1000

Explanation 1

  1. Assume all people go to city A. From the problem’s example, we have the total cost be 10 + 30 + 400 + 30 = 470.

  2. Now we need to assign half the people to go to city B. If we assign the first person to city B, we increase our total cost by 10. If assign the second person to city B, total cost increase 170. Assign third person to city B, total cost decrease 350. Assign fourth person to city B, total cost decrease 10. In other words, [10, 170, -350, -10]. Now we know we should assign the third person and the fourth person to city B.

  3. We can solve this problem by sorting based on the different cost between cityA and cityB. From the problem’s example, after sorting, we have [[30, 200], [10, 20], [30, 20], [400, 50]]. Now, we can calculate the total cost. The first half people go to city A, the second half people go to city B.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func twoCitySchedCost(costs [][]int) int {
    res := 0
    sort.Slice(costs, func(i, j int) bool {
        return (costs[i][0] - costs[i][1]) < (costs[j][0] - costs[j][1])
    })

    for _, cost := range costs[:len(costs)/2] {
        res += cost[0]
    }
    for _, cost := range costs[len(costs)/2:] {
        res += cost[1]
    }

    return res
}

Explanation 2

  1. We can also use Dynamic Programming to solve this problem.

  2. Dynamic init is dp[i][j] represetns the total cost for i + j people such that i people go to city A, and j people go to city B. The length of the dp array is dp[len(costs)/2+1][len(costs)/ 2 + 1].

  3. Dynamic base is dp[0][0] = 0 since if no people go to city A and no people go to city B, then the total cost will be 0. For the left most column, dp[i][0], if no people go to city B, then the total cost dp[i][0] = costs[i-1][0] + dp[i-1][0];. For the top row, if no people go to city A, then the total cost dp[0][j] = costs[i-1][1] + dp[0][i-1];.

  4. Dynamic function is for the index i + j -1 person, if he/she goes to city A, then the total cost will be costs[r + c - 1][0] + dp[r-1][c];. If he/she goes to city B, then the total cost will be costs[r + c - 1][1] + dp[r][c-1];. So, dp[r][c] will take the minimum between these two values.

  5. Dynamic result is dp[len(costs)/2+1][len(costs)/ 2 + 1] which represents the total cost for half people go to city A and half people go to city B.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func twoCitySchedCost(costs [][]int) int {
    n := len(costs) / 2
    dp := make([][]int, n + 1)
    for i := range dp {
        dp[i] = make([]int, n + 1)
    }

    for r := 1; r <= n; r++ {
        dp[r][0] = costs[r-1][0] + dp[r-1][0]
    }
    for c := 1; c <= n; c++ {
        dp[0][c] = costs[c-1][1] + dp[0][c-1]
    }

    for r := 1; r <= n; r++ {
        for c := 1; c <= n; c++ {
            cityACost := costs[r + c - 1][0] + dp[r-1][c]
            cityBCost := costs[r + c - 1][1] + dp[r][c-1]
            dp[r][c] = min(cityACost, cityBCost)
        }
    }

    return dp[n][n]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Reverse String

Write a function that reverses a string. The input string is given as an array of characters char[].

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

You may assume all the characters consist of printable ascii characters.

Example 1:

1
2
Input: ["h","e","l","l","o"]
Output: ["o","l","l","e","h"]

Example 2:

1
2
Input: ["H","a","n","n","a","h"]
Output: ["h","a","n","n","a","H"]

Hint 1:

The entire logic for reversing a string is based on using the opposite directional two-pointer approach!

Explanation

  1. We can loop the string from beginning to the middle. Swap it with character at index s.length-1-i.

Solution

1
2
3
4
5
func reverseString(s []byte)  {
    for i := 0; i < len(s) / 2; i++ {
        s[i], s[len(s) - 1 - i] = s[len(s) - 1 - i], s[i]
    }
}

Random Pick with Weight

Given an array w of positive integers, where w[i] describes the weight of index i, write a function pickIndex which randomly picks an index in proportion to its weight.

Note:

  1. 1 <= w.length <= 10000

  2. 1 <= w[i] <= 10^5

  3. pickIndex will be called at most 10000 times.

Example 1:

1
2
3
4
Input:
["Solution","pickIndex"]
[[[1]],[]]
Output: [null,0]

Example 2:

1
2
3
4
Input:
["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
[[[1,3]],[],[],[],[],[]]
Output: [null,0,1,1,1,0]

Explanation of Input Syntax:

The input is two lists: the subroutines called and their arguments. Solution’s constructor has one argument, the array w. pickIndex has no arguments. Arguments are always wrapped with a list, even if there aren’t any.

Explanation

  1. This problem asks us to random pick a number based on their weight. For example, if the input array is [1, 3], then we pick 1 in probability 1/4, pick 3 in probability 3/4. Since random() will generate an equal probability number, instead of generate using rand() % 2, we will randomly generate using rand() % 4. If the random number is 0, then we pick 1, if the random number is from 1 to 3 inclusive, then we pick 3.

  2. We will generate an accumulate sum array first. If the input is [1, 3, 2], then the accumulate sum array will be [1, 4, 6]. The sum of all number is 6, so we will generate a random number by n = rand() % 6 + 1, which is in between 1 to 6 inclusive. If the random number is 1, we return index 0; if the random number is either 2, 3, 4, we return index 1. If the random number is either 5, 6, we return index 2. In other words, we will pick the first number from the accumulate sum array that is greater than or equal than the random number, and that number’s index is the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
type Solution struct {
    AccuSum []int
    Sum int
}


func Constructor(w []int) Solution {
    accuSum := make([]int, len(w))
    sum := 0
    for i, n := range w {
        sum += n
        accuSum[i] = sum
    }
    return Solution{accuSum, sum}
}


func (this *Solution) PickIndex() int {
    n := rand.Intn(this.Sum) + 1
    return this.BinarySearch(n)
}

func (this Solution) BinarySearch(n int) int {
    left := 0
    right := len(this.AccuSum) - 1
    for left < right {
        mid := left + (right - left) / 2
        if this.AccuSum[mid] < n {
            left = mid + 1
        } else {
            right = mid
        }
    }
    return left
}


/**
 * Your Solution object will be instantiated and called as such:
 * obj := Constructor(w);
 * param_1 := obj.PickIndex();
 */

Queue Reconstruction by Height

Suppose you have a random list of people standing in a queue. Each person is described by a pair of integers (h, k), where h is the height of the person and k is the number of people in front of this person who have a height greater than or equal to h. Write an algorithm to reconstruct the queue.

Note:

The number of people is less than 1,100.

Example

1
2
3
4
5
Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

Hint 1:

What can you say about the position of the shortest person? If the position of the shortest person is i, how many people would be in front of the shortest person?

Hint 2:

Once you fix the position of the shortest person, what can you say about the position of the second shortest person?

Explanation

  1. First, we sort the input array by the higher height h in front, if same height, then small k in front.

  2. After we sort the array, we can create a result list. Iterate the sorted array, we add each iterated sub array to the result list on position equals to the the sub array’s k value.

  3. For example, if input is [[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]. After sort, we have [[7,0], [7,1], [6,1], [5,0], [5,2], [4,4]]. Each iteration will be:

1
2
3
4
5
6
		[[7,0]]
		[[7,0], [7,1]]
		[[7,0], [6,1], [7,1]]
		[[5,0], [7,0], [6,1], [7,1]]
		[[5,0], [7,0], [5,2], [6,1], [7,1]]
		[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
  1. At the end, we convert the result list to array and return it.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func reconstructQueue(people [][]int) [][]int {
    res := make([][]int, len(people))
    sort.Slice(people, func(i, j int) bool {
        if people[i][0] == people[j][0] {
            return people[i][1] < people[j][1]
        } else {
            return people[i][0] > people[j][0]
        }
    })

    for i, p := range people {
        if res[p[1]] == nil {
            res[i] = p
        } else {
            copy(res[(p[1] + 1):], res[p[1]:])
            res[p[1]] = p
        }
    }

    return res
}

Coin Change 2

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.

Example 1:

1
2
3
4
5
6
7
Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

Example 2:

1
2
3
Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

1
2
Input: amount = 10, coins = [10]
Output: 1

Note:

You can assume that

  • 0 <= amount <= 5000

  • 1 <= coin <= 5000

  • the number of coins is less than 500

  • the answer is guaranteed to fit into signed 32-bit integer

Explanation 1

  1. We can use dynamic programming to solve this problem. Dynamic state is dp[coins.length][amount+1]. In this two dimensional array, dp[i][j] means the total ways of making up amount j using the first i index coins.

  2. Dynamic init is dp[i][0] = 1 for any i because if the amount is 0, then we have only 1 way of making up amount 0, which is []. Also, if we only have 1 coin, then dp[0][i] = 0 + dp[0][i - coins[0]] because if we exclude this coin, then we have 0 way to make the amount i, and if we include this coin, then we have the same number of choices as dp[0][i - coins[0].

  3. Dynamic function. If coins[i] > curAmount, we must exclude this coin, then dp[i][a] = dp[i-1][a] because we cannot use the current coins because it’s too large. Else dp[i][a] = dp[i-1][a] + dp[i][a - coins[i] because now the total ways is the total ways of exclude the current coint plus include the current coins with updating amount.

  4. Dynamic result is dp[coins.length-1][amount], which uses all coins and make up amount amount.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func change(amount int, coins []int) int {
    if amount == 0 { return 1 }
    if len(coins) == 0 { return 0 }

    dp := make([][]int, len(coins))
    for i := range dp {
        dp[i] = make([]int, amount+1)
    }

    for i := 0; i < len(dp); i++ {
        dp[i][0] = 1
    }
    for i := 1; i < len(dp[0]); i++ {
        if coins[0] <= i {
            dp[0][i] = dp[0][i - coins[0]]
        }
    }

    for r := 1; r < len(dp); r++ {
        for c := 0; c < len(dp[0]); c++ {
            if coins[r] > c {
                dp[r][c] = dp[r-1][c]
            } else {
                dp[r][c] = dp[r-1][c] + dp[r][c-coins[r]]
            }
        }
    }

    return dp[len(coins)-1][amount]
}

Explanation 2

  1. We can save space by using only 1 dimensional array.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func change(amount int, coins []int) int {
    if amount == 0 { return 1 }
    if len(coins) == 0 { return 0 }

    dp := make([]int, amount+1)
    dp[0] = 1

    for r := 0; r < len(coins); r++ {
        for c := 0; c < len(dp); c++ {
            if coins[r] <= c {
                dp[c] += dp[c-coins[r]]
            }
        }
    }

    return dp[amount]
}

Explanation 3

  1. We can also use top down approach to solve this problem.

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func change(amount int, coins []int) int {
    if amount == 0 { return 1}
    if len(coins) == 0 { return 0 }

    dp := make([][]int, len(coins))
    for i := range dp {
        for j := 0; j <= amount; j++ {
            dp[i] = append(dp[i], -1)
        }
    }

    return helper(amount, coins, 0, 0, dp)
}

func helper(amount int, coins []int, curIdx int, sum int, dp[][] int) int {
    if sum == amount { return 1 }
    if sum > amount { return 0 }
    if dp[curIdx][sum] != -1 { return dp[curIdx][sum] }

    res := 0
    for i := curIdx; i < len(coins); i++ {
        res += helper(amount, coins, i, sum+coins[i], dp)
    }
    dp[curIdx][sum] = res

    return res
}

Week 2: June 8th–June 14th

Power of Two

Given an integer, write a function to determine if it is a power of two.

Example 1:

1
2
3
Input: 1
Output: true
Explanation: 20 = 1

Example 2:

1
2
3
Input: 16
Output: true
Explanation: 24 = 16

Example 3:

1
2
Input: 218
Output: false

Explanation

  1. We can use bit manipulation to solve this problem. We notice that every number that is power of two will have a binary pattern that the only highest bit is 1, every other bit is 0. For example:

    1
    2
    3
    4
    5
     1 -> 1
 2 -> 10
 4 -> 100
 8 -> 1000
 16 -> 10000

  2. We can check from the lowest bit to the highest bit, count how many 1 does this number has by using AND operator with 1 and the current bit, update the counter, then move the number n to right by 1 bit.

  3. At the end we check if counter equals 1.

Solution

1
2
3
func isPowerOfTwo(n int) bool {
    return n > 0 && (n & (n - 1)) == 0
}

Is Subsequence

Given a string s and a string t, check if s is subsequence of t.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ace" is a subsequence of "abcde" while "aec" is not).

Follow up:

If there are lots of incoming S, say S1, S2, … , Sk where k >= 1B, and you want to check one by one to see if T has its subsequence. In this scenario, how would you change your code?

Credits:

Special thanks to @pbrother for adding this problem and creating all test cases.

Example 1:

1
2
Input: s = "abc", t = "ahbgdc"
Output: true

Example 2:

1
2
Input: s = "axc", t = "ahbgdc"
Output: false

Constraints:

  • 0 <= s.length <= 100

  • 0 <= t.length <= 10^4

  • Both strings consists only of lowercase characters.

Explanation 1

  1. We can use recursive approach to solve this problem. Compare the first string of both strings, if they are equal, then we recursively call the main function with s[1:] and t[1:]. Else, we recursively call the main function with s and t[1:].

Solution 1

1
2
3
4
5
6
7
8
9
func isSubsequence(s string, t string) bool {
    if len(s) == 0 { return true }
    if len(t) == 0 { return false }
    if s[0] == t[0] {
        return isSubsequence(s[1:], t[1:])
    } else {
        return isSubsequence(s, t[1:])
    }
}

Explanation 2

  1. We can use two pointers approach to solve this problem. We use variable sIdx points to the current character at string s, and use i points to the current character at string t. Then, loop through all characters in t. If s[sIdx] is equal to t[i], then we increase sIdx. If sIdx is equals to length of s, then we immediately return true. Outside the loop, we return false.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func isSubsequence(s string, t string) bool {
    if len(s) == 0 { return true }
    if len(t) == 0 { return false }
    sIdx := 0
    for i := 0; i < len(t); i++ {
        if s[sIdx] == t[i] {
            sIdx += 1
        }
        if sIdx == len(s) {
            return true
        }
    }
    return false
}

Explanation 3

  1. For the follow up question, if we have a lot of s, and t is unchanged, how can we improve. We can start working for t since it’s unchanged. First, we can create an array of list List[26]; in other words, for each character, it has a list that contains all this character’s index at t. Since we are loop through t from left to right, then each array element’s list’s index will be sorted.

  2. Next, we loop through s. For each character, we check if its corresponding list is empty or not, if empty, that means there’s no current s’s character in t, so we return false. Else, we use binary search in the corresponding character’s list to search for the insertion index for startTIdx. startTIdx is initialized to 0, and it is the index of t that we are begin to search. Now if the binary search result insertion is equals to its corresponding list’s size, that means startTIdx is greater than the last index of the current character that we can find in t, so we return false. Else, we updated startTIdx be insertion plus one.

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
func isSubsequence(s string, t string) bool {
    if len(s) == 0 { return true }
    if len(t) == 0 { return false }

    arr := make([][]int, 26)
    for i, tChar := range t {
        curIdx := tChar - 'a'
        arr[curIdx] = append(arr[curIdx], i)
    }

    startTIdx := 0
    for _, sChar := range s {
        curIdx := sChar - 'a'
        if len(arr[curIdx]) == 0 { return false }
        insertion := binarySearch(arr[curIdx], startTIdx)
        if insertion == len(arr[curIdx]) { return false }
        startTIdx = arr[curIdx][insertion] + 1
    }

    return true
}

func binarySearch(lst []int, target int) int {
    left, right := 0, len(lst) - 1
    for left < right {
        mid := left + (right - left) / 2
        if target > lst[mid] {
            left = mid + 1
        } else {
            right = mid
        }
    }

    if target <= lst[left] {
        return left
    } else {
        return left + 1
    }
}

Search Insert Position

Given a sorted array and a target value, return the index if the target is found. If not, return the index where it would be if it were inserted in order.

You may assume no duplicates in the array.

Example 1:

1
2
Input: [1,3,5,6], 5
Output: 2

Example 2:

1
2
Input: [1,3,5,6], 2
Output: 1

Example 3:

1
2
Input: [1,3,5,6], 7
Output: 4

Example 4:

1
2
Input: [1,3,5,6], 0
Output: 0

Explanation

  1. We can use binary search to solve this problem.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func searchInsert(nums []int, target int) int {
    left, right := 0, len(nums) - 1
    for left < right {
        mid := left + (right - left) / 2
        if target > nums[mid] {
            left = mid + 1
        } else {
            right = mid
        }
    }
    if target <= nums[left] {
        return left
    } else {
        return left + 1
    }
}

Sort Colors

Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note: You are not suppose to use the library’s sort function for this problem.

Example:

1
2
Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

Follow up:

  • A rather straight forward solution is a two-pass algorithm using counting sort. First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.

  • Could you come up with a one-pass algorithm using only constant space?

Explanation

  1. We can use two pointer method to solve this problem. First, we delcare a redPointer points at the beginning, and a bluePointer points at the end index. Now, iterate from the beginning, if the element is red (0), then we swap it with the element that redPointer points at, redPointer moving forward. If the element is blue (2), then we swap it with the element that the bluePointer points at, bluePointer moving backward.

  2. One corner case is when the element that the blue pointer points at is red (0), when iterating, if the current iterated element is blue (2), then we swap it with the red (0), now the iterator shouldn’t move to the next, it should check this iterated current element again and move the red (0) element to the correct position.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func sortColors(nums []int)  {
    cur, p0, p2 := 0, 0, len(nums) - 1
    for cur <= p2 {
        if nums[cur] == 0 {
            nums[cur], nums[p0] = nums[p0], nums[cur]
            p0 += 1
            cur += 1
        } else if nums[cur] == 2 {
            nums[cur], nums[p2] = nums[p2], nums[cur]
            p2 -= 1
        } else {
            cur += 1
        }
    }
}

Insert Delete GetRandom O(1)

Design a data structure that supports all following operations in average O(1) time.

  • insert(val): Inserts an item val to the set if not already present.

  • remove(val): Removes an item val from the set if present.

  • getRandom: Returns a random element from current set of elements. Each element must have the same probability of being returned.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// Init an empty set.
RandomizedSet randomSet = new RandomizedSet();

// Inserts 1 to the set. Returns true as 1 was inserted successfully.
randomSet.insert(1);

// Returns false as 2 does not exist in the set.
randomSet.remove(2);

// Inserts 2 to the set, returns true. Set now contains [1,2].
randomSet.insert(2);

// getRandom should return either 1 or 2 randomly.
randomSet.getRandom();

// Removes 1 from the set, returns true. Set now contains [2].
randomSet.remove(1);

// 2 was already in the set, so return false.
randomSet.insert(2);

// Since 2 is the only number in the set, getRandom always return 2.
randomSet.getRandom();

Explanation

  1. If we don’t consider the $O(1)$ runtime, we can easily use a set to solve this problem, but now the required runtime is $O(1)$, we know that to get a specific index element in a set is not $O(1)$, so we cannot use a set to solve this problem. To solve this, we need to use an ArrayList lst and a HashMap hm with hashmap key is the inserted value, hashmap value is the ArrayList’s index.

  2. For the Insert(val) method, if the hashmap already contains the value, we return false immdediately. Else, we can just push the val to the end of the ArrayList lst and return true.

  3. For the remove(val) method, if the hashmap doesn’t contain the value, we return false immediately. Else, we get the index pos of the removed value, and update this position in the array listlst[pos] with the last array list’s element. For example, if the array list is [2, 5, 7, 9] and we want to remove 5, then after update, we have [2, 9, 7, 9], we also update the hashmap[lastEle] = pos. Next, we want to remove the last element in the array list, and remove hashmap[val].

  4. For the getRandom method, we can just return arraylist’s random index value.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
type RandomizedSet struct {
    Lst []int
    Hm map[int]int
}


/** Initialize your data structure here. */
func Constructor() RandomizedSet {
    lst := make([]int, 0)
    hm := make(map[int]int)

    return RandomizedSet{lst, hm}
}


/** Inserts a value to the set. Returns true if the set did not already contain the specified element. */
func (this *RandomizedSet) Insert(val int) bool {
    if _, ok := this.Hm[val]; ok { return false }
    this.Lst = append(this.Lst, val)
    this.Hm[val] = len(this.Lst) - 1
    return true
}


/** Removes a value from the set. Returns true if the set contained the specified element. */
func (this *RandomizedSet) Remove(val int) bool {
    if _, ok := this.Hm[val]; !ok { return false }
    pos := this.Hm[val]
    lastEle := this.Lst[len(this.Lst) - 1]
    this.Lst[pos] = lastEle
    this.Hm[lastEle] = pos
    this.Lst = this.Lst[:len(this.Lst)-1]
    delete(this.Hm, val)
    return true
}


/** Get a random element from the set. */
func (this *RandomizedSet) GetRandom() int {
    return this.Lst[rand.Intn(len(this.Lst))]
}


/**
 * Your RandomizedSet object will be instantiated and called as such:
 * obj := Constructor();
 * param_1 := obj.Insert(val);
 * param_2 := obj.Remove(val);
 * param_3 := obj.GetRandom();
 */

Largest Divisible Subset

Given a set of distinct positive integers, find the largest subset such that every pair (Si, Sj) of elements in this subset satisfies:

Si % Sj = 0 or Sj % Si = 0.

If there are multiple solutions, return any subset is fine.

Example 1:

1
2
Input: [1,2,3]
Output: [1,2] (of course, [1,3] will also be ok)

Example 2:

1
2
Input: [1,2,4,8]
Output: [1,2,4,8]

Explanation

  1. Since the small number cannot be divisible by the large number, we need to first sort the array.

  2. We can use Dynamic Programming to solve this problem. dp[i] means the maximum number of divisible elements from index 0 to index i inclusive.

  3. Dynamic init is all dp[i] equals 1 since nums[i] themselves is one number.

  4. Next, we loop i from 0 to the last index, inside the for loop, we create another for loop that loops from i-1 to 0. If nums[i] % nums[j] == 0 and dp[j]+1 > dp[i], then we update dp[i], and we record nums[j] can divisible nums[i] by having an array divisibleInd[i] to record the index of the number that can divisible divisible[i], in this case, divisibleInd[i] = j. Outside of the inner for loop, we have the maximum length of divisible number from index 0 to index i inclusive, then we update max = dp[i] and maxInd = i.

  5. Outside of these two for loops, now we have max that represents the maximum length of divisible numbers, in other words, the length of result array. We can get these elements by using the divisibleInd[] since it records each number’s divisible number’s index. For example, if the input array is [2, 4, 6, 8], then 4 is pointing to 2, 6 is pointing to 4, 8 is pointing to 6.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func largestDivisibleSubset(nums []int) []int {
    res := make([]int, 0)
    if len(nums) == 0 { return res }
    sort.Ints(nums)

    dp := make([]int, len(nums))
    divisibleInd := make([]int, len(nums))

    for i := range dp {
        dp[i] = 1
        divisibleInd[i] = -1
    }

    max := 0
    maxInd := -1

    for i := 0; i < len(nums); i++ {
        for j := i-1; j >= 0; j-- {
            if nums[i] % nums[j] == 0 && dp[j] + 1 > dp[i] {
                dp[i] = dp[j] + 1
                divisibleInd[i] = j
            }
        }

        if dp[i] > max {
            max = dp[i]
            maxInd = i
        }
    }

    for maxInd != -1 {
        res = append(res, nums[maxInd])
        maxInd = divisibleInd[maxInd]
    }

    return res
}

Cheapest Flights Within K Stops

There are n cities connected by m flights. Each flight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Example 1:

Input:

n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]

src = 0, dst = 2, k = 1

Output: 200

Explanation:

The graph looks like this:

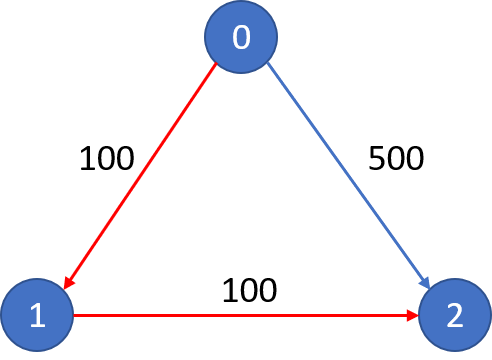
Cheapest Flights Within K Stops

The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:

Input:

n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]

src = 0, dst = 2, k = 0

Output: 500

Explanation:

The graph looks like this:

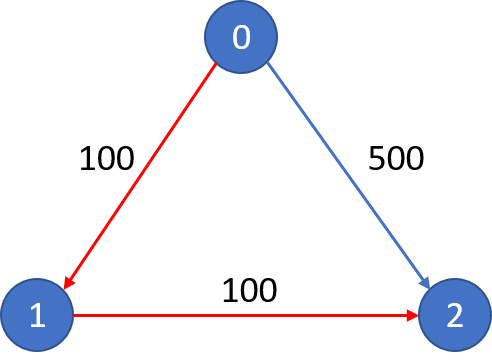
Cheapest Flights Within K Stops

The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Constraints:

  • The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.

  • The size of flights will be in range [0, n * (n - 1) / 2].

  • The format of each flight will be (src, dst, price).

  • The price of each flight will be in the range [1, 10000].

  • k is in the range of [0, n - 1].

  • There will not be any duplicated flights or self cycles.

Explanation

  1. Similar to Dijkstra’s Algorithm, but in this problem we are limited to K+1 edges from the source to destination.

  2. First, we build the adjacent list. For each neighbor element, besides the destination vertex, we also keep track of the distance to reach the destination. For example, from the problem’s example 1, we have adjacent list [[{1, 100}, {2, 500}], [{2, 100}], []].

  3. In Dijkstra’s Algorithm, we start from the source vertex, in other word, we start from the smallest distance from the source. In this problem, we can create a priority queue, each element in the priority queue will be an array of size 3; the first array element is the vertex, the second array element is the distance from source, the third element is the number of edges from source to this vertex. So initially, we push int[]{src, 0, 0} to the priority queue.

  4. While the priority queue is not empty, we poll the array [vertex, distance, numEdge] from the queue. If this array’s vertex is the destination, then we immediately return its distance. If this array’s numEdge is equal to K + 1, we skip this vertex since we can’t have more than K stops or K + 1 edges from the source. Else, we loop through the neighbors of the current array’s vertex. For each neighbor, we update its distance be distance + neighbor[1], update its number of edge be numEdge + 1, and store them to the priority queue. Repeat until the priority queue is empty.

  5. If the priority queue is empty and we still not found the destination, then we return -1.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
func findCheapestPrice(n int, flights [][]int, src int, dst int, K int) int {
    adjLst := make([][]Pair, n)
    for _, flight := range flights {
        adjLst[flight[0]] = append(adjLst[flight[0]], Pair{flight[1], flight[2]})
    }
    pq := &minHeap{}
    heap.Init(pq)

    heap.Push(pq, []int{src, 0, 0})
    for pq.Len() > 0 {
        cur := heap.Pop(pq).([]int)
        vertex := cur[0]
        distance := cur[1]
        numEdge := cur[2]
        if vertex == dst { return distance }
        if numEdge == K + 1 { continue }
        for _, neighbor := range adjLst[vertex] {
            heap.Push(pq, []int{neighbor[0], distance + neighbor[1], numEdge+1})
        }
    }
    return -1
}

type Pair []int

type minHeap [][]int

func (h minHeap) Len() int {
    return len(h)
}

func (h minHeap) Less(i, j int) bool {
    return h[i][1] < h[j][1]
}

func (h minHeap) Swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h *minHeap) Push(x interface{}) {
    *h = append(*h, x.([]int))
}

func (h *minHeap) Pop() interface{} {
    old := *h
    item := old[len(old)-1]
    *h = old[:len(old)-1]
    return item
}

Week 3: June 15th–June 21st

Search in a Binary Search Tree

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST that the node’s value equals the given value. Return the subtree rooted with that node. If such node doesn’t exist, you should return NULL.

For example,

1
2
3
4
5
6
7
8
Given the tree:
        4
       / \
      2   7
     / \
    1   3

And the value to search: 2

You should return this subtree:

1
2
3
      2
     / \
    1   3

In the example above, if we want to search the value 5, since there is no node with value 5, we should return NULL.

Note that an empty tree is represented by NULL, therefore you would see the expected output (serialized tree format) as [], not null.

Explanation 1

  1. Since the tree is a binary search tree, so the left child value is less than the root value, and the right child value is greater than the root value.

  2. We can do it in a recursive way. If root is NULL, then we return NULL. If root value is equal to target value, then we return the root. If target value is less than the root value, then we recursively call the main function with root.left and the target value. Else, we recursively call the main function with root.right and the target value.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func searchBST(root *TreeNode, val int) *TreeNode {
    if root == nil { return nil }
    if val == root.Val { return root }
    if val < root.Val { return searchBST(root.Left, val) }
    return searchBST(root.Right, val)
}

Explanation 2

  1. We can also do it in iterative way. First, we create a pointer cur pointing to the root. While cur is not NULL, then we check if cur.val is equal to target, then we return cur. Else if target value is less than cur.val, then we update cur = cur.left. Else if target value is greater than cur.val, we update cur = cur.right. Outside the while loop, that means cur is NULL and we haven’t found the target value, so we return NULL.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func searchBST(root *TreeNode, val int) *TreeNode {
    if root == nil { return nil }
    cur := root
    for cur != nil {
        if val == cur.Val { return cur }
        if val < cur.Val {
            cur = cur.Left
        } else { cur = cur.Right }
    }
    return nil
}

Validate IP Address

Write a function to check whether an input string is a valid IPv4 address or IPv6 address or neither.

IPv4 addresses are canonically represented in dot-decimal notation, which consists of four decimal numbers, each ranging from 0 to 255, separated by dots (“.”), e.g.,172.16.254.1;

Besides, leading zeros in the IPv4 is invalid. For example, the address 172.16.254.01 is invalid.

IPv6 addresses are represented as eight groups of four hexadecimal digits, each group representing 16 bits. The groups are separated by colons (“:”). For example, the address 2001:0db8:85a3:0000:0000:8a2e:0370:7334 is a valid one. Also, we could omit some leading zeros among four hexadecimal digits and some low-case characters in the address to upper-case ones, so 2001:db8:85a3:0:0:8A2E:0370:7334 is also a valid IPv6 address(Omit leading zeros and using upper cases).

However, we don’t replace a consecutive group of zero value with a single empty group using two consecutive colons (::) to pursue simplicity. For example, 2001:0db8:85a3::8A2E:0370:7334 is an invalid IPv6 address.

Besides, extra leading zeros in the IPv6 is also invalid. For example, the address 02001:0db8:85a3:0000:0000:8a2e:0370:7334 is invalid.

Note: You may assume there is no extra space or special characters in the input string.

Example 1:

1
2
3
4
5
Input: "172.16.254.1"

Output: "IPv4"

Explanation: This is a valid IPv4 address, return "IPv4".

Example 2:

1
2
3
4
5
Input: "2001:0db8:85a3:0:0:8A2E:0370:7334"

Output: "IPv6"

Explanation: This is a valid IPv6 address, return "IPv6".

Example 3:

1
2
3
4
5
Input: "256.256.256.256"

Output: "Neither"

Explanation: This is neither a IPv4 address nor a IPv6 address.

Explanation

  1. If the input string has . that means we need to check if it’s IPv4. Else if the string has :, that means we need to check if it’s IPv6. If the input string doesn’t have neither . nor :, then we return Neither.

  2. When we check if the input string is IPv4. First, we split the string by . and check the length of the splitted array. If the length is not 4, then we immediately return Neither. Next, we loop through and check these 4 string tokens. If the token’s length is 0 or greater than 3, then we immediately return Neither. Next, we check if the first character of the token string is 0 and its length is not 1, then we return Neither immediately. Next, we check if this token string can be converted into integer and its value is between 0 and 255. If one of the condition is false, we return Neither. After checking these 4 token strings, we return IPv4.

  3. When we check if the input string is IPv6. First, we split the string by : and check the length of the splitted array. If the length is not 8, then we immediately return Neither. Next, we loop through and check these 8 string tokens. If the token’s length is 0 or greater than 4, then we immediately return Neither. Next, we loop through every character of the token and see if every character is in the range of [0-9a-fA-F]. If one of the condition is false, we return Neither. After checking these 8 token strings, we return IPv6.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func validIPAddress(IP string) string {
    if strings.Index(IP, ".") > -1 {
        return checkIPv4(IP)
    } else if strings.Index(IP, ":") > -1 {
        return checkIPv6(IP)
    } else {
        return "Neither"
    }
}

func checkIPv4(IP string) string {
    tokens := strings.Split(IP, ".")
    if len(tokens) != 4 { return "Neither" }
    for _, token := range tokens {
        if len(token) == 0 || len(token) > 3 { return "Neither" }
        if token[0] == '0' && len(token) != 1 || token[0] == '-' { return "Neither" }
        num, err := strconv.Atoi(token)
        if err != nil || num > 255 || num < 0 { return "Neither" }
    }
    return "IPv4"
}

func checkIPv6(IP string) string {
    tokens := strings.Split(IP, ":")
    if len(tokens) != 8 { return "Neither" }
    for _, token := range tokens {
        if len(token) == 0 || len(token) > 4 { return "Neither" }
        for _, ch := range token {
            if !(ch >= '0' && ch <= '9' || ch >= 'a' && ch <= 'f' || ch >= 'A' && ch <= 'F') {
                return "Neither"
            }
        }
    }
    return "IPv6"
}

Surrounded Regions

Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example:

1
2
3
4
X X X X
X O O X
X X O X
X O X X

After running your function, the board should be:

1
2
3
4
X X X X
X X X X
X X X X
X O X X

Explanation:

Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Explanation

  1. First, we can find the boarder’s character, if they are ‘O’, then we flood fill them to ‘Y’.

  2. Next, we can replace the rest of ‘O’ to be ‘X’ since they are not connected to the boarder.

  3. Finally, replace all ‘Y’ back to ‘O’.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func solve(board [][]byte)  {
    row := len(board)
    if row <= 2 { return }
    col := len(board[0])
    if col <= 2 { return }

    for r := 0; r < row; r++ {
        floodFill(board, r, 0)
        floodFill(board, r, col-1)
    }
    for c := 0; c < col; c++ {
        floodFill(board, 0, c)
        floodFill(board, row-1, c)
    }

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if board[r][c] == 'Y' {
                board[r][c] = 'O'
            } else if board[r][c] == 'O' {
                board[r][c] = 'X'
            }
        }
    }
}

func floodFill(board [][]byte, r, c int) {
    if r < 0 || r >= len(board) || c < 0 || c >= len(board[0]) { return }
    if board[r][c] == 'X' || board[r][c] == 'Y' { return }
    board[r][c] = 'Y'
    floodFill(board, r-1, c)
    floodFill(board, r+1, c)
    floodFill(board, r, c-1)
    floodFill(board, r, c+1)
}

H-Index II

Given an array of citations sorted in ascending order (each citation is a non-negative integer) of a researcher, write a function to compute the researcher’s h-index.

According to the definition of h-index on Wikipedia: “A scientist has index h if h of his/her N papers have at least h citations each, and the other N − h papers have no more than h citations each.”

Example:

1
2
3
4
5
6
Input: citations = [0,1,3,5,6]
Output: 3
Explanation: [0,1,3,5,6] means the researcher has 5 papers in total and each of them had
             received 0, 1, 3, 5, 6 citations respectively.
             Since the researcher has 3 papers with at least 3 citations each and the remaining
             two with no more than 3 citations each, her h-index is 3.

Note:

If there are several possible values for h, the maximum one is taken as the h-index.

Follow up:

  • This is a follow up problem to H-Index, where citations is now guaranteed to be sorted in ascending order.

  • Could you solve it in logarithmic time complexity?

Hint 1:

Expected runtime complexity is in O(log n) and the input is sorted.

Explanation

  1. If we want to solve it in $O(\log n)$ time, we can use binary search method. While left < righ, when we get the mid index, then we calculate how many elements is equal to or greater than citations[mid] by len - mid. Assume len-mid is the h, we compare it with citations[mid] since h paper should have at least h citations each.

  2. If citations[mid] is less than len-mid, that means h should be smaller, so we update left = mid + 1.

  3. If citations[mid] is greater than len-mid, that means h should be bigger, so we update right = mid.

  4. Outside the while loop, len-left will be the h.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func hIndex(citations []int) int {
    n := len(citations)
    if n == 0 || citations[n-1] == 0 { return 0 }

    left, right := 0, n - 1

    for left < right {
        mid := left + (right - left) / 2
        count := n - mid
        if citations[mid] < count {
            left = mid + 1
        } else {
            right = mid
        }
    }

    return n - left
}

Longest Duplicate Substring

Given a string S, consider all duplicated substrings: (contiguous) substrings of S that occur 2 or more times. (The occurrences may overlap.)

Return any duplicated substring that has the longest possible length. (If S does not have a duplicated substring, the answer is "".)

Example 1:

1
2
Input: "banana"
Output: "ana"

Example 2:

1
2
Input: "abcd"
Output: ""

Note:

  1. 2 <= S.length <= 10^5

  2. S consists of lowercase English letters.

Hint 1:

Binary search for the length of the answer. (If there’s an answer of length 10, then there are answers of length 9, 8, 7, …)

Hint 2:

To check whether an answer of length K exists, we can use Rabin-Karp ‘s algorithm.

Explanation

  1. Assume the longest duplicate substring has length ldsLen, we create a helper function to find the longest duplicate substring with length ldsLen from the input string. If we find it, then we update the result string equal to the longest duplicate substring we found; and we increase ldsLen and run it with helper function. Else we don’t find it, we can decrease ldsLen and run it with the helper function. We can use binary search to find the largest ldsLen.

  2. In the helper function, we can loop the startIdx from index 0 to index len(S) - ldsLen + 1 inclusive. In each iteration, we check if the current string S[startIdx, startIdx + ldsLen] is in the set or no. If it’s not in the set, we add it to the set. Else, that means we find a dupliate string S[startIdx, startIdx + ldsLen] with length ldsLen.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
func longestDupSubstring(S string) string {
    res := ""
    left, right := 0, len(S) - 1

    for left <= right {
        mid := left + (right - left) / 2
        lds := helper(S, mid)
        if (lds != "") {
            res = lds
            left = mid + 1
        } else {
            right = mid - 1
        }
    }

    return res
}

func helper(S string, ldsLen int) string {
    if ldsLen == 0 { return "" }
    set := make(map[string]bool)

    for i := 0; i < len(S) - ldsLen + 1; i++ {
        curStr := S[i:i+ldsLen]
        if _, ok := set[curStr]; ok {
            return curStr
        } else {
            set[curStr] = true
        }
    }

    return ""
}

Permutation Sequence

The set [1,2,3,...,n] contains a total of n! unique permutations.

By listing and labeling all of the permutations in order, we get the following sequence for n = 3:

  1. "123"

  2. "132"

  3. "213"

  4. "231"

  5. "312"

  6. "321"

Given n and k, return the kth permutation sequence.

Note:

  • Given n will be between 1 and 9 inclusive.

  • Given k will be between 1 and n! inclusive.

Example 1:

1
2
Input: n = 3, k = 3
Output: "213"

Example 2:

1
2
Input: n = 4, k = 9
Output: "2314"

Explanation

  1. For example, when n=4, k=9:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
     1234
 1243
 1324
 1342
 1423
 1432
 2134
 2143
 2314  <= k = 9
 2341
 2413
 2431
 3124
 3142
 3214
 3241
 3412
 3421
 4123
 4132
 4213
 4231
 4312
 4321

  2. The most significant digit can be choosen from {1, 2, 3, 4}, and each number in the most significant digit is repeated (n-1)! = 6 times. So, in the result, the most significant digit will be the second (res[0] = 9 / 6 + 1 = 2) number, which is 2.

  3. Now we know the result’s most significant digit is the number 2, then we need to find out what’s the number for the second most significant digit, and we can only choose from number {1, 3, 4} in these 6 (3!) numbers: 2134, 2143, 2314, 2341, 2413, 2431. k is 9, now the new k' will become 9 % (3!) = 9 % 6 = 3. And each number {1, 3, 4} in the second most significant digit is repeated (n-2)! = 2 times. So, in the result, the second most significant digit will be the second (res[1] = 3 / 2 + 1 = 2) number, which is 3.

  4. Now we know the result is starting from 23, and we can only choose from number {1, 4} in these 2 (2!) numbers: 2314, 2341. k' is 3, now the new k'' will become 3 % (2!) = 3 % 2 = 1. And each number {1, 4} in the third most significant digit is appear (n-3)! = 1 time. So, in the result, the third most significant digit will be the first number, which is 1.

  5. Now we know the result is starting from 231, and there is only {4} left, so the last digit is 4, and the result will be 2314.

  6. Basically, after we find out the most significant digit by doing k / fac[i], then we need to find out the new k in the next most significant digit by doing k % fac[i], and repeat the process.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func getPermutation(n int, k int) string {
    factorial := make([]int, n)
    factorial[0] = 1
    for i := 1; i < n; i++ {
        factorial[i] = factorial[i-1] * i
    }

    num := make([]int, n)
    for i := 0; i < n; i++ {
        num[i] = i + 1
    }

    k -= 1 // start with index 0
    res := strings.Builder{}
    for i := n - 1; i >= 0; i-- {
        c := k / factorial[i]
        curDigit := strconv.Itoa(num[c])
        res.WriteString(curDigit)
        num = append(num[:c], num[c+1:]...)
        k = k % factorial[i]
    }

    return res.String()
}

Dungeon Game

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).

In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.

For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.

     
-2 (K) -3 3
-5 -10 1
10 30 -5 (P)

Note:

  • The knight’s health has no upper bound.

  • Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

Explanation

  1. We can use dynamic programming to solve this problem.

  2. Dynamic state is a two dimensional array. dp[r][c] means the initial health point before fighting at position (r, c), so the return result will be dp[0][0].

  3. Dynamic init, we create one more row and column, and we assign these whole new row and new column’s elements all be maximum number. We will start from the princess’s position, and the princess’s position depends on its down and right position. We will assign these two positions be 1 instead of maximum because after fighting at the pricness’s position, the knight at least have 1 health point before going to down or right position.

  4. Dynamic function, the health point before fighting is dp[r][c], so before fighting at its down position, the health point for dp[r+1][c] = dp[r][c] + dungeon[r][c], in other word, dp[r][c] is depend on its down position, so dp[r][c] = dp[r+1][c] - dungeon[r][c]. If the knight goes to the right position, then dp[r][c] = dp[r][c+1] - dungeon[r][c]. To use less point as possible, the knight will choose the less point to go to, so it is min[dp[r+1][c], dp[r][c+1]. If the subtraction result is negative, then we will lose, so dp[r][c] has at least 1 health point. Therefore, we get our dynamic function dp[r][c] = Math.max(1, Math.min(dp[r+1][c], dp[r][c+1]) - dungeon[r][c]).

  5. Dynamic result is dp[0][0] which is the beginning top left position.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func calculateMinimumHP(dungeon [][]int) int {
    row, col := len(dungeon) + 1, len(dungeon[0]) + 1
    dp := make([][]int, row)
    for i := range dp {
        dp[i] = make([]int, col)
    }

    for r := 0; r < len(dp); r++ {
        dp[r][col-1] = math.MaxInt32
    }
    for c := 0; c < len(dp[0]); c++ {
        dp[row-1][c] = math.MaxInt32
    }

    dp[row-1][col-2] = 1 // princess's down
    dp[row-2][col-1] = 1 // princess's right

    for r := row-2; r >= 0; r-- {
        for c := col-2; c >= 0; c-- {
            dp[r][c] = max(1, min(dp[r+1][c], dp[r][c+1])-dungeon[r][c])
        }
    }

    return dp[0][0]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Week 4: June 22nd–June 28th

Single Number II

Given a non-empty array of integers, every element appears three times except for one, which appears exactly once. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

1
2
Input: [2,2,3,2]
Output: 3

Example 2:

1
2
Input: [0,1,0,1,0,1,99]
Output: 99

Explanation 1

  1. If the input array is [10, 10, 13, 10], then the result should be 13. The binary representation of the input array would be:

    1
    2
    3
    4
     1010
 1010
 1101 <--- result
 1010

    For each bit, we sum every numbers’ value, then we get:

    1
     4131

    Then, we module each bit number by 3, then we get the result in binary:

    1
     1101

  2. We can code the above approach. Create an array bits[] of size 32. Loop i 32 times, for each bit bits[i], we inner loop the input array. For each number, to get its corresponding bit value, we can right shift the current number i times and AND 1. So we sum each number’s result to bits[i]. Also, each time, we take module 3 of bits[i].

  3. After we get the result bits[] in binary format, we can convert it back to integer. Loop 32 times, each time, we left shift the current bit i times and sum this result as our final result.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func singleNumber(nums []int) int {
    res := 0
    bits := make([]int, 32)

    for i := 0; i < 32; i++ {
        for _, num := range nums {
            bits[i] += num >> i & 1
            bits[i] %= 3
        }
    }

    for i := 0; i < 32; i++ {
        if i < 31 {
            res += bits[i] << i
        } else {
            res -= bits[i] << i
        }

    }

    return res
}

Explanation 2

  1. We can solve this problem in one pass. Now we create two variables int ones which records the number of same position bits have been occured 1 time, 4 time, 7 time… and int twos records the number of same position bits have been occured 2 time, 5 time, 8 time… . If the same position bits have been occured 3 time, 6 time, 9 time, then we think of them appear 0 time.

  2. Using this example input [10, 10, 13, 10] and loop through this array.

    • Current value in binary format: 1010; ones = [1010]; twos = [0000].
    • Current value in binary format: 1010; ones = [0000]; twos = [1010].
    • Current value in binary format: 1101; ones = [0101]; twos = [0010].
    • Current value in binary format: 1010; ones = [1101]; twos = [0000].

  3. We can calculate twos by twos = twos OR (ones AND num), and calculate ones by ones = ones XOR num. Now, if hit the first one, ones = 0 xor 1 = 1. If hit the second one, ones = 1 xor 1 = 0. If hit the third one, ones = 0 xor 1 = 1. Since we have seen three 1s, we want ones be 0. We can achieve this by also create a variable threes to record the number of bits have been occured three times. Then threes = ones & twos. Each iteration, after we calculate threes, we update ones = ones AND (NOT threes), similarlly for twos = twos AND (NOT threes).

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
func singleNumber(nums []int) int {
    ones, twos, threes := 0, 0, 0

    for _, num := range nums {
        twos = twos | (ones & num)
        ones = ones ^ num
        threes = ones & twos
        ones =  ones & (^threes)
        twos = twos & (^threes)
    }

    return ones
}

Count Complete Tree Nodes

Given a complete binary tree, count the number of nodes.

Note:

Definition of a complete binary tree from Wikipedia:

In a complete binary tree every level, except possibly the last, is completely filled, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Example:

1
2
3
4
5
6
7
8
Input:
    1
   / \
  2   3
 / \  /
4  5 6

Output: 6

Explanation

  1. Get the left most’s height and right most’s height. If they are equal, then the tree is a full binary tree, which means all nodes have two children except the leaves nodes. So a full binary tree has total $2^h-1$ nodes.

  2. If the left most height and right most height are not equal, we can recursivly call this method for the left child and also call this method for the right child, also plus one which is for the root node.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func countNodes(root *TreeNode) int {
    if root == nil { return 0 }

    leftPtr, rightPtr := root, root
    leftHeight, rightHeight := 0, 0

    for leftPtr != nil {
        leftHeight += 1
        leftPtr = leftPtr.Left
    }
    for rightPtr != nil {
        rightHeight += 1
        rightPtr = rightPtr.Right
    }

    if leftHeight == rightHeight {
        return 1 << leftHeight - 1
    }

    return 1 + countNodes(root.Left) + countNodes(root.Right)
}

Unique Binary Search Trees

Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?

Example:

1
2
3
4
5
6
7
8
9
10
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

Explanation

  1. We can use dynamic programming to solve this problem.

  2. Dynamic state is a one dimensional array, dp[n] means when input is n, the total number of unique BST.

  3. Dynamic init is dp[0] = 1, dp[1] = 1. For example, when n is 1, we only have one way to struct the unique BST.

  4. Dynamic function. When n = 2, the total number of unqiue BST is 2, in other word, the root node can be 1, right node can be 2; or root node is 2, left node is 1. When n = 3, we have three cases: when root node is element 1, there is 0 node on the left and there are 2 nodes on the right; when root node element is 2, there is 1 node on the left and 1 node on the right; when root node is element 3, there are 2 nodes on the left and 0 node on the right. We can illustrate it below:

    1
    2
    3
            1        2        3
       / \      / \      /  \
      0   2    1   1    2    0

  5. From the above illustration, input n=3, when root node is element 1, it can only have 0 node on the left and 2 nodes on the right, and there are 2 unique ways because dp[0] = 1, dp[2] = 2, and 1 * 2 = 2. When root node is element 2, there is one node on the left and one on the right, and there is 1 unique way because dp[1] = 1, 1 * 1 = 1. When root node is element 3, there are two node on the left and zero node on the right, and there are 2 unique ways because dp[2] = 2, dp[0] = 1, 2 * 1 = 2. Therefore, when input is 3, we have dp[0]*dp[2] + dp[1]*dp[1] + dp[2]*dp[0] = 5 unique ways. So, when input is n, if there is 0 node on the left, then there are n-1 node on the right because we need to subtract there is 1 root node.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
func numTrees(n int) int {
    dp := make([]int, n + 1)
    dp[0] = 1
    dp[1] = 1

    for i := 2; i <= n; i++ {
        for j := 0; j < i; j++ {
            dp[i] += dp[j] * dp[i-1-j]
        }
    }

    return dp[n]
}

Find the Duplicate Number

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Example 1:

1
2
Input: [1,3,4,2,2]
Output: 2

Example 2:

1
2
Input: [3,1,3,4,2]
Output: 3

Note:

  1. You must not modify the array (assume the array is read only).

  2. You must use only constant, O(1) extra space.

  3. Your runtime complexity should be less than O(n2).

  4. There is only one duplicate number in the array, but it could be repeated more than once.

Explanation 1

  1. If we can modify the array, then we loop through the array, and each iteration we add m = len(nums) to nums[nums[i]]. For example, if the input array is [1, 3, 4, 2, 2]. After this loop, we have [1, 8, 14, 7, 7]. The unique number will be less than 2 * len(nums). If the number is more than 2 * len(nums) and it’s the maximum number, then this maximum number’s index is the duplicated number, whiich is 2 in this example. We can reverse this array to the original array by module each number by len(nums).

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func findDuplicate(nums []int) int {
    m := len(nums)
    for i := range nums {
        idx := nums[i] % m
        nums[idx] += m
    }

    curMax, curMaxIdx := 0, 0
    for i := range nums {
        if nums[i] > curMax {
            curMax = nums[i]
            curMaxIdx = i
        }
        nums[i] = nums[i] % m
    }

    return curMaxIdx
}

Explanation 2

  1. This problem can use the same technique as 142. Linked List Cycle II since there are duplicated number in the array and each integer is between 1 and n (inclusive), it must have a cycle. For example, if the input is [1, 2, 3, 4, 2], we have (both the duplicated number 2 are pointing to 3):

    1
    2
    3
     1->2->3->4->2
       |     |
       <------

  2. Initialize slow and fast be 0, then slow moves one step, slow = nums[slow];fast moves two steps, fast = nums[fast]; fast = nums[fast], in other words, fast = nums[nums[fast]]. Repeat this step, until slow = fast, which is their meeting point.

  3. Then, slow set to 0 instead of nums[0] because in 142. Linked List Cycle II this method, we find the cycle starting point which is 3 in the above example, but now we want to find the point that is one step before the the cycle starting point, so we set slow to 0. Now slow and fast move at the same speed, this time their meeting point is the point before the meeting point, which is the duplicated number.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func findDuplicate(nums []int) int {
    slow, fast := 0, 0
    for true {
        slow = nums[slow]
        fast = nums[nums[fast]]
        if slow == fast { break }
    }
    slow = 0
    for slow != fast {
        slow = nums[slow]
        fast = nums[fast]
    }
    return slow
}

Sum Root to Leaf Numbers

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:

1
2
3
4
5
6
7
8
9
Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Explanation

  1. We can use recursion method to solve. Whenever we encounted a root value, we will multiple the previous sum by 10 then add the current root value to become a new sum.

  2. We can think of the left node as a root, the right node as a root, then solve them recursivly and pass the new sum as left child and right child’s previous sum to the helper method to get their sums and add them both to become the root’s sum.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumNumbers(root *TreeNode) int {
    return helper(root, 0)
}

func helper(root *TreeNode, pre int) int {
    if root == nil { return 0 }
    pre = pre * 10 + root.Val
    if root.Left == nil && root.Right == nil { return pre }
    return helper(root.Left, pre) + helper(root.Right, pre)
}

Perfect Squares

Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, ...) which sum to n.

Example 1:

1
2
3
Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.

Example 2:

1
2
3
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

Explanation

  1. We can solve this problem using dynamic programming. Dynamic state is creating an one dimensional array dp has length n+1 since if n=5, array will start have index 0, 1, 2, 3, 4, 5. dp[i] means the numOfPerfectSquares for i, so the result we will return is dp[5].

  2. Dynamic init is dp[i] = i since every positive number n can be formed by n number of perfect square 1.

  3. Dynamic function will be dp[i] = min(dp[i], dp[i - j*j] + 1, the j means loop from 1 until j*j <= i. We plus one because dp[j*j] = 1. For example, dp[5] = dp[5-1*1]+1 = dp[4]+1 = 2, dp[5] can also be dp[5-2*2]+1 = dp[1]+1 = 2. The base case is dp[0]=0 if i == j*j, then dp[i] = dp[0]+1=1.

  4. Dynamic result is dp[n].

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func numSquares(n int) int {
    dp := make([]int, n + 1)

    for i := 1; i <= n; i++ {
        dp[i] = i
        j := 1
        for j * j <= i {
            dp[i] = min(dp[i], dp[i - j*j] + 1)
            j += 1
        }
    }

    return dp[n]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Reconstruct Itinerary

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

  1. If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].

  2. All airports are represented by three capital letters (IATA code).

  3. You may assume all tickets form at least one valid itinerary.

  4. One must use all the tickets once and only once.

Example 1:

1
2
Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]

Example 2:

1
2
3
4
Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"].
             But it is larger in lexical order.

Explanation

  1. First, we should construct a graph adjacency list using a HashMap hm<String, PriorityQueue<String>>.

  2. Then we use DFS passing the starting point JFK as parameter. Inside this DFS, we iterate this priority queue hm.get(startingPoint), poll out the first String in the priority queue (remove the edge so don’t repeat) and pass it to the recursive DFS method. The base case is If hm.get(startingPoint) is NULL, which means it’s the end point, then we add it in front of the result list.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func findItinerary(tickets [][]string) []string {
    sort.Slice(tickets, func (i, j int) bool {
        return tickets[i][1] < tickets[j][1]
    })
    adjLst := make(map[string][]string)

    for _, ticket := range tickets {
        from := ticket[0]
        to := ticket[1]
        adjLst[from] = append(adjLst[from], to)
    }

    res := make([]string, 0)
    dfs("JFK", adjLst, &res)
    return res
}

func dfs(from string, adjLst map[string][]string, res *[]string) {
    for len(adjLst[from]) > 0 {
        to := adjLst[from][0]
        adjLst[from] = adjLst[from][1:]
        dfs(to, adjLst, res)
    }
    *res = prepend(*res, from)
}

func prepend(slice []string, ele string) []string {
    slice = append(slice, "")
    copy(slice[1:], slice)
    slice[0] = ele
    return slice
}

Week 5: June 29th–June 30th

Unique Paths

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

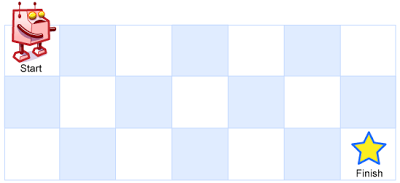
Unique Paths

Above is a 7 x 3 grid. How many possible unique paths are there?

Example 1:

1
2
3
4
5
6
7
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

1
2
Input: m = 7, n = 3
Output: 28

Constraints:

  1. 1 <= m, n <= 100

  2. It’s guaranteed that the answer will be less than or equal to 2 * 10 ^ 9.

Explanation

  1. We can solve this whole problem by solving the subproblem, so we can use dynamic programming.

  2. We can make a tow dimensional array dp[row][col] representing that the total steps reach the coordinate of row and col. And dp[row][col] = dp[row-1][col] + dp[row][col-1] which means the total steps of reaching the current coordinate is equal to the steps reaching the top row plus the steps reaching the left column.

  3. The base case is reaching any coordinate of the first row is always 1, and reaching the first column is also always 1.

  4. Now we can just find out the value of dp[row-1][col-1].

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func uniquePaths(m int, n int) int {
    dp := make([][]int, n)
    for i := range dp {
        dp[i] = make([]int, m)
    }

    for r := 0; r < len(dp); r++ {
        dp[r][0] = 1
    }
    for c := 0; c < len(dp[0]); c++ {
        dp[0][c] = 1
    }

    for r := 1; r < len(dp); r++ {
        for c := 1; c < len(dp[0]); c++ {
            dp[r][c] = dp[r-1][c] + dp[r][c-1]
        }
    }

    return dp[len(dp)-1][len(dp[0])-1]
}

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func uniquePaths(m int, n int) int {
    dp := make([]int, m)
    for i := range dp {
        dp[i] = 1
    }

    for r := 1; r < n; r++ {
        for c := 1; c < m; c++ {
            dp[c] = dp[c] + dp[c-1]
        }
    }

    return dp[m-1]
}

Word Search II

Given a 2D board and a list of words from the dictionary, find all words in the board.

Each word must be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example:

1
2
3
4
5
6
7
8
9
10
Input:
board = [
  ['o','a','a','n'],
  ['e','t','a','e'],
  ['i','h','k','r'],
  ['i','f','l','v']
]
words = ["oath","pea","eat","rain"]

Output: ["eat","oath"]

Note:

  1. All inputs are consist of lowercase letters a-z.

  2. The values of words are distinct.

Hint 1:

You would need to optimize your backtracking to pass the larger test. Could you stop backtracking earlier?

Hint 2:

If the current candidate does not exist in all words’ prefix, you could stop backtracking immediately. What kind of data structure could answer such query efficiently? Does a hash table work? Why or why not? How about a Trie? If you would like to learn how to implement a basic trie, please work on this problem: Implement Trie (Prefix Tree) first.

Explanation

  1. We can also use Trie to solve this problem. First, insert all words into the trie. Then loop through the board’s every character. For each character, we use DFS to check if the Trie has this character as a children. If not, then return. Else, we mark the character as visited; append this character into the current string; if this character in the trie is the end of word, then we add the updated current string into the result set. Next, we keep DFS with the updated string, updated Trie pointer and updated position. After DFS of the 4 directions, we restore the visited character as unvisited.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
func findWords(board [][]byte, words []string) []string {
    trie := Constructor()

    for _, word := range words {
        trie.Insert(word)
    }

    resSet := make(map[string]bool)

    for r := 0; r < len(board); r++ {
        for c := 0; c < len(board[0]); c++ {
            dfs(board, r, c, &trie, "", resSet)
        }
    }

    res := make([]string, 0)
    for word := range resSet {
        res = append(res, word)
    }

    return res
}


func dfs(board [][]byte, r int, c int, trie *Trie, cur string, resSet map[string]bool) {
    if r < 0 || r >= len(board) || c < 0 || c >= len(board[0]) { return }
    if board[r][c] == '#' { return }
    if trie.children[board[r][c] - 'a'] == nil { return }

    ch := board[r][c]
    board[r][c] = '#'
    updatedCur := cur + string([]byte{ch})

    if trie.children[ch - 'a'].isEnd { resSet[updatedCur] = true }

    dfs(board, r + 1, c, trie.children[ch - 'a'], updatedCur, resSet)
    dfs(board, r - 1, c, trie.children[ch - 'a'], updatedCur, resSet)
    dfs(board, r, c + 1, trie.children[ch - 'a'], updatedCur, resSet)
    dfs(board, r, c - 1, trie.children[ch - 'a'], updatedCur, resSet)

    board[r][c] = ch
}


type Trie struct {
    children []*Trie
    isEnd bool
}


/** Initialize your data structure here. */
func Constructor() Trie {
    return Trie{make([]*Trie, 26), false}
}


/** Inserts a word into the trie. */
func (this *Trie) Insert(word string)  {
    cur := this
    for _, ch := range word {
        if cur.children[ch - 'a'] == nil {
            cur.children[ch - 'a'] = &Trie{make([]*Trie, 26), false}
        }
        cur = cur.children[ch - 'a']
    }
    cur.isEnd = true
}