[LeetCode] 84. Largest Rectangle in Histogram

Posted on | In

Problem

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

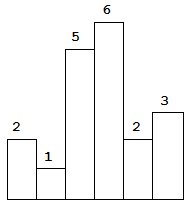
84. Largest Rectangle in Histogram

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

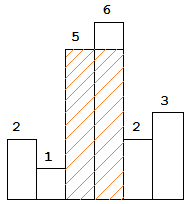
84. Largest Rectangle in Histogram

The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

1
2
Input: [2,1,5,6,2,3]
Output: 10

Explanation 1

  1. Iterate each element, if the next element is less than the current element or we hit the end of the array, then we start to find the rectangle’s area and that rectangle’s right side is fixed on current index.

  2. We can find the min height by loop backward from the current index to zero, and we multiple the width with the minHeight.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) return 0;
        int max = 0;
        for (int cur = 0; cur < heights.length; cur++) {
            if (cur == heights.length-1 || heights[cur+1] < heights[cur]) {
                int minHeight = heights[cur];
                for (int i = cur; i >= 0; i--) {
                    int width = cur - i + 1;
                    minHeight = Math.min(minHeight, heights[i]);
                    max = Math.max(max, width * minHeight);
                }
            }
        }
        
        return max;
    }
}

Explanation 2

  1. We can find the area by finding the current element’s leftMost and rightMost index and area = heights[cur] * (rightMost-leftMost-1). From the above example, if the current element is at index 2, its height is 5. Then the leftMost is at index 1, and rightMost is at index 4 (leftMost is the previous first index element height that is less than the current element height, rightMost is the next first index element height that is less than the current element height). So, when current index is 2, its maximum area is 5 * (4-1-1) = 10 which shows the red area. Another example is when current index is 3 which is at height 6, its maximum area is 6 * (4-2-1) = 6.

  2. We can create a ascending stack to hold the ascending height’s element index. Iterating each element, when the curent element height is greater than the stack’s top height, then we push it to the stack. Else, we set the current element’s index to be the rightMost, we pop the top index of the stack and let it be ind, leftMost will now be the peek of the stack, then we use the above method to calculate the max area. The current index needs to stay the same and we need to compare it with the top of the stack to determine if we need to push it to the stack or not. If not, then we pop find out the rightMost and leftMost and calcualte the area again.

  3. After we finish iterating, if the stack is not empty, then we set the rightMost to the stack’s top index plus one. ind is the pop element of the stack, leftMost is the peek element of the stack or -1 if stack is empty. We calcualte the max area again until the stack is empty.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) return 0;
        Stack<Integer> st = new Stack<>();
        int max = 0;
        for (int i = 0; i < heights.length; i++) {
            if (st.isEmpty() || heights[i] >= heights[st.peek()]) {
                st.push(i);
            } else {
                int rightMost = i;
                int ind = st.pop();
                while (!st.isEmpty() && heights[st.peek()] == heights[ind]) {
                    ind = st.pop();
                }
                int leftMost = st.isEmpty() ? -1 : st.peek();
                max = Math.max(max, heights[ind] * (rightMost-leftMost-1));
                i--;
            }
        }
        
        int rightMost = st.peek()+1;
        while (!st.isEmpty()) {
            int ind = st.pop();
            while (!st.isEmpty() && heights[st.peek()] == heights[ind]) {
                ind = st.pop();
            }
            int leftMost = st.isEmpty() ? -1 : st.peek();
            max = Math.max(max, heights[ind] * (rightMost-leftMost-1));
        }
        
        return max;
    }
}