[LeetCode] 62. Unique Paths

Posted on | In

Problem

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

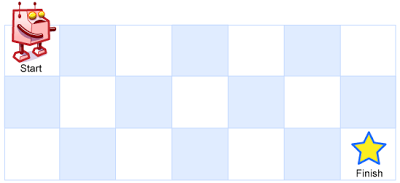
62. Unique Paths

Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

1
2
3
4
5
6
7
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

1
2
Input: m = 7, n = 3
Output: 28

Explanation

  1. We can solve this whole problem by solving the subproblem, so we can use dynamic programming.

  2. We can make a tow dimensional array dp[row][col] representing that the total steps reach the coordinate of row and col. And dp[row][col] = dp[row-1][col] + dp[row][col-1] which means the total steps of reaching the current coordinate is equal to the steps reaching the top row plus the steps reaching the left column.

  3. The base case is reaching any coordinate of the first row is always 1, and reaching the first column is also always 1.

  4. Now we can just find out the value of dp[row-1][col-1].

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    void helper(int[][] memo) {
        for (int c = 0; c < memo[0].length; c++) {
            memo[0][c] = 1;
        }
        for (int r = 0; r < memo.length; r++) {
            memo[r][0] = 1;
        }

        for (int r = 1; r < memo.length; r++) {
            for (int c = 1; c < memo[0].length; c++) {
                memo[r][c] = memo[r-1][c] + memo[r][c-1];
            }
        }
    }

    public int uniquePaths(int m, int n) {
        int[][] memo = new int[n][m];
        helper(memo);
        return memo[n-1][m-1];
    }
}

// class Solution {
//     public int uniquePaths(int m, int n) {
//         int[] memo = new int[m];
//         Arrays.fill(memo, 1);

//         for (int r = 1; r < n; r++) {
//             for (int c = 1; c < m; c++) {
//                 memo[c] += memo[c-1];
//             }
//         }

//         return memo[memo.length-1];
//     }
// }