May LeetCoding Challenge

Posted on | In

The shelter-in-place order was extended to the end of May. LeetCode also published this May LeetCoding Challenge. Let’s continue this one day one go problem.

Week 1: May 1st–May 7th

First Bad Version

You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.

Suppose you have n versions [1, 2, ..., n] and you want to find out the first bad one, which causes all the following ones to be bad.

You are given an API bool isBadVersion(version) which will return whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.

Example:

1
2
3
4
5
6
7
Given n = 5, and version = 4 is the first bad version.

call isBadVersion(3) -> false
call isBadVersion(5) -> true
call isBadVersion(4) -> true

Then 4 is the first bad version.

Explanation

  1. We can use binary search to find the first bad version.

  2. The range is 1 to n inclusive. While left < right, we find the mid number. If the mid number is not a bad version, then update left = mid + 1. Else, we update right = mid. Outside the while loop, we check if left is a bad version. If it’s a bad version, we return left, else return -1.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Forward declaration of isBadVersion API.
 * @param   version   your guess about first bad version
 * @return 	 	      true if current version is bad
 *			          false if current version is good
 * func isBadVersion(version int) bool;
 */

func firstBadVersion(n int) int {
    left, right := 1, n
    for left < right {
        mid := left + (right - left) / 2
        if !isBadVersion(mid) {
            left = mid + 1
        } else {
            right = mid
        }
    }
    if isBadVersion(left) {
        return left
    } else {
        return -1
    }
}

Jewels and Stones

You’re given strings J representing the types of stones that are jewels, and S representing the stones you have. Each character in S is a type of stone you have. You want to know how many of the stones you have are also jewels.

The letters in J are guaranteed distinct, and all characters in J and S are letters. Letters are case sensitive, so "a" is considered a different type of stone from "A".

Example 1:

1
2
Input: J = "aA", S = "aAAbbbb"
Output: 3

Example 2:

1
2
Input: J = "z", S = "ZZ"
Output: 0

Note:

  • S and J will consist of letters and have length at most 50.

  • The characters in J are distinct.

Hint 1:

For each stone, check if it is a jewel.

Explanation

  1. First put all the characters in J to a set. Then loop through all characters in S, if the current character is inside the set, we inrease the result. After finishing looping all characters in S, return the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
func numJewelsInStones(J string, S string) int {
    res := 0
    set := make(map[byte]bool)
    for i := 0; i < len(J); i++ {
        set[J[i]] = true
    }
    for i := 0; i < len(S); i++ {
        if _, ok := set[S[i]]; ok {
            res += 1
        }
    }
    return res
}

Ransom Note

Given an arbitrary ransom note string and another string containing letters from all the magazines, write a function that will return true if the ransom note can be constructed from the magazines ; otherwise, it will return false.

Each letter in the magazine string can only be used once in your ransom note.

Note:

You may assume that both strings contain only lowercase letters.

1
2
3
canConstruct("a", "b") -> false
canConstruct("aa", "ab") -> false
canConstruct("aa", "aab") -> true

Explanation 1

  1. We can solve it by putting all magazine’s characters into a HashMap. Then loop through the ransomNote characters, every iteration, we subtract the corresponding character’s frequency in the map. If the current character is not in the map, we return false; or if map’s frequency becomes negative we return false. At the end, outside of the loop, we return true.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func canConstruct(ransomNote string, magazine string) bool {
    hm := make(map[rune]int)
    for _, ch := range magazine {
        hm[ch]++
    }
    for _, ch := range ransomNote {
        if hm[ch] == 0 {
            return false
        } else {
            hm[ch]--
        }
    }
    return true
}

Explanation 2

  1. Another way is count the ransomNote character frequency first, cnt is equal to the total characters in the ransomNote, and we store the frequency in an int array that has size 26.

  2. Then loop through the characters in magazine, if the current character in the integer array has frequency more than 1, then we decrease its frequency and decrease cnt. If cnt is equal to 0, that means we have all the characters we need to generate the ransomNote, so we return true. At the end, we return cnt == 0.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func canConstruct(ransomNote string, magazine string) bool {
    if len(ransomNote) > len(magazine) {
        return false
    }
    hm := make([]int32, 26)
    cnt := 0
    for _, ch := range ransomNote {
        hm[ch - int32('a')]++
        cnt++
    }
    for _, ch := range magazine {
        if hm[ch - int32('a')] > 0 {
            hm[ch - int32('a')]--
            cnt--
        }
        if cnt == 0 {
            return true
        }
    }
    return cnt == 0
}

Number Complement

Given a positive integer, output its complement number. The complement strategy is to flip the bits of its binary representation.

Example 1:

1
2
3
Input: 5
Output: 2
Explanation: The binary representation of 5 is 101 (no leading zero bits), and its complement is 010. So you need to output 2.

Example 2:

1
2
3
Input: 1
Output: 0
Explanation: The binary representation of 1 is 1 (no leading zero bits), and its complement is 0. So you need to output 0.

Note:

  1. The given integer is guaranteed to fit within the range of a 32-bit signed integer.

  2. You could assume no leading zero bit in the integer’s binary representation.

  3. This question is the same as 1009: https://leetcode.com/problems/complement-of-base-10-integer/

Explanation 1

  1. First, we need to find the left most bit that is equals to 1, then start from that bit to the lowest bit, for each bit, we can XOR the current bit with 1 to revert from 0 to 1, 1 to 0.

  2. We can find the left most bit that is equals to 1 by starting from the highest bit, use AND operation to AND the input num with 1 << 31, 1 << 30, 1 << 29 … until the AND result is 1.

Solution 1

1
2
3
4
5
6
7
8
9
10
func findComplement(num int) int {
    foundOne := false
    for i := 31; i >= 0; i-- {
        if num & (1 << i) != 0 { foundOne = true }
        if foundOne {
            num = num ^ (1 << i)
        }
    }
    return num
}

Explanation 2

  1. We can use the NOT operator to NOT the input number, but for the leading zero, we dont’ want to revert. We can use a mask represented by all bits equals to 1 to mask all the leading zero. For example, if the input number is 000101, then the mask will be 111000. After we get the mask, we can NOT the mask, NOT the input number, then AND these two results.

  2. We can find the mask by first initialize the mask be the maximum integer, which means all 32 bits are 1. Then while the mask AND the input number is 1, we left shift the mask until the AND result is 0.

Solution 2

1
2
3
4
5
6
7
func findComplement(num int) int {
    mask := ^0
    for mask & num != 0 {
        mask = mask << 1
    }
    return ^mask & ^num
}

First Unique Character in a String

Given a string, find the first non-repeating character in it and return it’s index. If it doesn’t exist, return -1.

Examples:

1
2
3
4
5
s = "leetcode"
return 0.

s = "loveleetcode",
return 2.

Note: You may assume the string contain only lowercase letters.

Explanation

  1. Create a map with character and its frequency.

  2. Loop through the characters in the string, if the iterated character’s frequency is 1, return its index.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
func firstUniqChar(s string) int {
    letters := make([]int, 26)
    for _, ch := range s {
        letters[ch - 'a']++
    }
    for i, ch := range s {
        if letters[ch - 'a'] == 1 {
            return i
        }
    }
    return -1
}

Majority Element

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

1
2
Input: [3,2,3]
Output: 3

Example 2:

1
2
Input: [2,2,1,1,1,2,2]
Output: 2

Explanation

  1. Using Moore Voting algorithm, initialize the first number be the result, count is 1. When we hit the second number, if the second number is equal to the first number, then we just increase count by 1. Else if the second number is not the same, then we decreae the count by 1. When we hit the next number, if the count is 0, then we update result to be that number and increase count by 1.

  2. This method only works when the majority element has more than half number of the elements.

From: [LeetCode] 169. Majority Element

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func majorityElement(nums []int) int {
    res := nums[0]
    cnt := 0
    for _, num := range nums {
        if cnt == 0 {
            res = num
            cnt += 1
        } else if num == res {
            cnt += 1
        } else {
            cnt -= 1
        }
    }
    return res
}

Cousins in Binary Tree

In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1.

Two nodes of a binary tree are cousins if they have the same depth, but have different parents.

We are given the root of a binary tree with unique values, and the values x and y of two different nodes in the tree.

Return true if and only if the nodes corresponding to the values x and y are cousins.

Example 1:

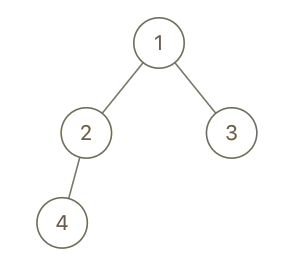
Cousins in Binary Tree 1

1
2
Input: root = [1,2,3,4], x = 4, y = 3
Output: false

Example 2:

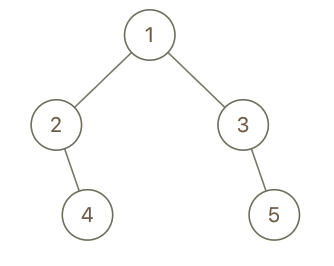
Cousins in Binary Tree 2

1
2
Input: root = [1,2,3,null,4,null,5], x = 5, y = 4
Output: true

Example 3:

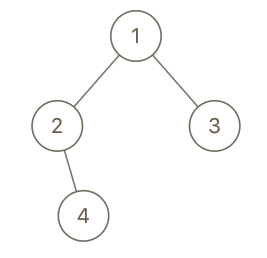
Cousins in Binary Tree 3

1
2
Input: root = [1,2,3,null,4], x = 2, y = 3
Output: false

Note:

  1. The number of nodes in the tree will be between 2 and 100.

  2. Each node has a unique integer value from 1 to 100.

Explanation 1

  1. We can use DFS to solve this problem by getting the depth of x and y and compare their depths. Inside the same DFS function, we can also get their parents. At the end, we compare x and y’s depths if they are equal, and parents if they are not equal.

  2. In the main function, we create two arrays depths[] and parents[] both have size two to record x and y’s depths and parents. We pass these two arrays into the dfs function, as well as the current depth 0 and current parent null, and root, x and y.

  3. In the DFS function, the base case is if the root == NULL, then we return immediately. If root.val == x, then we update x's depth depths[0] = curDepth and x’s parent parents[0] = curParent. Similarly for if root.val == y. Else, we recursively check the root’s left child and right child, and we update the curDepth += 1 and curParent = root.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isCousins(root *TreeNode, x int, y int) bool {
    tempX, tempY := -1, -1
    xDepth, yDepth := &tempX, &tempY
    xParent := &TreeNode{}
    yParent := &TreeNode{}
    dfs(root, x, y, 0, nil, xDepth, yDepth, xParent, yParent)
    return *xDepth == *yDepth && *xParent != *yParent
}

func dfs(root *TreeNode, x, y, curDepth int, curParent *TreeNode, xDepth, yDepth *int, xParent, yParent *TreeNode) {
    if root == nil { return }
    if *xDepth != -1 && curDepth > *xDepth || *yDepth != -1 && curDepth > *yDepth { return }
    if root.Val == x {
        *xDepth = curDepth
        if curParent != nil {
            *xParent = *curParent
        }
    } else if root.Val == y {
        *yDepth = curDepth
        if curParent != nil {
            *yParent = *curParent
        }
    } else {
        dfs(root.Left, x, y, curDepth + 1, root, xDepth, yDepth, xParent, yParent)
        dfs(root.Right, x, y, curDepth + 1, root, xDepth, yDepth, xParent, yParent)
    }
}

Explanation 2

  1. We can also solve this problem by using BFS. First, we create a queue to store the current level’s TreeNodes and push the root node to the queue. Also, we create two variables hasX and hasY to represent if we found the TreeNode that has value x and y.

  2. While the queue is not empty, we loop through the size of the current level and each time we poll out a node pollNode. First we check if x and y both have the same parent, so we check if pollNode’s left child and right child, if their node’s value is equal to x and y, then we return false because x and y have the same parent pollNode. Next, we check if the pollNode’s value is equal to x or y, then we mark hasX or hasY be true. After finish looping the current level, we check if both hasX and hasY are true, if they both are true, then we return true immdediately. If only one of them is true we return false because x and y are not in the same depth. After we checking all the nodes, or the queue is empty, we return false.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isCousins(root *TreeNode, x int, y int) bool {
    hasX, hasY := false, false
    queue := make([]*TreeNode, 0)
    queue = append(queue, root)
    for len(queue) != 0 {
        for i := len(queue); i > 0; i-- {
            pollNode := queue[0]
            queue = queue[1:len(queue)]
            if pollNode.Left != nil && pollNode.Right != nil {
                if pollNode.Left.Val == x && pollNode.Right.Val == y { return false }
                if pollNode.Left.Val == y && pollNode.Right.Val == x { return false }
            }
            if pollNode.Val == x { hasX = true }
            if pollNode.Val == y { hasY = true }
            if pollNode.Left != nil {
                queue = append(queue, pollNode.Left)
            }
            if pollNode.Right != nil {
                queue = append(queue, pollNode.Right)
            }
        }
        if hasX != hasY { return false }
        if hasX && hasY { return true }
    }
    return false
}

Explanation 3

  1. Another DFS solution using Go.

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isCousins(root *TreeNode, x int, y int) bool {
    depthX, parentX, _ := dfs(root, x, 0, root)
    depthY, parentY, _ := dfs(root, y, 0, root)
    return depthX == depthY && parentX != parentY
}

func dfs(root *TreeNode, x, curDepth int, curParent *TreeNode) (int, *TreeNode, *TreeNode) {
    if root == nil || root.Val == x {
        return curDepth, curParent, root
    }
    if depth, parent, foundNode := dfs(root.Left, x, curDepth + 1, root); foundNode != nil {
        return depth, parent, foundNode
    }
    return dfs(root.Right, x, curDepth + 1, root)
}

Week 2: May 8th–May 14th

Check If It Is a Straight Line

You are given an array coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.

Example 1:

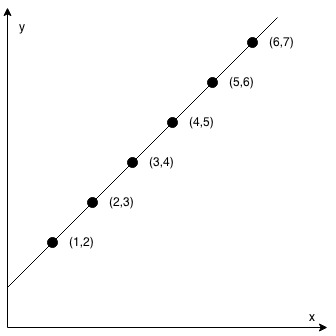
Check If It Is a Straight Line 1

1
2
Input: coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
Output: true

Example 2:

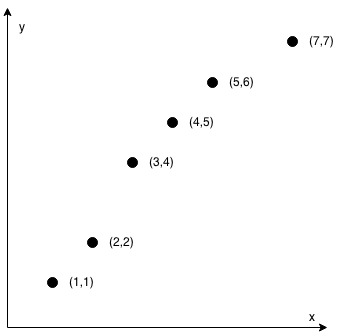
Check If It Is a Straight Line 2

1
2
Input: coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
Output: false

Constraints:

  • 2 <= coordinates.length <= 1000

  • coordinates[i].length == 2

  • -10^4 <= coordinates[i][0], coordinates[i][1] <= 10^4

  • coordinates contains no duplicate point.

Hint 1:

If there’re only 2 points, return true.

Hint 2:

Check if all other points lie on the line defined by the first 2 points.

Hint 3:

Use cross product to check collinearity.

Explanation 1

  1. If there are only two points, we can return true.

  2. We can calculate the slope for the first two points, then loop through the input coordinates, calculate every current point with the first point’s slope and compare this slope with the first two points’ slope. If they are not match, we can return false immediately. Outside the loop, we return true.

  3. Since the denominator cannot be 0, in the calculate slope function, we can return -1 if two points have the same x-value.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func checkStraightLine(coordinates [][]int) bool {
    if len(coordinates) == 2 { return true }
    slope := getSlope(coordinates[0], coordinates[1])
    for i := 2; i < len(coordinates); i++ {
        if slope != getSlope(coordinates[0], coordinates[i]) {
            return false
        }
    }
    return true
}

func getSlope(c1, c2 []int) float32 {
    if c2[0] - c1[0] == 0 { return -1 }
    return float32(c2[1] - c1[1]) / float32(c2[0] - c1[0])
}

Explanation 2

  1. To avoid dividing by 0, we can also use cross product. For example:

    1
    2
    3
     y2 - y1   y3 - y1
 ------- = ------- =====> (y2 - y1) * (x3 - x1) = (x2 - x1) * (y3 - y1)
 x2 - x1   x3 - x1

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
func checkStraightLine(coordinates [][]int) bool {
    if len(coordinates) == 2 { return true }
    for i := 0; i < len(coordinates) - 2; i += 2 {
        if !crossProduct(coordinates[i], coordinates[i + 1], coordinates[i + 2]) {
            return false
        }
    }
    return true
}

func crossProduct(c1, c2, c3 []int) bool {
    return (c2[1] - c1[1]) * (c3[0] - c1[0]) == (c2[0] - c1[0]) * (c3[1] - c1[1])
}

Valid Perfect Square

Given a positive integer num, write a function which returns True if num is a perfect square else False.

Note: Do not use any built-in library function such as sqrt.

Example 1:

1
2
Input: 16
Output: true

Example 2:

1
2
Input: 14
Output: false

Explanation 1

  1. We can use binary search to solve this problem. First we get the middle number, compare $mid*mid == num$, if they are equal, we return true; else if mid*mid < num, we increase left = mid + 1; else if mid * mid > num, we decrease right = mid - 1. At the end, when left == right, we compare the last time left * left == num.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func isPerfectSquare(num int) bool {
    left, right := 1, num
    for left <= right {
        mid := left + (right - left) / 2
        if mid * mid == num {
            return true
        } else if mid * mid < num {
            left = mid + 1
        } else {
            right = mid - 1
        }
    }
    return false
}

Explanation 2

  1. For every perfect square number, we have:

    1
    2
    3
    4
    5
    6
     1 = 1
 4 = 1 + 3
 9 = 1 + 3 + 5
 16 = 1 + 3 + 5 + 7
 25 = 1 + 3 + 5 + 7 + 9
 36 = 1 + 3 + 5 + 7 + 9 + 11

  2. From the above pattern, we can have num -= 1, num -= 3, num -= 5, etc. If num == 0 Then num is a perfect square, else we return false.

Solution 2

1
2
3
4
5
6
7
8
func isPerfectSquare(num int) bool {
    i := 1
    for num > 0 {
        num -= i
        i += 2
    }
    return num == 0
}

Find the Town Judge

In a town, there are N people labelled from 1 to N. There is a rumor that one of these people is secretly the town judge.

If the town judge exists, then:

  1. The town judge trusts nobody.

  2. Everybody (except for the town judge) trusts the town judge.

  3. There is exactly one person that satisfies properties 1 and 2. You are given trust, an array of pairs trust[i] = [a, b] representing that the person labelled a trusts the person labelled b.

If the town judge exists and can be identified, return the label of the town judge. Otherwise, return -1.

Example 1:

1
2
Input: N = 2, trust = [[1,2]]
Output: 2

Example 2:

1
2
Input: N = 3, trust = [[1,3],[2,3]]
Output: 3

Example 3:

1
2
Input: N = 3, trust = [[1,3],[2,3],[3,1]]
Output: -1

Example 4:

1
2
Input: N = 3, trust = [[1,2],[2,3]]
Output: -1

Example 5:

1
2
Input: N = 4, trust = [[1,3],[1,4],[2,3],[2,4],[4,3]]
Output: 3

Note:

  1. 1 <= N <= 1000

  2. trust.length <= 10000

  3. trust[i] are all different

  4. trust[i][0] != trust[i][1]

  5. 1 <= trust[i][0], trust[i][1] <= N

Explanation 1

  1. The town judge trust 0 people, and N - 1 people trust the town judge. This is like a graph problem, we need to find a vertex that its out-degree is 0, its in-degree is N - 1.

  2. We can create two array outDegree and inDegree both have size N + 1, and outDegree[i] represent the number of people the ith person trust, and inDegree[i] represent the number of people trust the ith person. Loop through the input array and look for outDegree[i] == 0 && inDegree[i] == N-1, then i is the town judge.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
func findJudge(N int, trust [][]int) int {
    inDegree, outDegree := make([]int, N+1), make([]int, N+1)
    for _, arr := range trust {
        outDegree[arr[0]] += 1
        inDegree[arr[1]] += 1
    }
    for i := 1; i <= N; i++ {
        if outDegree[i] == 0 && inDegree[i] == N - 1 {
            return i
        }
    }
    return -1
}

Explanation 2

  1. We can solve this problem by using only one array cnt, and cnt[i] represents number of people trust i. Loop through the input array, we update cnt[arr[0]] -= 1 and cnt[arr[1]] += 1. Since there are no duplicate entries in the input array, a person can only be trusted by a maximum of N-1 people. If this person trusts anyone, then it would not be able to have value of N-1 and this is why we reduct 1 for index arr[0]. At the end, if cnt[i] == N - 1, then i is the town judge.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
func findJudge(N int, trust [][]int) int {
    cnt := make([]int, N+1)
    for _, arr := range trust {
        cnt[arr[0]] -= 1
        cnt[arr[1]] += 1
    }
    for i := 1; i <= N; i++ {
        if cnt[i] == N - 1 {
            return i
        }
    }
    return -1
}

Flood Fill

An image is represented by a 2-D array of integers, each integer representing the pixel value of the image (from 0 to 65535).

Given a coordinate (sr, sc) representing the starting pixel (row and column) of the flood fill, and a pixel value newColor, “flood fill” the image.

To perform a “flood fill”, consider the starting pixel, plus any pixels connected 4-directionally to the starting pixel of the same color as the starting pixel, plus any pixels connected 4-directionally to those pixels (also with the same color as the starting pixel), and so on. Replace the color of all of the aforementioned pixels with the newColor.

At the end, return the modified image.

Example 1:

1
2
3
4
5
6
7
8
9
Input:
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
Output: [[2,2,2],[2,2,0],[2,0,1]]
Explanation:
From the center of the image (with position (sr, sc) = (1, 1)), all pixels connected
by a path of the same color as the starting pixel are colored with the new color.
Note the bottom corner is not colored 2, because it is not 4-directionally connected
to the starting pixel.

Note:

  • The length of image and image[0] will be in the range [1, 50].

  • The given starting pixel will satisfy 0 <= sr < image.length and 0 <= sc < image[0].length.

  • The value of each color in image[i][j] and newColor will be an integer in [0, 65535].

Hint 1:

Write a recursive function that paints the pixel if it’s the correct color, then recurses on neighboring pixels.

Explanation 1

  1. Similar to [LeetCode] 200. Number of Islands, we can use DFS to solve this problem. First, we need to record the source pixel’s color as sColor. Then fill the source pixel with newColor, and recursively flood fill its 4 neighbors.

  2. The base case is if the current source is out of bound, we return; or the current source pixel’s color is not the same as sColor, we return; or the current source pixel’s color is the same as newColor, we return.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
    dfs(image, sr, sc, newColor, image[sr][sc])
    return image
}

func dfs(image [][]int, sr, sc, newColor, sColor int) {
    if sr < 0 || sr >= len(image) || sc < 0 || sc >= len(image[0]) ||
        image[sr][sc] != sColor || image[sr][sc] == newColor {
        return
    }

    image[sr][sc] = newColor

    dr := []int{-1, 0, 0, 1}
    dc := []int{0, -1, 1, 0}
    for i := 0; i < 4; i++ {
        dfs(image, sr + dr[i], sc + dc[i], newColor, sColor)
    }
}

Explanation 2

  1. We can also use BFS to solve this problem.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
    sColor := image[sr][sc]
    if sColor == newColor { return image }

    row, col := len(image), len(image[0])
    queue := make([]int, 0)
    queue = append(queue, sr * col + sc)

    for len(queue) > 0 {
        pollNum := queue[0]
        queue = queue[1:]
        curRow, curCol := pollNum / col, pollNum % col
        if image[curRow][curCol] != sColor || image[curRow][curCol] == newColor {
            continue
        }
        image[curRow][curCol] = newColor
        if curRow - 1 >= 0 { queue = append(queue, (curRow-1) * col + curCol) }
        if curRow + 1 < row { queue = append(queue, (curRow+1) * col + curCol) }
        if curCol - 1 >= 0 { queue = append(queue, curRow * col + curCol - 1) }
        if curCol + 1 < col { queue = append(queue, curRow * col + curCol + 1) }
    }
    return image
}

Single Element in a Sorted Array

You are given a sorted array consisting of only integers where every element appears exactly twice, except for one element which appears exactly once. Find this single element that appears only once.

Example 1:

1
2
Input: [1,1,2,3,3,4,4,8,8]
Output: 2

Example 2:

1
2
Input: [3,3,7,7,10,11,11]
Output: 10

Note: Your solution should run in O(log n) time and O(1) space.

Explanation

  1. Since it’s O(log n) runtime, we should use binary search to solve this problem.

  2. If all elements appear twice in the array, then this array will be index0 and index1 is a pair that have the same value, index2 and index 3 is a pair that have the same value, index4 and index5 is a pair that have the same value, etc. For example [1, 1, 2, 2]. Now, there’s one element add into the array. We have [0, 1, 1, 2, 2], or [1, 1, 2, 2, 3]. And the pair relationship is changed.

  3. If input is [0, 1, 1, 2, 2], we see the middle pair [1, 2] relationship is not match, that means the added element is on the left side. If input is [1, 1, 2, 2, 3], we see the middle pair [2, 2] relationship match, that means the added element is on the right side.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func singleNonDuplicate(nums []int) int {
    left, right := 0, len(nums) - 1
    for left < right {
        mid := left + (right - left) >> 1
        if mid % 2 == 1 {
            mid -= 1
        }
        if nums[mid] == nums[mid + 1] {
            left = mid + 2
        } else {
            right = mid
        }
    }
    return nums[left]
}

Remove K Digits

Given a non-negative integer num represented as a string, remove k digits from the number so that the new number is the smallest possible.

Note:

  • The length of num is less than 10002 and will be ≥ k.

  • The given num does not contain any leading zero.

Example 1:

1
2
3
Input: num = "1432219", k = 3
Output: "1219"
Explanation: Remove the three digits 4, 3, and 2 to form the new number 1219 which is the smallest.

Example 2:

1
2
3
Input: num = "10200", k = 1
Output: "200"
Explanation: Remove the leading 1 and the number is 200. Note that the output must not contain leading zeroes.

Example 3:

1
2
3
Input: num = "10", k = 2
Output: "0"
Explanation: Remove all the digits from the number and it is left with nothing which is 0.

Explanation

  1. If the number is increasing, for example, num = 1234, then we remove from the right’s k numbers. If the number is out of order, for example num = 1324, and k = 1, then we should remove 3 and get 124. We remove 3 because 2 is less than its left side number.

  2. To solve this problem, think of using a stack, iterating every number and we want to push every number to the stack, but while the stack is not empty and the current number is less than the top number on the stack, then we pop the stack. Outside of this while loop, we push the current number on the stack. For example num = 1324, we push 1 on the stack [1], push 3 on the stack [1, 3], when current number is 2, because 2 < 3, we pop the stack and now stack is [1], we push 2 and get [1, 2], and next iteration, current number is 4, we push to stack [1, 2, 4]. What if later there are many bigger number? This doesn’t matter because those bigger numbers’ significant digit are lower than current number’s significant digit, we should lower the numbers that are in higher significant digit.

  3. We should consider leading zero case, if leading zero, we remove all leading zero. And when outside of the iteration, if k is still greater than 0, we should remove k numbers from the right.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func removeKdigits(num string, k int) string {
    st := make([]rune, 0)
    for _, ch := range num {
        for k > 0 && len(st) > 0 && st[len(st)-1] > ch {
            st = st[:len(st)-1]
            k -= 1
        }
        st = append(st, ch)
    }

    for len(st) > 0 && st[0] == '0' {
        st = st[1:]
    }
    if k > 0 && len(st) >= k {
        st = st[:len(st)-k]
    }
    if len(st) == 0 { return "0" }

    var res strings.Builder
    for _, ch := range st {
        res.WriteRune(ch)
    }
    return res.String()
}

Implement Trie (Prefix Tree)

Implement a trie with insert, search, and startsWith methods.

Example:

1
2
3
4
5
6
7
8
Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // returns true
trie.search("app");     // returns false
trie.startsWith("app"); // returns true
trie.insert("app");
trie.search("app");     // returns true

Note:

  • You may assume that all inputs are consist of lowercase letters a-z.

  • All inputs are guaranteed to be non-empty strings.

Explanation 1

  1. First, we need to think about what property the Trie pointer should have. Since all inputs are lowercase letters a-z, we can create an array Trie[] children[26] to store the inserted characters. For example, if children[0] != null, that means we have character a. Since we need to find out if the Trie contain all characters of the word, so we need property boolean isEnd to represent if this Trie pointer is the end of the word.

  2. In the constructor, we initialize children = new Trie[26] and isEnd = false.

  3. In the insert method, first we need to create a pointer cur to point to this Trie. Then loop through all characters of the word. If cur.children[ch - 'a'] is NULL, that means we haven’t inserted this current character ch before, so we insert it by creating a new Trie in its corresponding index. Then update the current pointer pointing to the character’s corresponding Triecur.children[ch - 'a']. Repeat this loop. After looping all characters, we mark the current Trie’s property isEnd to true.

  4. In the search method, we also need to create a pointer cur to this Trie first. Then loop through all characters of the word, If current Trie’s children doesn’t have this current character, we return false. In other word, if cur.children[ch - 'a'] is NULL, that means we don’t have the current character in this Trie. Else, we update the pointer cur to the corresponding character’s Trie. At the end, we return cur.isEnd to check if this character is the end of the word.

  5. In the startsWith method, simillar to the search method, we loop thorugh all characters and check if the children has this character. Except outside the loop, we return true instead of cur.isEnd.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
type Trie struct {
    children []*Trie
    isEnd bool
}


/** Initialize your data structure here. */
func Constructor() Trie {
    return Trie{make([]*Trie, 26), false}
}


/** Inserts a word into the trie. */
func (this *Trie) Insert(word string)  {
    cur := this
    for _, ch := range word {
        if cur.children[ch - 'a'] == nil {
            cur.children[ch - 'a'] = &Trie{make([]*Trie, 26), false}
        }
        cur = cur.children[ch - 'a']
    }
    cur.isEnd = true
}


/** Returns if the word is in the trie. */
func (this *Trie) Search(word string) bool {
    cur := this
    for _, ch := range word {
        if cur.children[ch - 'a'] == nil{
            return false
        }
        cur = cur.children[ch - 'a']
    }
    return cur.isEnd
}


/** Returns if there is any word in the trie that starts with the given prefix. */
func (this *Trie) StartsWith(prefix string) bool {
    cur := this
    for _, ch := range prefix {
        if cur.children[ch - 'a'] == nil {
            return false
        }
        cur = cur.children[ch - 'a']
    }
    return true
}


/**
 * Your Trie object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Insert(word);
 * param_2 := obj.Search(word);
 * param_3 := obj.StartsWith(prefix);
 */

Explanation 2

  1. We can also use property HashMap<Character, Trie> instead of array Trie[]. HashMap will save space if we have a lot of different characters.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
type Trie struct {
    Hm map[rune]*Trie
    IsEnd bool
}


/** Initialize your data structure here. */
func Constructor() Trie {
    return Trie{make(map[rune]*Trie), false}
}


/** Inserts a word into the trie. */
func (this *Trie) Insert(word string)  {
    cur := this
    for _, ch := range word {
        if _, ok := cur.Hm[ch]; !ok {
            cur.Hm[ch] = &Trie{make(map[rune]*Trie), false}
        }
        cur = cur.Hm[ch]
    }
    cur.IsEnd = true
}


/** Returns if the word is in the trie. */
func (this *Trie) Search(word string) bool {
    cur := this
    for _, ch := range word {
        if _, ok := cur.Hm[ch]; !ok {
            return false
        }
        cur = cur.Hm[ch]
    }
    return cur.IsEnd
}


/** Returns if there is any word in the trie that starts with the given prefix. */
func (this *Trie) StartsWith(prefix string) bool {
    cur := this
    for _, ch := range prefix {
        if _, ok := cur.Hm[ch]; !ok {
            return false
        }
        cur = cur.Hm[ch]
    }
    return true
}


/**
 * Your Trie object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Insert(word);
 * param_2 := obj.Search(word);
 * param_3 := obj.StartsWith(prefix);
 */

Week 3: May 15th–May 21st

Maximum Sum Circular Subarray

Given a circular array C of integers represented by A, find the maximum possible sum of a non-empty subarray of C.

Here, a circular array means the end of the array connects to the beginning of the array. (Formally, C[i] = A[i] when 0 <= i < A.length, and C[i+A.length] = C[i] when i >= 0.)

Also, a subarray may only include each element of the fixed buffer A at most once. (Formally, for a subarray C[i], C[i+1], ..., C[j], there does not exist i <= k1, k2 <= j with k1 % A.length = k2 % A.length.)

Example 1:

1
2
3
Input: [1,-2,3,-2]
Output: 3
Explanation: Subarray [3] has maximum sum 3

Example 2:

1
2
3
Input: [5,-3,5]
Output: 10
Explanation: Subarray [5,5] has maximum sum 5 + 5 = 10

Example 3:

1
2
3
Input: [3,-1,2,-1]
Output: 4
Explanation: Subarray [2,-1,3] has maximum sum 2 + (-1) + 3 = 4

Example 4:

1
2
3
Input: [3,-2,2,-3]
Output: 3
Explanation: Subarray [3] and [3,-2,2] both have maximum sum 3

Example 5:

1
2
3
Input: [-2,-3,-1]
Output: -1
Explanation: Subarray [-1] has maximum sum -1

Note:

  1. -30000 <= A[i] <= 30000

  2. 1 <= A.length <= 30000

Hint 1:

For those of you who are familiar with the Kadane’s algorithm, think in terms of that. For the newbies, Kadane’s algorithm is used to finding the maximum sum subarray from a given array. This problem is a twist on that idea and it is advisable to read up on that algorithm first before starting this problem. Unless you already have a great algorithm brewing up in your mind in which case, go right ahead!

Hint 2:

What is an alternate way of representing a circular array so that it appears to be a straight array? Essentially, there are two cases of this problem that we need to take care of. Let’s look at the figure below to understand those two cases:

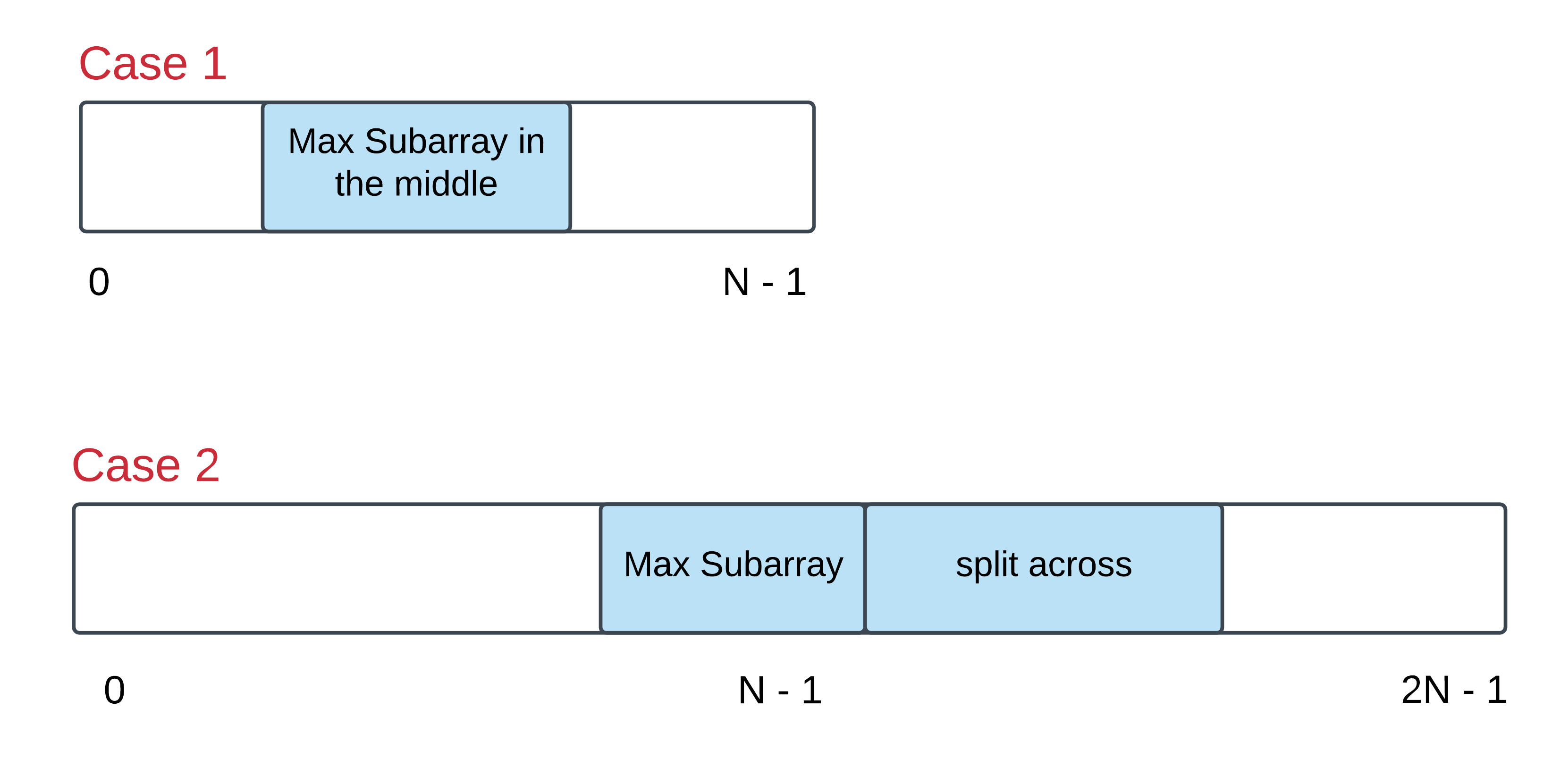
Maximum Sum Circular Subarray

Hint 3:

The first case can be handled by the good old Kadane’s algorithm. However, is there a smarter way of going about handling the second case as well?

Explanation

  1. If the array is not circular, then this problem is the same as 53. Maximum Subarray, we can use Kadane’s algorithm to find out the maximum sum of the subarray. In Kadane’s algorithm, we loop through the array, for each index, we think of it as the ending index of the subarray and we calculate its maximum sum that ends at that index. For example, if the current index is i, then the maximum sum ending at index i is max(nums[i], nums[i] + maxSumEndAt(i-1)).

  2. Now in this problem, the subarray can be circular. We need to consider two cases. First case is the maximum subarray is not circular. For example, [1, -2, 3, 4, -1, 5, -3, -1]. The maximum subarray is [3, 4, -1, 5]. We can find out the maximum sum subarray using Kadane’s algorithm.

  3. The second case is the maximum sum subarray is circular. For example, in [5, -3, 1, -7, 2], the maximum sum subarray will be [2, 5] that is formed by the first number and the last number. We notice that other numbers in the middle [-3, 1, -7] is the Minimum Sum Subarray, also [2, 5] + [-3, 1, -7] is the total sum of the input array. In this case the MaxSumSubArray = totalSum - MinSumSubArray. We can actually use Kadane’s algorithm to find out the MinSumSubArray, then we use the total sum to subtract it to get the maximum sum subarray.

  4. After considering these two cases, we can loop through the input array, calculate the totalSum, MaxSumSubArray and MinSumSubArray. At the end we return max(MaxSumSubArray, total - MinSumSubArray).

  5. There’s also an edge case. If all numbers are negative in the input array, in other word, the MaxSumSubArray is negative, then we return MaxSumSubArray.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func maxSubarraySumCircular(A []int) int {
    total := 0
    globalMax := math.MinInt32
    localMax := 0
    globalMin := math.MaxInt32
    localMin := 0

    for _, num := range A {
        total += num
        localMax = max(localMax + num, num)
        globalMax = max(globalMax, localMax)
        localMin = min(localMin + num, num)
        globalMin = min(globalMin, localMin)
    }

    if globalMax < 0 {
        return globalMax
    } else {
        return max(globalMax, total - globalMin)
    }
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Odd Even Linked List

Given a singly linked list, group all odd nodes together followed by the even nodes. Please note here we are talking about the node number and not the value in the nodes.

You should try to do it in place. The program should run in O(1) space complexity and O(nodes) time complexity.

Example 1:

1
2
Input: 1->2->3->4->5->NULL
Output: 1->3->5->2->4->NULL

Example 2:

1
2
Input: 2->1->3->5->6->4->7->NULL
Output: 2->3->6->7->1->5->4->NULL

Note:

  • The relative order inside both the even and odd groups should remain as it was in the input.

  • The first node is considered odd, the second node even and so on …

Explanation

  1. We can also first create an odd pointer points to the first node, even pointer points to the second node. Then we create a evenHead pointer poions to the second node also.

  2. We make odd pointer’s next node points at even.next, which is always odd, then odd pointer move one step forward. Then we make even pointer’s next node points at odd.next which is alwasy even, then even pointer move one step forward. Repeat until even.next is NULL.

  3. We connect odd.next to evenHead.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func oddEvenList(head *ListNode) *ListNode {
    if head == nil || head.Next == nil { return head }
    odd := head
    even := head.Next
    oddHead := odd
    evenHead := even

    for odd != nil && even != nil && even.Next != nil {
        odd.Next = even.Next
        odd = odd.Next
        even.Next = odd.Next
        even = even.Next
    }

    odd.Next = evenHead
    return oddHead
}

Find All Anagrams in a String

Given a string s and a non-empty string p, find all the start indices of p’s anagrams in s.

Strings consists of lowercase English letters only and the length of both strings s and p will not be larger than 20,100.

The order of output does not matter.

Example 1:

1
2
3
4
5
6
7
8
9
Input:
s: "cbaebabacd" p: "abc"

Output:
[0, 6]

Explanation:
The substring with start index = 0 is "cba", which is an anagram of "abc".
The substring with start index = 6 is "bac", which is an anagram of "abc".

Example 2:

1
2
3
4
5
6
7
8
9
10
Input:
s: "abab" p: "ab"

Output:
[0, 1, 2]

Explanation:
The substring with start index = 0 is "ab", which is an anagram of "ab".
The substring with start index = 1 is "ba", which is an anagram of "ab".
The substring with start index = 2 is "ab", which is an anagram of "ab".

Explanation 1

  1. I think this solution is easier to understand. First, we add all p’s characters in an array pFreq[] to record the frequency of p’s characters, and it has length 26. For example, if pFreq[0] = 2 then it means a’s frequency is 2; if pFreq[1] = 0 then means b’s frequency is 0.

  2. Initialize start is 0, and loop through the first group or len(p) characters in s. In each iteration, we decrease the corresponding character’s frequency by 1 in pFreq[]. For example, if p = "abc", then pFreq = {1, 1, 1}. If we have s = "aabc", then we check the first group’s characters aab and subtract pFreq’s corresponding character frequency, we get pFreq = {-1, 0, 1}.

  3. Initialize misMatch = false, and loop through pFreq[]. If any frequency is not 0, that means the current group is mismatch, so we update misMatch = true and break out this loop. After this loop, if misMatch is still false, then we add start to the result list.

  4. Now, we finish checking the first group’s character in s, we can increase start by 1. Now, we remove the most left character a and update its corresponding frequency in pFreq[start - 1] += 1. Also we add the new character c into the current group and update pFreq[start + len(p) - 1] -= 1. Then, we repeat the last step checking if all characters in pFreq[] have frequency 0. If true, then we update misMatch to false and add start into the result list. After checking, we increase start by 1 and repeat this step while start <= len(s) - len(p).

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
func findAnagrams(s string, p string) []int {
    res := make([]int, 0)
    if len(p) > len(s) { return res }

    pFreq := make([]int, 26)
    for _, ch := range p {
        pFreq[ch - 'a'] += 1
    }

    start := 0
    for i := 0; i < len(p); i++ {
        pFreq[s[i] - 'a'] -= 1
    }

    misMatch := false
    for _, freq := range pFreq {
        if freq != 0 {
            misMatch = true
            break
        }
    }

    if misMatch == false { res = append(res, start) }

    start += 1

    for start <= len(s) - len(p) {
        idx1 := s[start - 1]
        idx2 := s[start + len(p) - 1]
        pFreq[idx1 - 'a'] += 1
        pFreq[idx2 - 'a'] -= 1

        misMatch = false
        for _, freq := range pFreq {
            if freq != 0 {
                misMatch = true
                break
            }
        }

        if misMatch == false { res = append(res, start) }

        start += 1
    }

    return res
}

Explanation 2

  1. We can improve the last solution by counting how many miss-match characters instead of checking miss-match true of false.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
func findAnagrams(s string, p string) []int {
    res := make([]int, 0)
    if len(p) > len(s) { return res }

    pFreq := make([]int, 26)
    for _, ch := range p {
        pFreq[ch - 'a'] += 1
    }

    start := 0
    for i := 0; i < len(p); i++ {
        pFreq[s[i] - 'a'] -= 1
    }

    misMatchCnt := 0
    for _, freq := range pFreq {
        if freq != 0 {
            misMatchCnt += 1
        }
    }

    if misMatchCnt == 0 { res = append(res, start) }

    start += 1

    for start <= len(s) - len(p) {
        idx1 := s[start - 1]
        idx2 := s[start + len(p) - 1]

        pFreq[idx1 - 'a'] += 1
        if pFreq[idx1 - 'a'] == 0 {
            misMatchCnt -= 1
        } else if pFreq[idx1 - 'a'] == 1 {
            misMatchCnt += 1
        }

        pFreq[idx2 - 'a'] -= 1
        if pFreq[idx2 - 'a'] == 0 {
            misMatchCnt -= 1
        } else if pFreq[idx2 - 'a'] == -1 {
            misMatchCnt += 1
        }

        if misMatchCnt == 0 { res = append(res, start) }

        start += 1
    }

    return res
}

Permutation in String

Given two strings s1 and s2, write a function to return true if s2 contains the permutation of s1. In other words, one of the first string’s permutations is the substring of the second string.

Example 1:

1
2
3
Input: s1 = "ab" s2 = "eidbaooo"
Output: True
Explanation: s2 contains one permutation of s1 ("ba").

Example 2:

1
2
Input:s1= "ab" s2 = "eidboaoo"
Output: False

Note:

  1. The input strings only contain lower case letters.

  2. The length of both given strings is in range [1, 10,000].

Hint 1:

Obviously, brute force will result in TLE. Think of something else.

Hint 2:

How will you check whether one string is a permutation of another string?

Hint 3:

One way is to sort the string and then compare. But, Is there a better way?

Hint 4:

If one string is a permutation of another string then they must one common metric. What is that?

Hint 5:

Both strings must have same character frequencies, if one is permutation of another. Which data structure should be used to store frequencies?

Hint 6:

What about hash table? An array of size 26?

Explanation

  1. In Find All Anagrams in a String, we are finding a list of starting indexes of anagrams in a string. Note, anagrams is the same as permutation. In this problem, we can use its solution to return a list of of starting indexes of permutation of s1 in s2. If this list is empty, that means there’s no permutation of s1 in s2, so we return false. Else, we return true. Or, if the misMatchCnt is 0, we can return true immediately.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
func checkInclusion(s1 string, s2 string) bool {
    if len(s1) > len(s2) { return false }
    s1Freq := make([]int, 26)
    for _, ch := range s1 {
        s1Freq[ch - 'a'] += 1
    }

    for i := 0; i < len(s1); i++ {
        s1Freq[s2[i] - 'a'] -= 1
    }

    start := 0
    misMatchCnt := 0

    for i := 0; i < len(s1Freq); i++ {
        if s1Freq[i] != 0 {
            misMatchCnt += 1
        }
    }

    if misMatchCnt == 0 { return true }
    start += 1

    for start <= len(s2) - len(s1) {
        idx1 := s2[start-1] - 'a'
        s1Freq[idx1] += 1
        if s1Freq[idx1] == 0 {
            misMatchCnt -= 1
        } else if s1Freq[idx1] == 1 {
            misMatchCnt += 1;
        }

        idx2 := s2[start + len(s1) - 1] - 'a'
        s1Freq[idx2] -= 1
        if s1Freq[idx2] == 0 {
            misMatchCnt -= 1
        } else if s1Freq[idx2] == -1 {
            misMatchCnt += 1
        }

        if misMatchCnt == 0 { return true }
        start += 1
    }

    return false
}

Online Stock Span

Write a class StockSpanner which collects daily price quotes for some stock, and returns the span of that stock’s price for the current day.

The span of the stock’s price today is defined as the maximum number of consecutive days (starting from today and going backwards) for which the price of the stock was less than or equal to today’s price.

For example, if the price of a stock over the next 7 days were [100, 80, 60, 70, 60, 75, 85], then the stock spans would be [1, 1, 1, 2, 1, 4, 6].

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input: ["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
Output: [null,1,1,1,2,1,4,6]
Explanation:
First, S = StockSpanner() is initialized.  Then:
S.next(100) is called and returns 1,
S.next(80) is called and returns 1,
S.next(60) is called and returns 1,
S.next(70) is called and returns 2,
S.next(60) is called and returns 1,
S.next(75) is called and returns 4,
S.next(85) is called and returns 6.

Note that (for example) S.next(75) returned 4, because the last 4 prices
(including today's price of 75) were less than or equal to today's price.

Note:

Calls to StockSpanner.next(int price) will have 1 <= price <= 10^5. There will be at most 10000 calls to StockSpanner.next per test case. There will be at most 150000 calls to StockSpanner.next across all test cases. The total time limit for this problem has been reduced by 75% for C++, and 50% for all other languages.

Explanation 1

  1. In the constructor method we create two lists prices and spans. In the next method, we are adding a new price and we need to find the current price’s span.

  2. We can compare current price with the its previous price, if the previous price is greater, then we add the current price to the list prices, and current price’s span is 1 and add to the spans list.

  3. Else if the previous price is smaller, then previous price’s span will also be part of the current price’s span. From the problem’s example, if current price is 85, its previous price is 75, previous price’s span is 4, then we update the new previous price be previousPriceIdx = previousPriceIdx - 4 which now points to price 80 at index 1. Repeat this step, we compare current price 85 with the new previous price 80. Since current price is greater and previous price’s span is 1, we update newPreviousPrice = newPreviousPrice - 1. Now previous price is 100 which is greater than current price 85, we stop here. Now, we can calculate current price’s span is current price’s index minus previous price’s index. In this case, current price 85’s span is 6 - 0 = 6.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
type StockSpanner struct {
    prices []int
    spans []int
}


func Constructor() StockSpanner {
    return StockSpanner{make([]int, 0), make([]int, 0)}
}


func (this *StockSpanner) Next(price int) int {
    prevPriceIdx := len(this.prices) - 1
    currPriceIdx := len(this.prices)

    for prevPriceIdx >= 0 && this.prices[prevPriceIdx] <= price {
        prevPriceIdx -= this.spans[prevPriceIdx]
    }

    span := currPriceIdx - prevPriceIdx
    this.spans = append(this.spans, span)
    this.prices = append(this.prices, price)

    return span
}


/**
 * Your StockSpanner object will be instantiated and called as such:
 * obj := Constructor();
 * param_1 := obj.Next(price);
 */

Explanation 2

  1. We can also use stack of a pair<price, span> to solve this problem. In the next method, we initialize current price’s span is 1. While current price is greater than the top stack’s price, we update span = span + st.top().second and pop the stack. Outside this while loop, we add current price and the updated span to the stack, and return the updated span.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
type StockSpanner struct {
    st [][2]int
}


func Constructor() StockSpanner {
    return StockSpanner{make([][2]int, 0)}
}


func (this *StockSpanner) Next(price int) int {
    span := 1

    for len(this.st) > 0 && this.st[len(this.st)-1][0] <= price {
        span += this.st[len(this.st)-1][1]
        this.st = this.st[:len(this.st)-1]
    }

    this.st = append(this.st, [2]int{price, span})

    return span
}


/**
 * Your StockSpanner object will be instantiated and called as such:
 * obj := Constructor();
 * param_1 := obj.Next(price);
 */

Kth Smallest Element in a BST

Given a binary search tree, write a function kthSmallest to find the kth smallest element in it.

Note:

You may assume k is always valid, 1 ≤ k ≤ BST’s total elements.

Example 1:

1
2
3
4
5
6
7
Input: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
Output: 1

Example 2:

1
2
3
4
5
6
7
8
9
Input: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
Output: 3

Follow up:

What if the BST is modified (insert/delete operations) often and you need to find the kth smallest frequently? How would you optimize the kthSmallest routine?

Hint 1:

Try to utilize the property of a BST.

Hint 2:

Try in-order traversal. (Credits to @chan13)

Hint 3:

What if you could modify the BST node’s structure?

Hint 4:

The optimal runtime complexity is O(height of BST).

Explanation 1

  1. We can use in-order traversal to solve this problem. In a recrusive way, we can first create a list to store all the elements that are traversaled and pass it to the recursive function. If the list has size k or the node is null, then we return out of the recursive function. In the main function, we can check if the list has size k, if it does, then return the k element in the list, else return -1.

  2. Instead of storing an element into a list each time, we can also increment a counter. When the counter is equal to k, we store the element’s value into the result variable and return the result at the end.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func kthSmallest(root *TreeNode, k int) int {
    res := 0
    cnt := 0
    inOrder(root, k, &res, &cnt)
    return res
}

func inOrder(root *TreeNode, k int, res, cnt *int) {
    if root == nil { return }
    inOrder(root.Left, k, res, cnt)
    *cnt += 1
    if *cnt == k {
        *res = root.Val
        return;
    }
    inOrder(root.Right, k, res, cnt)
}

Explanation 2

  1. We want to find the kth smallest element. First, count how many nodes in the left subtree. If there are cnt nodes in the left subtree, including root.left, and cnt >= k. Then, we recursivly call the main method with parameter (root.left, k). If k > cnt+1, then the kth node is in the right subtree; we plus one because that one is the root node. If cnt doesn’t satisfy the above two conditions, then return root.val as the result.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func kthSmallest(root *TreeNode, k int) int {
    cnt := count(root.Left)
    if cnt >= k {
        return kthSmallest(root.Left, k)
    } else if cnt + 1 < k {
        return kthSmallest(root.Right, k - (cnt + 1))
    } else {
        return root.Val
    }
}

func count(root *TreeNode) int {
    if root == nil { return 0 }
    return 1 + count(root.Left) + count(root.Right)
}

Explanation 3

  1. For the follow up question, we find the kth smallest frequently, we can use the above method of comparing the counter. But it takes a lot of time if we recursivly calculate every node’s counter. So, we can change the TreeNode data structure to create a MyTreeNode data structure to include a counter for every node. So first, we need to build a tree of MyTreeNode.

  2. After we build a tree of MyTreeNode we get the myRoot. Then, we create a helper function similar to the above solution, comparing the counter and k. In the helper function, we first check if there is a root.left, if yes, then similar to the above solutioin. Else, check if k is 1, if k=1, then we return the root node, otherwise, we check the right child node with parameter root.right and k-1.

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
type MyTreeNode struct {
    Val int
    Left *MyTreeNode
    Right *MyTreeNode
    Count int
}

func Constructor(val int) *MyTreeNode {
    return &MyTreeNode{Val: val, Count: 1}
}

func kthSmallest(root *TreeNode, k int) int {
    myRoot := build(root)
    return helper(myRoot, k)
}

func build(root *TreeNode) *MyTreeNode {
    if root == nil { return nil }
    myRoot := Constructor(root.Val)
    myRoot.Left = build(root.Left)
    myRoot.Right = build(root.Right)

    if myRoot.Left != nil {
        myRoot.Count += myRoot.Left.Count
    }
    if myRoot.Right != nil {
        myRoot.Count += myRoot.Right.Count
    }
    return myRoot
}

func helper(root *MyTreeNode, k int) int {
    if root.Left != nil {
        if root.Left.Count >= k {
            return helper(root.Left, k)
        } else if root.Left.Count + 1 < k {
            return helper(root.Right, k - (root.Left.Count + 1))
        } else {
            return root.Val
        }
    } else {
        if k == 1 { return root.Val }
        return helper(root.Right, k - 1)
    }
}

Count Square Submatrices with All Ones

Given a m * n matrix of ones and zeros, return how many square submatrices have all ones.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input: matrix =
[
  [0,1,1,1],
  [1,1,1,1],
  [0,1,1,1]
]
Output: 15

Explanation:
There are 10 squares of side 1.
There are 4 squares of side 2.
There is  1 square of side 3.
Total number of squares = 10 + 4 + 1 = 15.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
Input: matrix =
[
  [1,0,1],
  [1,1,0],
  [1,1,0]
]
Output: 7
Explanation:
There are 6 squares of side 1.
There is 1 square of side 2.
Total number of squares = 6 + 1 = 7.

Constraints:

  • 1 <= arr.length <= 300

  • 1 <= arr[0].length <= 300

  • 0 <= arr[i][j] <= 1

Hint 1:

Create an additive table that counts the sum of elements of submatrix with the superior corner at (0,0).

Hint 2:

Loop over all subsquares in O(n^3) and check if the sum make the whole array to be ones, if it checks then add 1 to the answer.

Explanation

  1. Similar to 221. Maximal Square, now we are finding the number of squares instead of the maximal square. We know that if the bottom right of the square is fixed, then we have if the maximum side of the square is 1, then there is 1 square; if the maximum side of the square is 2, then there are 2 squares have the same bottom right; if the maximum side of the square is 3, then there are 3 squares have the same bottom right. So we need to iterate over the matrix and sum up each square’s maximum side.

  2. We can create another matrix dp that have the same size as the input matrix. In this new matrix, each element is used to represent the number of maximum side of the square which bottom right square is the current square. In the top row or left column, the maximum side of each square is the same as matrix[r][c]. Else, if the current matrix square is 0, then number of maximum side square’s bottom right at this current square is dp[r][c] = 0. If the current matrix square is not 0, then we need to consider its top square’s maximum side dp[r-1][c], its left square’s maximum side dp[r][c-1] and its topLeft square’s maximum side dp[r-1][c-1], and we take the minimum among these 3 squares plus 1, and the sum will be the current square’s maximum side.

  3. Since we only consider top, left, and topLeft, we can save sapce by creating an array dp that have same size as the column of the input matrix. Now current element dp[c]’s top is equal to dp[oldC], left is dp[c-1]. In order to have topLeft for the current square, in the previous iteration, we update topLeft = dp[prevOldC]. Also, initially, topLeft = matrix[0][0], and if current square’s column is at col - 1, then we update topLeft = dp[0].

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
func countSquares(matrix [][]int) int {
    row, col := len(matrix), len(matrix[0])
    dp := make([]int, col)
    res := 0
    topLeft := matrix[0][0]

    for r := 0; r < row; r++ {
        for c := 0; c < col; c++ {
            if r == 0 || c == 0 {
                dp[c] = matrix[r][c];
                res += dp[c];
            } else {
                temp := dp[c];

                if matrix[r][c] != 0 {
                    dp[c] = min(topLeft, min(dp[c], dp[c-1])) + 1;
                } else {
                    dp[c] = 0;
                }
                res += dp[c];

                if c == col - 1 {
                    topLeft = dp[0]
                } else {
                    topLeft = temp
                }
            }
        }
    }

    return res;
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Week 4: May 22nd–May 28th

Sort Characters By Frequency

Given a string, sort it in decreasing order based on the frequency of characters.

Example 1:

1
2
3
4
5
6
7
8
9
Input:
"tree"

Output:
"eert"

Explanation:
'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr" is also a valid answer.

Example 2:

1
2
3
4
5
6
7
8
9
Input:
"cccaaa"

Output:
"cccaaa"

Explanation:
Both 'c' and 'a' appear three times, so "aaaccc" is also a valid answer.
Note that "cacaca" is incorrect, as the same characters must be together.

Example 3:

1
2
3
4
5
6
7
8
9
Input:
"Aabb"

Output:
"bbAa"

Explanation:
"bbaA" is also a valid answer, but "Aabb" is incorrect.
Note that 'A' and 'a' are treated as two different characters.

Explanation 1

  1. First, we need to use a HashMap to count all characters’ frequency. Then, we use a PriorityQueue or List to store the HashMap’s entry pair. Then, sort it by frequency descending. Next, we iterate the sorted PriorityQueue or List and store the entry key by the number of entry value times to the result string.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func frequencySort(s string) string {
    hm := make(map[rune]int)
    for _, ch := range s {
        hm[ch]++
    }

    lst := make([]pair, 0)
    for ch, freq := range hm {
        lst = append(lst, pair{ch, freq})
    }
    sort.Slice(lst, func(i, j int) bool {
        return lst[i].Freq > lst[j].Freq
    })

    res := strings.Builder{}
    for _, p := range lst {
        for i := 0; i < p.Freq; i++ {
            res.WriteRune(p.Ch)
        }
    }

    return res.String()
}

type pair struct {
    Ch rune
    Freq int
}

Explanation 2

  1. We can also use bucket sort to solve this problem. First, we store the character and its frequency to a HashMap. Next, we create an array of list. Iterate the HashMap, for each entry, its frequency will be the array’s index, its key, in other words, the character will be added to the list on that index.

  2. Next, we iterate the array from right to left, if the element on the current index is null, that means there’s no list, so we continue. Else, the current index has a list, then we append the list’s character the number of index times to the StringBuilder.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func frequencySort(s string) string {
    hm := make(map[rune]int)
    maxFreq := 0
    for _, ch := range s {
        hm[ch]++
        maxFreq = max(maxFreq, hm[ch])
    }

    arr := make([][]rune, maxFreq + 1)

    for ch, freq := range hm {
        arr[freq] = append(arr[freq], ch)
    }

    res := strings.Builder{}
    for freq := len(arr) - 1; freq >= 0; freq-- {
        if len(arr[freq]) == 0 { continue }

        for _, ch := range arr[freq] {
            for i := 0; i < freq; i++ {
                res.WriteRune(ch)
            }
        }
    }

    return res.String()
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Interval List Intersections

Given two lists of closed intervals, each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

(Formally, a closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b. The intersection of two closed intervals is a set of real numbers that is either empty, or can be represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].)

Example 1:

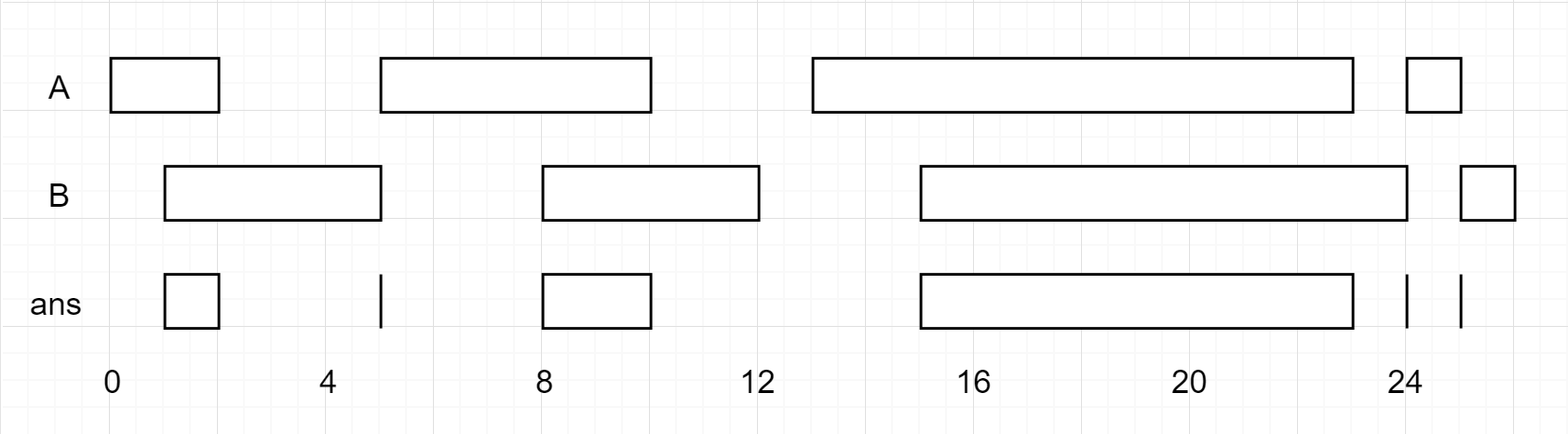
Interval List Intersections

1
2
3
Input: A = [[0,2],[5,10],[13,23],[24,25]], B = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
Reminder: The inputs and the desired output are lists of Interval objects, and not arrays or lists.

Note:

  1. 0 <= A.length < 1000

  2. 0 <= B.length < 1000

  3. 0 <= A[i].start, A[i].end, B[i].start, B[i].end < 10^9

NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

Explanation

  1. If two intervals a and b are overlapped, we can get the intersection by intersection = {max(a[0], b[0]), min(a[1], b[1]) }.

  2. We use i and j to denote the index of the current intervals of A and B respectively. While i < len(A) && j < len(B), then we keep comparing A[i] and B[j].

  3. Let’s use variable a and b to denote the current interval A[i] and B[j] respectively. There are only two cases when a and b are not overlapped. The first case is a[1] < b[0], the second case is b[1] < a[0]. If a[1] < b[0], then we increase i. If b[1] < a[0], then we increase j.

  4. If a and b are overlapped, then we calculate their intersection and add to the result list, and increase the index of the interval that’s ending earlier. Repeat these steps until outside the while loop.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func intervalIntersection(A [][]int, B [][]int) [][]int {
    res := make([][]int, 0)
    i := 0
    j := 0
    for i < len(A) && j < len(B) {
        a := A[i]
        b := B[j]
        if a[1] < b[0] {
            i += 1
        } else if b[1] < a[0] {
            j += 1
        } else {
            start := max(a[0], b[0])
            end := min(a[1], b[1])
            res = append(res, []int{start, end})
            if (a[1] < b[1]) {
                i += 1
            } else if (b[1] < a[1]) {
                j += 1
            } else if (a[1] == b[1]) {
                i += 1
                j += 1
            }
        }
    }

    return res
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Construct Binary Search Tree from Preorder Traversal

Return the root node of a binary search tree that matches the given preorder traversal.

(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)

Example 1:

1
2
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]

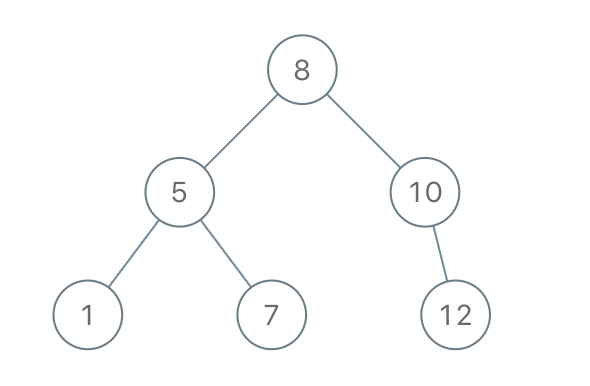
1008. Construct Binary Search Tree from Preorder Traversal

Constraints:

  1. 1 <= preorder.length <= 100

  2. 1 <= preorder[i] <= 10^8

  3. The values of preorder are distinct.

Explanation 1

  1. Since the input array is preorder traversal, so the first element is the root. From the problem’s example, 8 will be the root. How do we knowroot.left and root.right? root.left = 5 because 5 is the next element of 8, and 5 is less than 8. To find root.right, we need to loop from the second element to the right until the current element is greater than the root, which is 10 from the above example.

  2. Now we know [5, 1, 7] will be in the left subtree, [10, 12] will be in the right subtree. We can create a helper method, pass the input array, and two variables start and end which represent the range of the subarray. This helper method will recursively create the binary search tree for the left subtree and right subtree.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstFromPreorder(preorder []int) *TreeNode {
    if preorder == nil || len(preorder) == 0 { return nil }
    return helper(preorder, 0 , len(preorder)-1)
}

func helper(preorder []int, start int, end int) *TreeNode {
    if start > end { return nil }
    root := &TreeNode{ Val: preorder[start] }
    if start == end { return root }
    i := start + 1
    for i <= end && preorder[i] < preorder[start] {
        i += 1
    }
    root.Left = helper(preorder, start+1, i-1)
    root.Right = helper(preorder, i, end)
    return root
}

Explanation 2

  1. We can also solve this problem in $O(n)$ runtime by using a global index i to represent the current index of the input array. Reading the problem, 5 is the left child or 8, 1 is the left child of 5, …, 7 cannot be the left child of 1 since 7 > 1, and 7 cannot be the right child of 1 since 7 > 5, but 7 can be the right child of 5 since 7 < 8.

  2. We can create a helper method, pass in the input array and the upper bound variablebound which initialize to INT_MAX. In the helper method, we create the root node, root.left will have the upper bound of root.val, and root.right will have the upper bound of bound. The base case is if i == len(preorder) or preorder[i] > bound, then we return NULL.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func bstFromPreorder(preorder []int) *TreeNode {
    if preorder == nil || len(preorder) == 0 { return nil }
    i := 0
    return helper(preorder, math.MaxInt32, &i)
}

func helper(preorder []int, bound int, i *int) *TreeNode {
    if *i == len(preorder) || preorder[*i] > bound { return nil }
    root := &TreeNode{Val: preorder[*i]}
    *i += 1
    root.Left = helper(preorder, root.Val, i)
    root.Right = helper(preorder, bound, i)
    return root
}

Uncrossed Lines

We write the integers of A and B (in the order they are given) on two separate horizontal lines.

Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that:

  • A[i] == B[j];

  • The line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line.

Return the maximum number of connecting lines we can draw in this way.

Example 1:

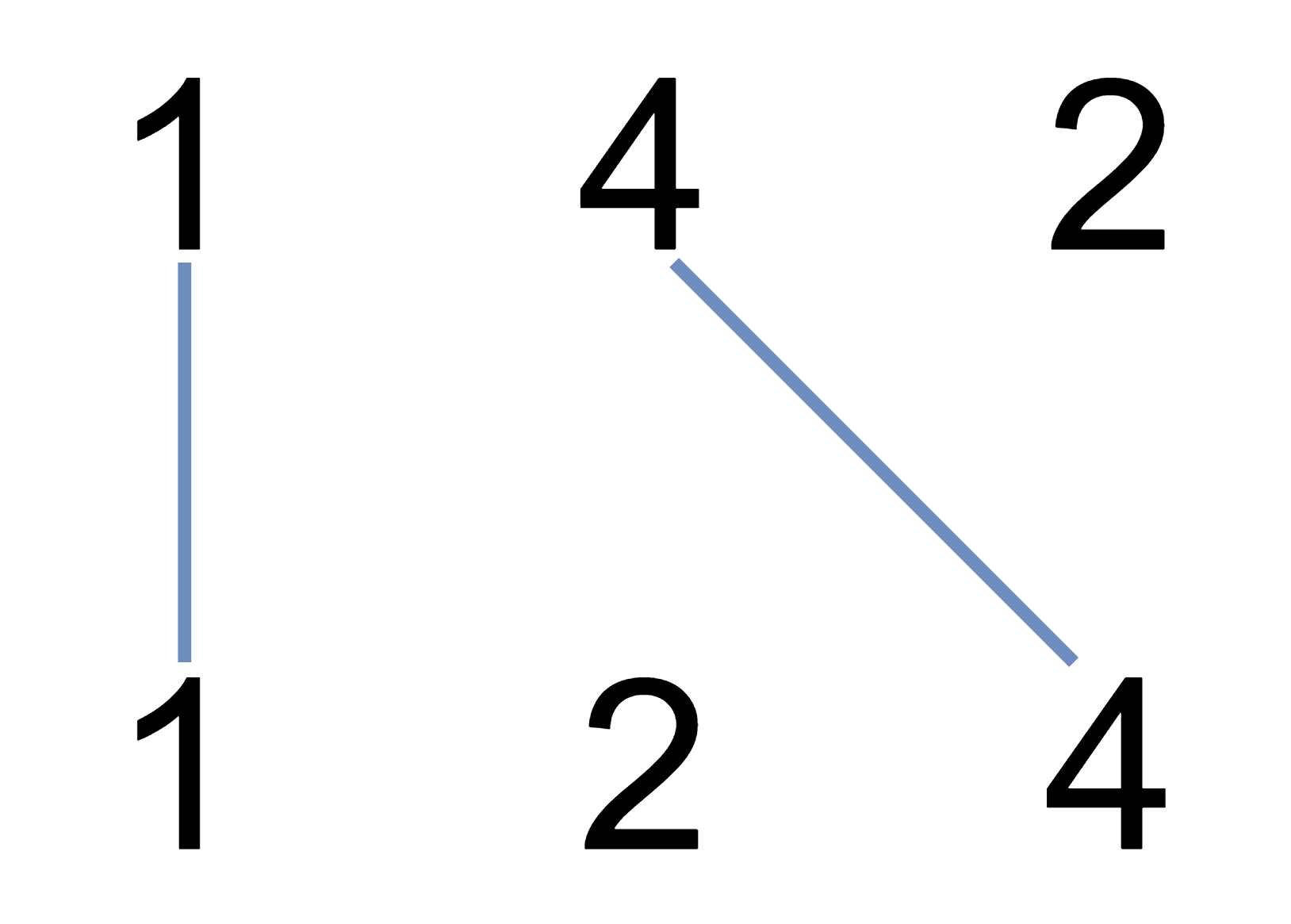
Uncrossed Lines

1
2
3
4
Input: A = [1,4,2], B = [1,2,4]
Output: 2
Explanation: We can draw 2 uncrossed lines as in the diagram.
We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2.

Example 2:

1
2
Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2]
Output: 3

Example 3:

1
2
Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1]
Output: 2

Note:

  1. 1 <= A.length <= 500

  2. 1 <= B.length <= 500

  3. 1 <= A[i], B[i] <= 2000

Hint 1:

Think dynamic programming. Given an oracle dp(i,j) that tells us how many lines A[i:], B[j:] [the sequence A[i], A[i+1], … and B[j], B[j+1], …] are uncrossed, can we write this as a recursion?

Explanation 1

  1. This is the exact same problem as the Longest Common Subsequence (LCS) problem.

  2. Dynamic init is dp[r][c] which represents the maximum number of connecting lines we can draw for A[:r] and B[:c] inclusive. We initialize dp have size dp[len(A)+1][len(B)+1].

  3. Dynamic base is if A or B is empty, in other words, top row and left column are initialized to 0.

  4. Dynamic function. If the last number of both A and B are the same, in other words, A[r-1] == B[c-1], then dp[r][c] = 1 + dp[r-1][c-1]. Else, we take the maximum of dp[r-1][c] and dp[r][c-1].

  5. Dynamic result is the bottom right number dp[len(A)][len(B)].

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func maxUncrossedLines(A []int, B []int) int {
    row, col := len(A), len(B)
    dp := make([][]int, row+1)
    for i := range dp {
        dp[i] = make([]int, col+1)
    }

    for r := 1; r < row+1; r++ {
        for c := 1; c < col+1; c++ {
            if A[r-1] == B[c-1] {
                dp[r][c] = 1 + dp[r-1][c-1]
            } else {
                dp[r][c] = max(dp[r-1][c], dp[r][c-1])
            }
        }
    }

    return dp[len(A)][len(B)]
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Explanation 2

  1. We can save space by using one dimensional array. Here we assume B’s length is less than A’s length.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func maxUncrossedLines(A []int, B []int) int {
    row, col := len(A), len(B)
    dp := make([]int, col+1)
    topLeft := 0

    for r := 1; r < row+1; r++ {
        for c := 1; c < col+1; c++ {
            temp := dp[c]
            if A[r-1] == B[c-1] {
                dp[c] = 1 + topLeft
            } else {
                dp[c] = max(dp[c], dp[c-1])
            }

            if c == col {
                topLeft = 0
            } else {
                topLeft = temp
            }
        }
    }

    return dp[len(B)]
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Contiguous Array

Given a binary array, find the maximum length of a contiguous subarray with equal number of 0 and 1.

Example 1:

1
2
3
Input: [0,1]
Output: 2
Explanation: [0, 1] is the longest contiguous subarray with equal number of 0 and 1.

Example 2:

1
2
3
Input: [0,1,0]
Output: 2
Explanation: [0, 1] (or [1, 0]) is a longest contiguous subarray with equal number of 0 and 1.

Note: The length of the given binary array will not exceed 50,000.

Explanation

  1. When we have any subarray problems, we can think of finding subarray’s accumulate sum to solve the problem. In this problem, if the current element is 0, we subtract 1; if the current element is 1, we plus 1. So if any subarray’s sum is 0, then this subarray will have equal number of 0 and 1.

  2. We will use a hash map to record the key is the sum, the value is the current index. If next time we have the same sum, then we know in between the subarray sum to 0, and this subarray’s length will be the current index i subtract hm.get(sum).

  3. Initially, we will put the entry {0, -1} into the hashmap. For example, if the input array is [0, 1]. When we iterate to number 0, we have sum equals to -1, and we put entry {-1, 0} into the hashmap. Then when we iterate to number 1, we have sum equals to 0. We check the hashmap has key 0, so we get the length by using current index subtract hm.get(0) and we get 1 - (-1) = 2.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func findMaxLength(nums []int) int {
    res := 0
    sum := 0
    hm := make(map[int]int)
    hm[0] = -1

    for i, num := range nums {
        if num == 0 {
            sum -= 1
        } else {
            sum += 1
        }
        if _, ok := hm[sum]; !ok {
            hm[sum] = i
        } else {
            res = max(res, i - hm[sum])
        }
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Possible Bipartition

Given a set of N people (numbered 1, 2, ..., N), we would like to split everyone into two groups of any size.

Each person may dislike some other people, and they should not go into the same group.

Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.

Return true if and only if it is possible to split everyone into two groups in this way.

Example 1:

1
2
3
Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]

Example 2:

1
2
Input: N = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false

Example 3:

1
2
Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false

Note:

  1. 1 <= N <= 2000

  2. 0 <= dislikes.length <= 10000

  3. 1 <= dislikes[i][j] <= N

  4. dislikes[i][0] < dislikes[i][1]

  5. There does not exist i != j for which dislikes[i] == dislikes[j].

Explanation

  1. This is a graph problem. Each pair of dislike, both numbers are connected by an edge. First, we can construct a graph using adjacent list to represent the input dislikes.

  2. Each vertex can belong to one of the two groups. We can create an array group and initialized every value be -1, which means all vertexes are not colored. group[i] represents the color that vertex i represents. If it belongs to group0, then group[i] = 0; if it belongs to group1, then group[i] = 1.

  3. We can use DFS to fill the color of every vertex. In the main function, loop through every vertex, if it doesn’t have color, then we pass the adjacent list, color array, current vertex, color 0 to the helper function and call it. If the DFS helper function returns false, then we immediately return false. After checking every vertex, we can return true.

  4. Inside the helper function, if the current vertex already has color, then we compare its color with the color we pass in, if they are the same, then we return true, else return false. Else the current vertex doesn’t have color, then we fill the current vertex with the color we pass in. Next, we loop through the current vertex’s neighbor vertex, and recursively call the helper function with a color that is different from the current vertex’s color. If in any iteration, the recursive function return false, then we return false immediately. Outside the loop, we return true.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
func possibleBipartition(N int, dislikes [][]int) bool {
    adjLst := make([][]int, N)
    for _, p := range dislikes {
        adjLst[p[0] - 1] = append(adjLst[p[0] - 1], p[1] - 1)
        adjLst[p[1] - 1] = append(adjLst[p[1] - 1], p[0] - 1)
    }

    group := make([]int, N)
    for i := range group {
        group[i] = -1
    }

    for v := 0; v < N; v++ {
        if group[v] == -1 && !dfs(adjLst, group, v, 0) {
            return false
        }
    }

    return true
}

func dfs(adjLst [][]int, group []int, v int, grp int) bool {
    if group[v] == -1 {
        group[v] = grp
    } else {
        return group[v] == grp
    }

    for _, adj := range adjLst[v] {
        if !dfs(adjLst, group, adj, 1-grp) {
            return false
        }
    }

    return true
}

Counting Bits

Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.

Example 1:

1
2
Input: 2
Output: [0,1,1]

Example 2:

1
2
Input: 5
Output: [0,1,1,2,1,2]

Follow up:

  • It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass?

  • Space complexity should be O(n).

  • Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.

Hint 1:

You should make use of what you have produced already.

Hint 2:

Divide the numbers in ranges like [2-3], [4-7], [8-15] and so on. And try to generate new range from previous.

Hint 3:

Or does the odd/even status of the number help you in calculating the number of 1s?

Explanation

  1. Iterate the input array starting from 1, if the current number is an even number, then res[i] = res[i/2]; if the current number is an odd number, then res[i] = res[i/2]+1.

  2. We can write out the result for number from 0 to 15.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
     0    0000    0
 -------------
 1    0001    1
 -------------
 2    0010    1
 3    0011    2
 -------------
 4    0100    1
 5    0101    2
 6    0110    2
 7    0111    3
 -------------
 8    1000    1
 9    1001    2
 10   1010    2
 11   1011    3
 12   1100    2
 13   1101    3
 14   1110    3
 15   1111    4

Solution

1
2
3
4
5
6
7
func countBits(num int) []int {
    res := make([]int, num+1)
    for i := 1; i <= num; i++ {
        res[i] = res[i/2] + i%2
    }
    return res
}

Week 5: May 29th–May 31st

Course Schedule

There are a total of numCourses courses you have to take, labeled from 0 to numCourses-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

Example 1:

1
2
3
4
Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
             To take course 1 you should have finished course 0. So it is possible.

Example 2:

1
2
3
4
5
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
             To take course 1 you should have finished course 0, and to take course 0 you should
             also have finished course 1. So it is impossible.

Constraints:

  • The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.

  • You may assume that there are no duplicate edges in the input prerequisites.

  • 1 <= numCourses <= 10^5

Hint 1:

This problem is equivalent to finding if a cycle exists in a directed graph. If a cycle exists, no topological ordering exists and therefore it will be impossible to take all courses.

Hint 2:

Topological Sort via DFS - A great video tutorial (21 minutes) on Coursera explaining the basic concepts of Topological Sort.

Hint 3:

Topological sort could also be done via BFS.

Explanation 1

  1. This is a graph problem. We will see the BFS method first. First, we need to make an adjancent list graph represented by a list of array. The index i sublist contains all the classes that are based on first taking prerequisites class i. Also, we make a one dimensional array prereq[] which count the number of classes that have to finish in order to take index class i .

  2. In BFS, we have a queue. First, loop through the prereq[] array, and enqueue all the classes that have 0 prerequisites to the queue. Now, while the queue is not empty, we dequeue one class p. And check the graph index p’s all the classes, subtract each of these classes’s number of prerequisites by 1 in the prereq array. If the number of prerequisites class is equal to 0, then we enqueue it to the queue.

  3. Now the queue is empty, that means we finish taking all the classes that have 0 prerequisites. We then loop through the prereq[] to see if every index class have value 0. If one of the index have more than 0 prerequisite class, we return false because we cannot take that index class since we already finish all the classes that have 0 prerequisites.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func canFinish(numCourses int, prerequisites [][]int) bool {
    adjLst := make([][]int, numCourses)
    prereq := make([]int, numCourses)
    queue := make([]int, 0)

    for _, p := range prerequisites {
        adjLst[p[1]] = append(adjLst[p[1]], p[0])
        prereq[p[0]] += 1
    }

    for i := 0; i < numCourses; i++ {
        if prereq[i] == 0 {
            queue = append(queue, i)
        }
    }

    for len(queue) != 0 {
        p := queue[0]
        queue = queue[1:]
        for _, c := range adjLst[p] {
            prereq[c] -= 1
            if prereq[c] == 0 { queue = append(queue, c) }
        }
    }

    for i := 0; i < numCourses; i++ {
        if prereq[i] != 0 { return false }
    }

    return true
}

Explanation 2

  1. We can also use DFS to solve this problem. First, we make a directed graph as above. Also, we need to make a one dimensional array visit[] which is used to record if the class i is visited or not. We use 0 as unvisit, 1 as visit, -1 as conflict. Since we use DFS, we can think of checking the classes linearly, if these classes make a circle, then it’s conflict and we return false.

  2. We loop through all the classes, for each class, we think of it as a starting point and use the helper function to check it.

  3. In the helper function, before we DFS into the deeper class, we mark the class in the visit array -1. So the base case is if the class is already mark as -1, then it means we make a circle, and we immediatly return false. After checking all the classes in index i, in other word, sublist of graph[i], we mark class i as visit 1. So the base case add one more condition, if visit[i] is 1, then we immediately return true since we confirm that base on starting point class i, all its advanced class do not make a circle.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func canFinish(numCourses int, prerequisites [][]int) bool {
    adjLst := make([][]int, numCourses)
    for _, p := range prerequisites {
        adjLst[p[0]] = append(adjLst[p[0]], p[1])
    }
    visited := make([]int, numCourses)

    for i := 0; i < numCourses; i++ {
        if !dfs(adjLst, visited, i) {
            return false
        }
    }

    return true
}

func dfs(adjLst [][]int, visited []int, course int) bool {
    if visited[course] == -1 { return false }
    if visited[course] == 1 { return true }

    visited[course] = -1
    for _, n := range adjLst[course] {
        if !dfs(adjLst, visited, n) { return false }
    }
    visited[course] = 1
    return true
}

K Closest Points to Origin

We have a list of points on the plane. Find the K closest points to the origin (0, 0).

(Here, the distance between two points on a plane is the Euclidean distance.)

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in.)

Example 1:

1
2
3
4
5
6
7
Input: points = [[1,3],[-2,2]], K = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest K = 1 points from the origin, so the answer is just [[-2,2]].

Example 2:

1
2
3
Input: points = [[3,3],[5,-1],[-2,4]], K = 2
Output: [[3,3],[-2,4]]
(The answer [[-2,4],[3,3]] would also be accepted.)

Note:

  1. 1 <= K <= points.length <= 10000

  2. -10000 < points[i][0] < 10000

  3. -10000 < points[i][1] < 10000

Explanation 1

  1. We can sort the input array points by distance, then return the first K points as a result, and this will take time $n log(n)$.

  2. We can also use a MaxHeap to store the fist K points first. Then iterate the rest of the points, for each iteration, we compare the current point with the MaxHeap’s top point’s distance. If the current point’s distance is smaller, then we pop the MaxHeap’s maximum point out, and insert the current point to the heap. This takes $n log(K)$ time. At the end, all the heap’s points are the first K closest points to the origin.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func kClosest(points [][]int, K int) [][]int {
    pq := &maxHeap{}
    heap.Init(pq)
    for _, point := range points {
        heap.Push(pq, point)
        if pq.Len() > K {
            heap.Pop(pq)
        }
    }

    res := make([][]int, 0)
    for pq.Len() > 0 {
        res = append(res, heap.Pop(pq).([]int))
    }

    return res
}

type maxHeap [][]int

func (h maxHeap) Len() int {
    return len(h)
}

func (h maxHeap) Less(i, j int) bool {
    distI := h[i][0] * h[i][0] + h[i][1] * h[i][1]
    distJ := h[j][0] * h[j][0] + h[j][1] * h[j][1]
    return distI > distJ
}

func (h maxHeap) Swap(i, j int) {
    h[i], h[j] = h[j], h[i]
}

func (h *maxHeap) Push(x interface{}) {
    *h = append(*h, x.([]int))
}

func (h *maxHeap) Pop() interface{} {
    old := *h
    item := old[len(old)-1]
    *h = old[:len(old)-1]
    return item
}

Explanation 2

  1. This problem asks us to find the first K short distance points and return them without sorting, so we can use quick select method to solve this problem in $O(N)$ average time complexity.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
func kClosest(points [][]int, K int) [][]int {
    left, right := 0, len(points) - 1
    for left <= right {
        p := partition(points, K, left, right)
        if p == K - 1 {
            return points[:K]
        } else if p < K - 1 {
            left = p + 1
        } else {
            right = p - 1
        }
    }

    return [][]int{}
}

func partition(points [][]int, K int, start, end int) int {
    firstPoint := points[start]
    firstPointDist := getDist(firstPoint)
    left, right := start + 1, end
    for left <= right {
        if getDist(points[left]) > firstPointDist && getDist(points[right]) < firstPointDist {
            points[left], points[right] = points[right], points[left]
        }
        if getDist(points[left]) <= firstPointDist { left += 1 }
        if getDist(points[right]) >= firstPointDist { right -= 1 }
    }
    points[start], points[right] = points[right], points[start]
    return right
}

func getDist(point []int) int {
    return point[0]*point[0] + point[1] * point[1]
}

Explanation 3

  1. We can sort the input array points by distance, then return the first K points as a result, and this will take time $n log(n)$. Here is using golang’s sort.Slice function.

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func kClosest(points [][]int, K int) [][]int {
    arr := make([]Node, 0)
    for _, point := range points {
        arr = append(arr, Node{Dist: point[0]*point[0]+point[1]*point[1], Point: point})
    }
    sort.Slice(arr, func (i, j int) bool {
        return arr[i].Dist < arr[j].Dist
    })

    res := make([][]int, 0)
    for i := 0; i < K; i++ {
        res = append(res, arr[i].Point)
    }

    return res
}

type Node struct {
    Dist int
    Point []int
}

Solution 4

  1. Here is using golang’s sort.Sort function.

Solution 4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func kClosest(points [][]int, K int) [][]int {
    sort.Sort(Points(points))
    return points[:K]
}

type Points [][]int

func (p Points) Len() int {
    return len(p)
}

func (p Points) Less(i, j int) bool {
    return p[i][0]*p[i][0]+p[i][1]*p[i][1] < p[j][0]*p[j][0]+p[j][1]*p[j][1]
}

func (p Points) Swap(i, j int) {
    p[i], p[j] = p[j], p[i]
}

Edit Distance

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

  1. Insert a character

  2. Delete a character

  3. Replace a character

Example 1:

1
2
3
4
5
6
Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation:
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

1
2
3
4
5
6
7
8
Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation:
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u')

Explanation 1

  1. We can use dynamic programming to solve this problem. For example, word1 = “12b45”, word2 = “abcde”. We can draw a dynamic table like below.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
         word2
          empty   a    b    c    d    e
 word1 +----------------------------------+
       |
 empty |    0     1    2    3    4    5
       |
    1  |    1     1    2    3
       |
    2  |    2     2    2    3
       |
    b  |    3     3    2    3
       |
    4  |    4     4    3    3
       |
    5  |    5
       +

  2. State is dp[r][c], which represents the minimum operation to convert word1[0, r-1] to word2[0, c-1].

  3. Init is when word1 is empty (top row), if word2 is also empty, then there are 0 operation to convert word1 to word2; if word2 has length 1, then there are 1 insert operation to convert word1 to word2; if word2 has length 2, then there are 2 insert operations to convert word1 to word2; if word3 has length 3, then we need 3 insert operations, etc.

  4. When word2 is empty (left most column), if word1 is also empty, then there are we need 0 operation; if word1 has length 1, then we need 1 remove operation; if word1 has length 2, then we need 2 remove operation, etc.

  5. Dynamic function is if the last character of both words are the same, for example, word1 = “12b”, word2 = “ab”, then the number of operations we need is the same as comparing word1 = “12” and word2 = “a”. In other words, if the last characters of both words are the same, then dp[r][c] = dp[r-1][c-1].

  6. If the last character of both words are not the same, for example, word1 = “12b4”, word2 = “abc”, then we need to consider three cases:

    1. Delete “4” from word1, then compare word1 = “12b” and word2 = “abc”. In other word, dp[r][c] = 1 + dp[r-1][c].

    2. Replace “4” with “c”, then compare word1 = “12b” and word2 = “ab”. In other word, dp[r][c] = 1 + dp[r-1][c-1].

    3. Insert “c” at the end of word1, then compare word1 = “12b4” and word2 = “ab”. In other word, dp[r][c] = 1 + dp[r][c-1].

  7. If the last character of both words are not the same, we should take the minimum among these 3 operations as the result of dp[r][c].

  8. Dynamic result is dp[len(word1)][len(word2)] which is at the bottom right.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func minDistance(word1 string, word2 string) int {
    dp := make([][]int, len(word1) + 1)
    for i := range dp {
        dp[i] = make([]int, len(word2) + 1)
    }

    for r := 0; r <= len(word1); r++ {
        for c := 0; c <= len(word2); c++ {
            if r == 0 {
                dp[r][c] = c
            } else if c == 0 {
                dp[r][c] = r
            } else if word1[r-1] == word2[c-1] {
                dp[r][c] = dp[r-1][c-1]
            } else {
                dp[r][c] = 1 + min(dp[r-1][c-1], min(dp[r-1][c], dp[r][c-1]))
            }
        }
    }

    return dp[len(word1)][len(word2)]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Explanation 2

  1. We can also save space by using a one dimensional array by comparing the topLeft, top, and left.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func minDistance(word1 string, word2 string) int {
    dp := make([]int, len(word2) + 1)
    topLeft := 0

    for r := 0; r <= len(word1); r++ {
        for c := 0; c <= len(word2); c++ {
            temp := dp[c]
            if r == 0 {
                dp[c] = c
            } else if c == 0 {
                dp[c] = r
            } else if word1[r-1] == word2[c-1] {
                dp[c] = topLeft
            } else {
                dp[c] = 1 + min(topLeft, min(dp[c], dp[c-1]))
            }
            if c == len(word2) {
                topLeft = 0
            } else {
                topLeft = temp
            }

        }
    }

    return dp[len(word2)]
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}