Sometimes is busy and want to skip a day, but I don’t want to break this continuous game. Let’s continue November LeetCoding Challenge.

Week 1: November 1st - November 7th

Meeting Rooms

Given an array of meeting time intervals where intervals[i] = [starti, endi], determine if a person could attend all meetings.

Example 1:

Input: intervals = [[0,30],[5,10],[15,20]]
Output: false

Example 2:

Input: intervals = [[7,10],[2,4]]
Output: true

Constraints:

0 <= intervals.length <= 10^4
intervals.length == 2
0 <= starti < endi <= 10^6

Explanation

For most interval problems, first we sort all intervals by their start time.
The only case two intervals not overlapping is the second interval’s start time is greater than or equal to the first interval’s end time.
We can loop over all intervals and checking if the current interval’s start time is less than the previous interval’s end time, then they are overlap, so we return false immediately. Outside the loop, that means no interval overlap, so we return true.

Solution

class Solution {
    public boolean canAttendMeetings(int[][] intervals) {
        if (intervals.length <= 1) return true;

        Arrays.sort(intervals, (a, b) -> {
            return a[0] - b[0];
        });

        int prevEnd = intervals[0][1];
        for (int i = 1; i < intervals.length; i++) {
            int curStart = intervals[i][0];
            if (curStart < prevEnd) return false;
            prevEnd = intervals[i][1];
        }

        return true;
    }
}

Convert Binary Number in a Linked List to Integer

Given head which is a reference node to a singly-linked list. The value of each node in the linked list is either 0 or 1. The linked list holds the binary representation of a number.

Return the decimal value of the number in the linked list.

Example 1:

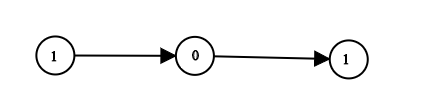
Input: head = [1,0,1]
Output: 5
Explanation: (101) in base 2 = (5) in base 10

Example 2:

Input: head = [0]
Output: 0

Example 3:

Input: head = [1]
Output: 1

Example 4:

Input: head = [1,0,0,1,0,0,1,1,1,0,0,0,0,0,0]
Output: 18880

Example 5:

Input: head = [0,0]
Output: 0

Constraints:

The Linked List is not empty.
Number of nodes will not exceed 30.
Each node’s value is either 0 or 1.

Hint 1:

Traverse the linked list and store all values in a string or array. convert the values obtained to decimal value.

Hint 2:

You can solve the problem in O(1) memory using bits operation. use shift left operation ( « ) and or operation ( | ) to get the decimal value in one operation.

Explanation

Initialize the result res equal to 0. Loop through all linked list elements. For each element, first we left shift res <<= 1, then add the current iterated element res += cur.val or using the OR operator to or the current iterated element res |= cur.val, then update the pointer to the next element.

Solution

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func getDecimalValue(head *ListNode) int {
    res := 0
    cur := head
    for cur != nil {
        res <<= 1
        res |= cur.Val
        cur = cur.Next
    }
    return res
}

Insertion Sort List

Sort a linked list using insertion sort.

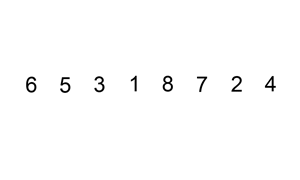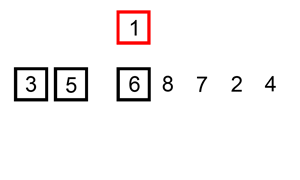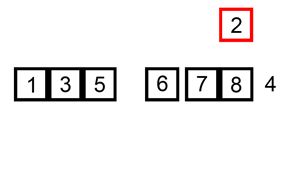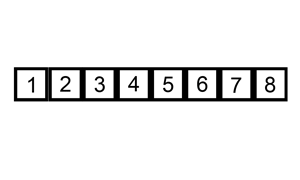
A graphical example of insertion sort. The partial sorted list (black) initially contains only the first element in the list. With each iteration one element (red) is removed from the input data and inserted in-place into the sorted list

Algorithm of Insertion Sort:

Insertion sort iterates, consuming one input element each repetition, and growing a sorted output list.
At each iteration, insertion sort removes one element from the input data, finds the location it belongs within the sorted list, and inserts it there.
It repeats until no input elements remain.

Example 1:

Input: 4->2->1->3
Output: 1->2->3->4

Example 2:

Input: -1->5->3->4->0
Output: -1->0->3->4->5

Explanation

First create a dummy node, and we need to have a cur pointer points at the dummy node, and lstPtr pointer points at the original list’s node for iterating.
While lstPtr is not null, we starts from lstPtr’s node, compare it with every cur.next’s node in the dummy list starts from the beginning of dummy list, here we also need a while loop to achieve this. If cur.next is null, or cur.next’s value is greater than lstPtr’s value, then we break out this inner while loop, and add lstPtr’s node to our dummy list.

Solution

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func insertionSortList(head *ListNode) *ListNode {
    dummy, lstPtr := &ListNode{Val: -1}, head

    for lstPtr != nil {
        temp := lstPtr.Next
        cur := dummy
        for cur.Next != nil && cur.Next.Val <= lstPtr.Val {
            cur = cur.Next
        }
        lstPtr.Next = cur.Next
        cur.Next = lstPtr
        lstPtr = temp
    }

    return dummy.Next
}

Consecutive Characters

Given a string s, the power of the string is the maximum length of a non-empty substring that contains only one unique character.

Return the power of the string.

Example 1:

Input: s = "leetcode"
Output: 2
Explanation: The substring "ee" is of length 2 with the character 'e' only.

Example 2:

Input: s = "abbcccddddeeeeedcba"
Output: 5
Explanation: The substring "eeeee" is of length 5 with the character 'e' only.

Example 3:

Input: s = "triplepillooooow"
Output: 5

Example 4:

Input: s = "hooraaaaaaaaaaay"
Output: 11

Example 5:

Input: s = "tourist"
Output: 1

Constraints:

1 <= s.length <= 500
s contains only lowercase English letters.

Hint 1:

Keep an array power where power[i] is the maximum power of the i-th character.

Hint 2:

The answer is max(power[i]).

Explanation

We can use brute force one iteration to solve this problem.
Initially we define the current character curChar = s[0], current count cnt = 1, and the result is res = 1. Start looping from the second character to the last character. For each character s[i], we compare it with curChar. If they are equal, then we just increase the count cnt. Else, we update the res = max(res, cnt), and reset curChar = s[i] and reset the count cnt = 1.
One edge case is all characters are the same. For example, s = "cc", after the loop, we need to update the res = max(res, cnt).

Solution

func maxPower(s string) int {
    res := 1
    curChar, cnt := s[0], 1

    for i := 1; i < len(s); i++ {
        if s[i] == curChar {
            cnt += 1
        } else {
            res = max(res, cnt)
            curChar = s[i]
            cnt = 1
        }
    }
    res = max(res, cnt)

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Minimum Height Trees

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [ai, bi] indicates that there is an undirected edge between the two nodes ai and bi in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs’ root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

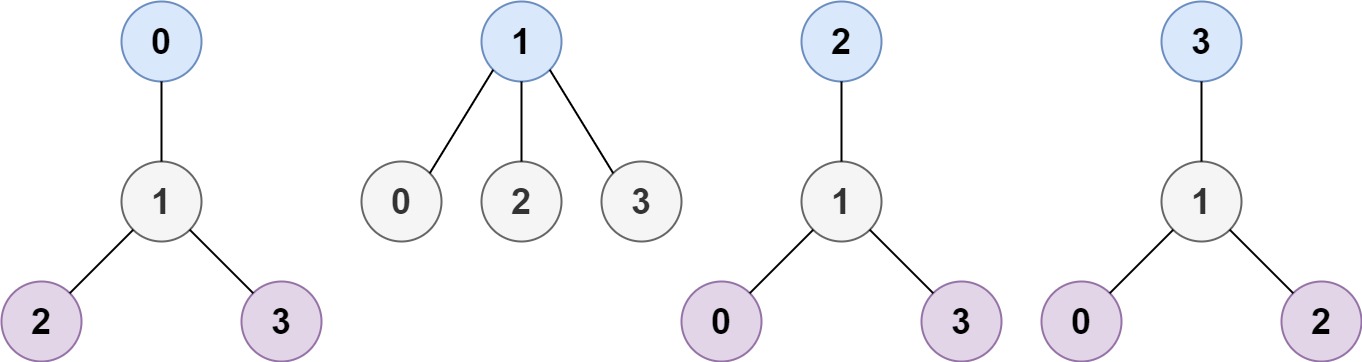
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

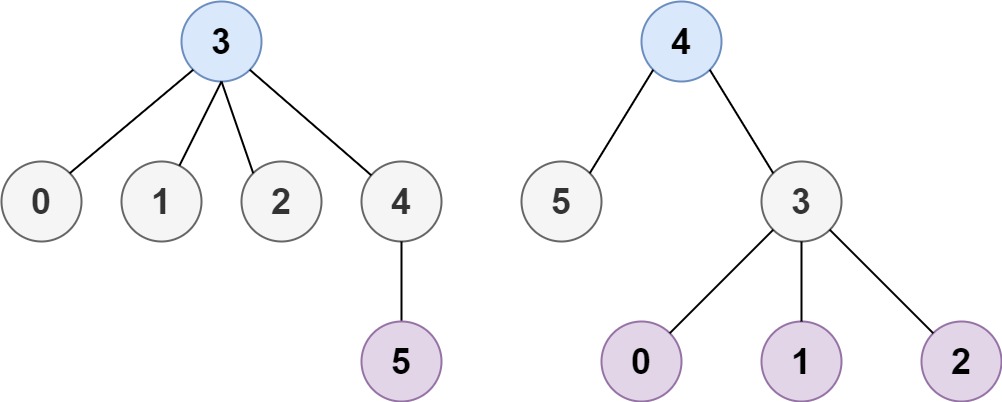
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Example 3:

Input: n = 1, edges = []
Output: [0]

Example 4:

Input: n = 2, edges = [[0,1]]
Output: [0,1]

Constraints:

1 <= n <= 2 * 10^4
edges.length == n - 1
0 <= ai, bi < n
ai != bi
All the pairs (ai, bi) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

Hint 1:

How many MHTs can a graph have at most?

Explanation

We can use topological sort to solve this problem. First, we need to create an adjancent list based on the edges[][]. Then, loop through the adjacent list and update node i’s in degree in inDegree[]. Then, we add all leaves node (which has only one adjancent node or in degree is 1) to the queue.
We know that if there is one node, then we can return that node as the result. If there are two nodes, then we can return both nodes as the result. If there are three nodes, we will remove two leaves node, and now we only has one node, and that one node is the result.
The queue will contain all leaves nodes. After we add all leaves nodes to the queue, while n > 2, we want to delete all leaves node, so we updated n to be subtracted the size of the queue. Then poll all the leaves nodes from the queue, iterate these leaves nodes’ neighbors, subtract these neighbor’s indegree by 1. Repeat the above process. When n <= 2, the remain one or two nodes in the queue will be the final result.

Solution

func findMinHeightTrees(n int, edges [][]int) []int {
    if n == 1 { return []int{0} }
    if n == 2 { return []int{0, 1} }

    adjLst := make([][]int, n)
    for i := range adjLst {
        adjLst[i] = make([]int, 0)
    }
    for i := range edges {
        a := edges[i][0]
        b := edges[i][1]
        adjLst[a] = append(adjLst[a], b)
        adjLst[b] = append(adjLst[b], a)
    }

    inDegree := make([]int, n)
    for i := range adjLst {
        for _, neighbor := range adjLst[i] {
            inDegree[neighbor] += 1
        }
    }

    leaves := make([]int, 0)

    for i := range inDegree {
        if inDegree[i] == 1 {
            leaves = append(leaves, i)
        }
    }

    for n > 2 {
        n -= len(leaves)
        for i := len(leaves) - 1; i >= 0; i-- {
            leaf := leaves[0]
            leaves = leaves[1:]
            for _, neighbor := range adjLst[leaf] {
                inDegree[neighbor] -= 1
                if inDegree[neighbor] == 1 {
                    leaves = append(leaves, neighbor)
                }
            }
        }
    }

    return leaves
}

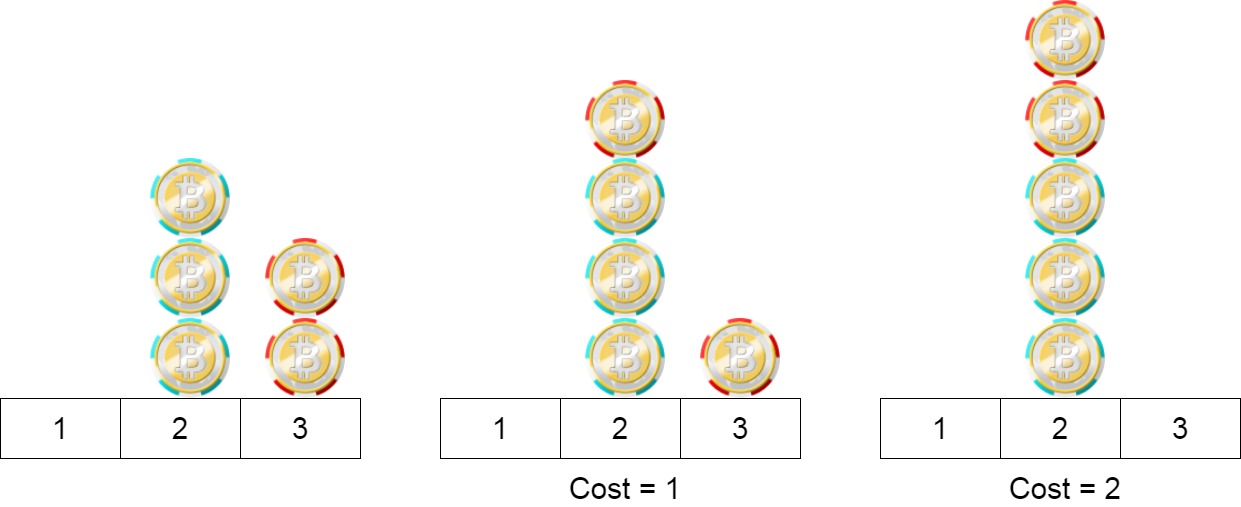
Minimum Cost to Move Chips to The Same Position

We have n chips, where the position of the ith chip is position[i].

We need to move all the chips to the same position. In one step, we can change the position of the ith chip from position[i] to:

position[i] + 2 or position[i] - 2 with cost = 0.
position[i] + 1 or position[i] - 1 with cost = 1.

Return the minimum cost needed to move all the chips to the same position.

Example 1:

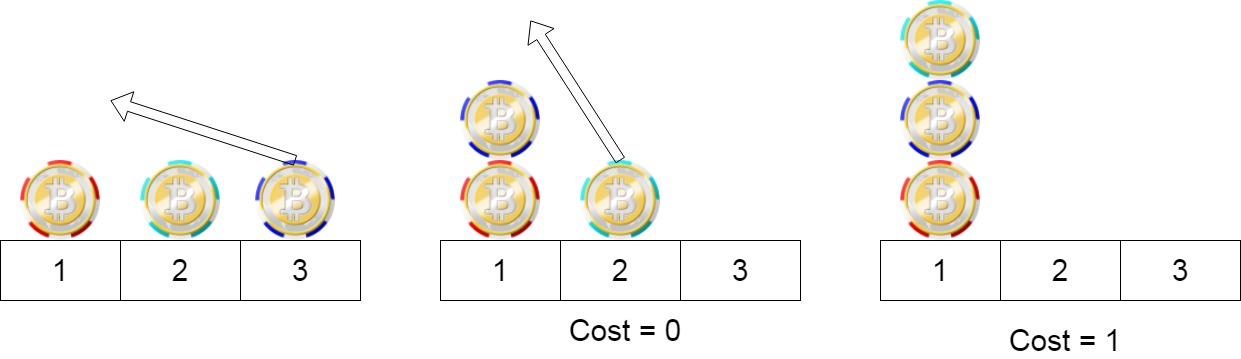
Input: position = [1,2,3]
Output: 1
Explanation: First step: Move the chip at position 3 to position 1 with cost = 0.
Second step: Move the chip at position 2 to position 1 with cost = 1.
Total cost is 1.

Input: position = [2,2,2,3,3]
Output: 2
Explanation: We can move the two chips at poistion 3 to position 2. Each move has cost = 1. The total cost = 2.

Example 3:

Input: position = [1,1000000000]
Output: 1

Constraints:

1 <= position.length <= 100
1 <= position[i] <= 10^9

Hint 1:

The first move keeps the parity of the element as it is.

Hint 2:

The second move changes the parity of the element.

Hint 3:

Since the first move is free, if all the numbers have the same parity, the answer would be zero.

Hint 4:

Find the minimum cost to make all the numbers have the same parity.

Explanation

We can think that first moving all even chips to position 0 and all odd chips to position 1, so this cost is 0. Then we have two piles on position 0 and position 1. Now, the result is the minimum between these two piles.

Solution

func minCostToMoveChips(position []int) int {
    odd, even := 0, 0

    for _, p := range position {
        if p % 2 == 0 {
            even += 1
        } else {
            odd += 1
        }
    }

    if odd < even {
        return odd
    } else {
        return even
    }
}

Find the Smallest Divisor Given a Threshold

Given an array of integers nums and an integer threshold, we will choose a positive integer divisor and divide all the array by it and sum the result of the division. Find the smallest divisor such that the result mentioned above is less than or equal to threshold.

Each result of division is rounded to the nearest integer greater than or equal to that element. (For example: 7/3 = 3 and 10/2 = 5).

It is guaranteed that there will be an answer.

Example 1:

Input: nums = [1,2,5,9], threshold = 6
Output: 5
Explanation: We can get a sum to 17 (1+2+5+9) if the divisor is 1.
If the divisor is 4 we can get a sum to 7 (1+1+2+3) and if the divisor is 5 the sum will be 5 (1+1+1+2).

Example 2:

Input: nums = [2,3,5,7,11], threshold = 11
Output: 3

Example 3:

Input: nums = [19], threshold = 5
Output: 4

Constraints:

1 <= nums.length <= 5 * 10^4
1 <= nums[i] <= 10^6
nums.length <= threshold <= 10^6

Hint 1:

Examine every possible number for solution. Choose the largest of them.

Hint 2:

Use binary search to reduce the time complexity.

Explanation

Brute force approach would be to try all the possible divisors from 1 to max(nums).
We can optimize it using binary search method to find the smallest divisor such that the result mentioned above is less than or equal to threshold.

Solution

func smallestDivisor(nums []int, threshold int) int {
    left, right := 1, 1
    for _, num := range nums {
        if (num > right) {
            right = num
        }
    }

    for left < right {
        mid := left + (right - left) / 2
        sum := 0
        for _, num := range nums {
            sum += (num - 1) / mid + 1
        }
        if sum <= threshold {
            right = mid
        } else {
            left = mid + 1
        }
    }

    return left
}

Add Two Numbers II

You are given two non-empty linked lists representing two non-negative integers. The most significant digit comes first and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.

You may assume the two numbers do not contain any leading zero, except the number 0 itself.

Follow up:

What if you cannot modify the input lists? In other words, reversing the lists is not allowed.

Example:

Input: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 8 -> 0 -> 7

Explanation

We can use two stacks to store two iterated node’s value respectivly. Also, we create a ListNode res to have value 0 initialy. Since stack is Last In First Out, while either of the stack is not empty, we can use a variable sum to sum the pop value. And update res.value = sum / 10. Then, we create a new ListNode head to default have value sum / 10, then make head.next = res, then update the res pointer to point to the head, and update sum = sum / 10. When outside of the loop, if res has value 0, then we return head.next, else just return res.

Solution

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
    s1, s2 := make([]int, 0), make([]int, 0)
    cur1, cur2 := l1, l2
    for cur1 != nil {
        s1 = append(s1, cur1.Val)
        cur1 = cur1.Next
    }
    for cur2 != nil {
        s2 = append(s2, cur2.Val)
        cur2 = cur2.Next
    }

    res := new(ListNode)
    sum := 0
    for len(s1) > 0 || len(s2) > 0 {
        if len(s1) > 0 {
            sum += s1[len(s1)-1]
            s1 = s1[:len(s1)-1]
        }
        if len(s2) > 0 {
            sum += s2[len(s2)-1]
            s2 = s2[:len(s2)-1]
        }
        res.Val = sum % 10
        head := &ListNode{Val: sum / 10}
        head.Next = res
        res = head
        sum = sum / 10
    }

    if res.Val == 0 {
        return res.Next
    } else {
        return res
    }
}

Week 2: November 8th - November 14th

Two Sum Less Than K

Given an array A of integers and integer K, return the maximum S such that there exists i < j with A[i] + A[j] = S and S < K. If no i, j exist satisfying this equation, return -1.

Example 1:

Input: A = [34,23,1,24,75,33,54,8], K = 60
Output: 58
Explanation: We can use 34 and 24 to sum 58 which is less than 60.

Example 2:

Input: A = [10,20,30], K = 15
Output: -1
Explanation: In this case it is not possible to get a pair sum less that 15.

Constraints:

1 <= A.length <= 100
1 <= A[i] <= 1000
1 <= K <= 2000

Hint 1:

What if we have the array sorted?

Hint 2:

Loop the array and get the value A[i] then we need to find a value A[j] such that A[i] + A[j] < K which means A[j] < K - A[i]. In order to do that we can find that value with a binary search.

Explanation

Similar to 167. Two Sum II - Input array is sorted, we can use two pointers approach to solve this problem.
First, sort the array. Then create a pointer left points to index 0, another pointer right points to the last index.
While left < right, we calculate the sum = A[left] + A[right]. If sum is less than K, then we update the res and increase left pointer. Else we decrease right pointer.

Solution

class Solution {
    public int twoSumLessThanK(int[] A, int K) {
        int res = -1;
        Arrays.sort(A);
        int left = 0, right = A.length - 1;

        while (left < right) {
            int sum = A[left] + A[right];
            if (sum < K) {
                res = Math.max(res, sum);
                left += 1;
            } else {
                right -= 1;
            }
        }

        return res;
    }
}

Binary Tree Tilt

Given the root of a binary tree, return the sum of every tree node’s tilt.

The tilt of a tree node is the absolute difference between the sum of all left subtree node values and all right subtree node values. If a node does not have a left child, then the sum of the left subtree node values is treated as 0. The rule is similar if there the node does not have a right child.

Example 1:

Input: root = [1,2,3]
Output: 1
Explanation:
Tilt of node 2 : |0-0| = 0 (no children)
Tilt of node 3 : |0-0| = 0 (no children)
Tile of node 1 : |2-3| = 1 (left subtree is just left child, so sum is 2; right subtree is just right child, so sum is 3)
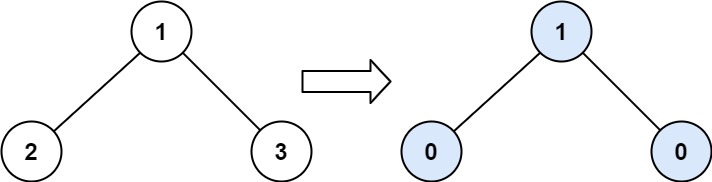
Sum of every tilt : 0 + 0 + 1 = 1

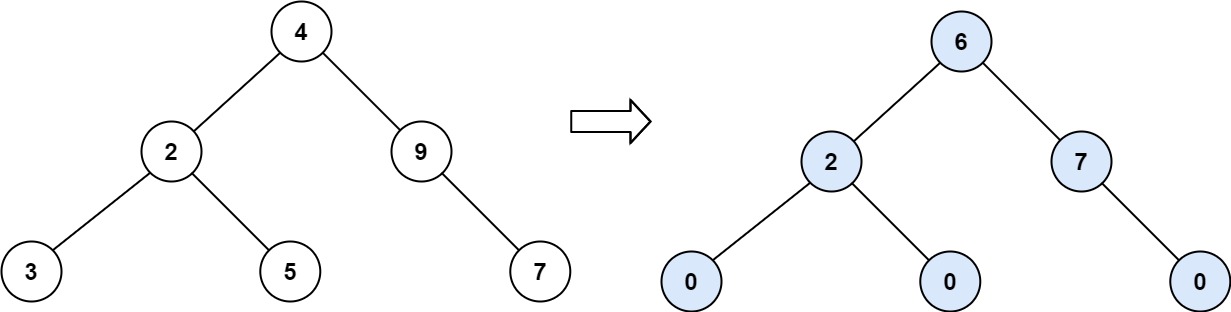
Example 2:

Input: root = [4,2,9,3,5,null,7]
Output: 15
Explanation:
Tilt of node 3 : |0-0| = 0 (no children)
Tilt of node 5 : |0-0| = 0 (no children)
Tilt of node 7 : |0-0| = 0 (no children)
Tilt of node 2 : |3-5| = 2 (left subtree is just left child, so sum is 3; right subtree is just right child, so sum is 5)
Tilt of node 9 : |0-7| = 7 (no left child, so sum is 0; right subtree is just right child, so sum is 7)
Tilt of node 4 : |(3+5+2)-(9+7)| = |10-16| = 6 (left subtree values are 3, 5, and 2, which sums to 10; right subtree values are 9 and 7, which sums to 16)
Sum of every tilt : 0 + 0 + 0 + 2 + 7 + 6 = 15

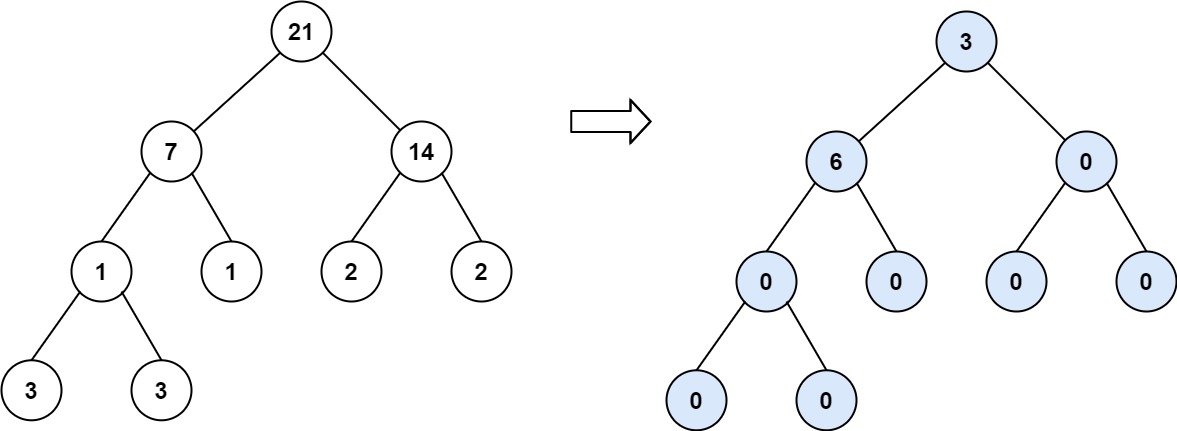
Example 3:

Input: root = [21,7,14,1,1,2,2,3,3]
Output: 9

Constraints:

The number of nodes in the tree is in the range [0, 10^4].
-1000 <= Node.val <= 1000

Hint 1:

Don’t think too much, this is an easy problem. Take some small tree as an example.

Hint 2:

Can a parent node use the values of its child nodes? How will you implement it?

Hint 3:

May be recursion and tree traversal can help you in implementing.

Hint 4:

What about postorder traversal, using values of left and right childs?

Explanation

We can also use post-order traversal to solve this problem. In order to find the root node’s tilt, we need to know the left subtree’s sum and the right subtree’s sum. In the method of getSum, if we use post-order traversal to find the sum of the tree, we also calculate the left subtree’s sum and right subtree’s sum first then plus the root value. So, in the getSum method, after we find out the left subtree and right subtree’s sum and before return the sum, we can calculate the tilt for the root since the root node’s tilt is depends on the left subtree’s sum and right subtree’s sum.
Using post-order traversal, every node will be a root, in other words, we are iterating every node. We will create a reference pointing to variable res to accumulate every node’s tilt.

Solution

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func findTilt(root *TreeNode) int {
    res := 0
    getSum(root, &res)
    return res
}

func getSum(root *TreeNode, res *int) int {
    if root == nil { return 0 }

    leftSum := getSum(root.Left, res)
    rightSum := getSum(root.Right, res)

    if leftSum < rightSum {
        *res += rightSum - leftSum
    } else {
        *res += leftSum - rightSum
    }

    return root.Val + leftSum + rightSum
}

Maximum Difference Between Node and Ancestor

Given the root of a binary tree, find the maximum value V for which there exist different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.

Example 1:

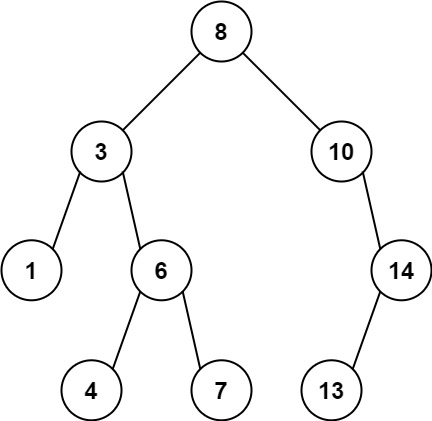
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Example 2:

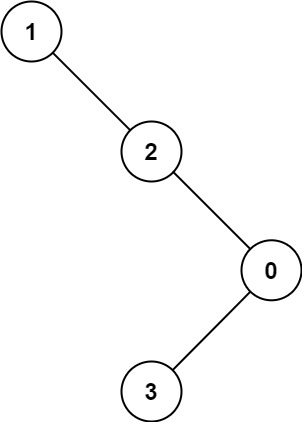
Input: root = [1,null,2,null,0,3]
Output: 3

Constraints:

The number of nodes in the tree is in the range [2, 5000].
0 <= Node.val <= 10^5

Hint 1:

For each subtree, find the minimum value and maximum value of its descendants.

Explanation

For each node, we need the minimum and maximum values from the ancestor. So we can use pre-order traversal to pass down the minimum value and maximum value to the current node’s left child and right child.
Create a helper function which accept the current node, minimum and maximum values and they both initially set to current node’s value. Inside the helper function, we can use the current node’s value to compare with minimum value and maximum value to get the maximum absolute difference and update the result. Then we update the minimum value and maximum value that compares with the current node’s value. Next, recursively pass down the updated minimum and maximum values to left child and right child. At the end, return the maximum result.

Solution

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxAncestorDiff(root *TreeNode) int {
    res := 0
    helper(root, root.Val, root.Val, &res)
    return res
}

func helper(root *TreeNode, parentMin, parentMax int, res *int) {
    if (root == nil) { return }

    a := abs(root.Val - parentMin)
    b := abs(root.Val - parentMax)
    *res = max(*res, max(a, b))

    curMin := min(root.Val, parentMin)
    curMax := max(root.Val, parentMax)
    helper(root.Left, curMin, curMax, res)
    helper(root.Right, curMin, curMax, res)
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

func abs(num int) int {
    if num < 0 {
        return -num
    } else {
        return num
    }
}

Flipping an Image

Given a binary matrix A, we want to flip the image horizontally, then invert it, and return the resulting image.

To flip an image horizontally means that each row of the image is reversed. For example, flipping [1, 1, 0] horizontally results in [0, 1, 1].

To invert an image means that each 0 is replaced by 1, and each 1 is replaced by 0. For example, inverting [0, 1, 1] results in [1, 0, 0].

Example 1:

Input: [[1,1,0],[1,0,1],[0,0,0]]
Output: [[1,0,0],[0,1,0],[1,1,1]]
Explanation: First reverse each row: [[0,1,1],[1,0,1],[0,0,0]].
Then, invert the image: [[1,0,0],[0,1,0],[1,1,1]]

Example 2:

Input: [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
Output: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
Explanation: First reverse each row: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]].
Then invert the image: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]

Notes:

1 <= A.length = A[0].length <= 20
0 <= A[i][j] <= 1

Explanation

We can use brute force to solve this problem.
If the current row is [0, 1, 0]. Let left points to the beginning of index 0 and right points to the end of index 2. After flipping, A[left] = A[right] = 0 stays the same. Then after inverting, we get A[left] = A[right] = 1. Therefore, if A[left] = A[right], after flipping and inverting, A[left] and A[right] change from 0 to 1, or 1 to 0.
If the current row is [1, 0]. Let left points to the beginning of index 0 and right points to the end of index 1. After flipping, we get [0, 1], then after inverting, we get [1, 0] which is the same as the original array. Therefore, if A[left] and A[right] are different, then after flipping and inverting, they stay the same.

Solution

func flipAndInvertImage(A [][]int) [][]int {
    row, col := len(A), len(A[0])

    for r := 0; r < row; r++ {
        for left, right := 0, col - 1; left <= right; left, right = left + 1, right - 1 {
            if A[r][left] == A[r][right] {
                A[r][left] = 1 - A[r][left]
                A[r][right] = A[r][left]
            }
        }
    }

    return A
}

Valid Square

Given the coordinates of four points in 2D space, return whether the four points could construct a square.

The coordinate (x,y) of a point is represented by an integer array with two integers.

Example:

Input: p1 = [0,0], p2 = [1,1], p3 = [1,0], p4 = [0,1]
Output: True

Note:

All the input integers are in the range [-10000, 10000].
A valid square has four equal sides with positive length and four equal angles (90-degree angles).
Input points have no order.

Explanation

We cannot just find if two points have the same x-axis or y-axis, we also need to think about all 4 lengths will be equal. So, we can iterate every two points and find their distance and store the distance into the set. If the set have element 0, that means there are two points on the same position so we return false. Or if the set does not cantains 2 elemnts, we also return false because in a square 1 distance is the square length, another distance will be the diagonal length.

Solution

func validSquare(p1 []int, p2 []int, p3 []int, p4 []int) bool {
    set := make(map[int]bool)
    set[getDistance(p1, p2)] = true
    set[getDistance(p1, p3)] = true
    set[getDistance(p1, p4)] = true
    set[getDistance(p2, p3)] = true
    set[getDistance(p2, p4)] = true
    set[getDistance(p3, p4)] = true
    return set[0] == false && len(set) == 2
}

func getDistance(a []int, b []int) int {
    return (b[0] - a[0]) * (b[0] - a[0]) + (b[1] - a[1]) * (b[1] - a[1]);
}

Permutations II

Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.

Example 1:

Input: nums = [1,1,2]
Output:
[[1,1,2],
 [1,2,1],
 [2,1,1]]

Example 2:

Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Constraints:

1 <= nums.length <= 8
-10 <= nums[i] <= 10

Explanation

Similar to 46. Permutations, but this time there are duplicated numbers in the input list, and we don’t want the result list have duplicated sublist.
First, we can sort the input list. We still need a temp list for storing the sublist, and a visited array to check whether the element have been visited or not. Inside the helper method, the base case is if the temp list has length equals to the input array, then we add the temp list as sublist into the result list, and return.
To remove duplicated elements, under the for loop, we can check if i > 0 && nums[i] == nums[i-1] && visited[i-1] == false, then we ignore the current nums[i]. From the above example, we want the first 1, second 1, and 2; in this case, when we iterate to the second 1, it satisify i > 0 && nums[i] == nums[i-1], and now visited[i-1] = visited[0] = true. We don’t want the second 1, first 1, and 2; in this case, when we iterate to the second 1, it satisify i > 0 && nums[i] == nums[i-1] and visited[i-1] = visited[0] = false.

Solution

func permuteUnique(nums []int) [][]int {
    res := make([][]int, 0)
    temp := make([]int, 0)
    visited := make(map[int]bool)
    sort.Ints(nums)
    helper(nums, temp, &res, visited)
    return res
}

func helper(nums []int, temp []int, res *[][]int, visited map[int]bool) {
    if len(temp) == len(nums) {
        builder := make([]int, len(temp))
        copy(builder, temp)
        *res = append(*res, builder)
        return
    }

    for i := range nums {
        if visited[i] == true { continue }
        if i > 0 && nums[i] == nums[i-1] && visited[i-1] == false { continue }
        temp = append(temp, nums[i])
        visited[i] = true
        helper(nums, temp, res, visited)
        temp = temp[:len(temp)-1]
        visited[i] = false
    }
}

Populating Next Right Pointers in Each Node

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

You may only use constant extra space.
Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

The number of nodes in the given tree is less than 4096.
-1000 <= node.val <= 1000

Explanation 1

We can use recursion method here. Since this is a perfect binary tree, if the root node has left node, then it must has right node, so we can check if it has left node first, then connect it with its right node. To connect the right node’s next node, we first check its parent node has next node, if it has, then we can connect the right node’s next to its parent node’s left node.

Solution 1

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil { return root }
    if root.Left != nil {
        root.Left.Next = root.Right
    }
    if root.Right != nil && root.Next != nil {
        root.Right.Next = root.Next.Left
    }
    connect(root.Left)
    connect(root.Right)
    return root
}

Explanation 2

We can use a O(1) space iterative method to solve this problem. We create a start pointer that points to the current level’s beginning, a cur pointer that is used to iterate the current level’s node.

Solution 2

/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Next *Node
 * }
 */

func connect(root *Node) *Node {
    if root == nil { return root }
    start := root
    cur := start

    for start != nil {
        cur = start
        for cur != nil {
            if cur.Left != nil {
                cur.Left.Next = cur.Right
            }
            if cur.Right != nil && cur.Next != nil {
                cur.Right.Next = cur.Next.Left
            }
            cur = cur.Next
        }
        start = start.Left
    }

    return root
}

Poor Pigs

There are 1000 buckets, one and only one of them is poisonous, while the rest are filled with water. They all look identical. If a pig drinks the poison it will die within 15 minutes. What is the minimum amount of pigs you need to figure out which bucket is poisonous within one hour?

Answer this question, and write an algorithm for the general case.

General case:

If there are n buckets and a pig drinking poison will die within m minutes, how many pigs (x) you need to figure out the poisonous bucket within p minutes? There is exactly one bucket with poison.

Note:

A pig can be allowed to drink simultaneously on as many buckets as one would like, and the feeding takes no time.
After a pig has instantly finished drinking buckets, there has to be a cool down time of m minutes. During this time, only observation is allowed and no feedings at all.
Any given bucket can be sampled an infinite number of times (by an unlimited number of pigs).

Hint 1:

What if you only have one shot? Eg. 4 buckets, 15 mins to die, and 15 mins to test.

Hint 2:

How many states can we generate with x pigs and T tests?

Hint 3:

Find minimum x such that (T+1)^x >= N

Explanation

For example, if we only have 1 pig, and 15 minutes, how many buckets can we test? The answer is 2 because we let the pig drinks any 1 of the 2 bucket, if it die, then that bucket is poisonous. If it doesn’t die, then another bucket is poisonous.
Now if we have 2 pigs and 15 minutes, how many buckets can we test? The answer is 4 because pig1 drinks bucketA, pig2 drinks bucketB, then both pigs drink bucketC. If one pig1 is dead, that means bucketA is poisonous. If pig2 is dead, that means bucketB is poisonous. If both pigs dead, that means bucktC is poisonous. If both pig not dead, that means bucketD is poisonous. Similarlly, 3 pigs and 15 minutes can test 8 buckets, which is 2^3=8.
If we only have 15 minutes, that means we can only test one time, it’s a one dimensional array. If we have 2 pigs and 30 minutes, that means we can test two times, it’s a two dimensional array. The buckets we can test is 9. For example:
1
2
3
4
5
1 2 3 4 5 6 7 8 9
First, we let pig1 drink bucket 1, 2, 3, and pig2 drink bucket 1, 4, 7. After 15 minutes, we let pig1 drink bucket 4, 5, 6, and pig2 drink bucket 2, 5, 8. At the end, if both pig not dead, that means bucket9 is poisonous. If within the first 15minutes, pig1 dead after drinking bucket 1, 2, 3, and pig2 also dead within the first 15minutes. That means bucket1 is poisonous. If within the first 15minutes, pig1 dead, but pig2 not dead, then pig2 drink bucket 2, 5, 8. Now if pig2 also dead, that means bucket2 is poinsonous. The total bucket is 3^2=9.
If we have 3 pigs, that means it’s a 3 dimensional array, also within 30 minutes, test 2 times, then the buckets we can test becomes 3^3=27.
This problem ask us to calculate the minimun number of pigs to test n buckets, so we need to make the dimensional as small as possible, in other words, the row and column be as big as possible. The number of row and column can be calculated as the number of times we can test plus 1. We can calculate the number of times we can test by minutesToTest / minutesToDie. So, the number of row and column m is equal to minutesToTest / minutesToDie + 1. If we have x pigs, then the total bucket is equals to t=m^x. We can calculate x = log(t)/log(m).

Solution

func poorPigs(buckets int, minutesToDie int, minutesToTest int) int {
    m := float64(minutesToTest / minutesToDie + 1)
    return int(math.Ceil(math.Log(float64(buckets)) / math.Log(m)))
}

Week 3: November 15th - November 21st

Remove Interval

Given a sorted list of disjoint intervals, each interval intervals[i] = [a, b] represents the set of real numbers x such that a <= x < b.

We remove the intersections between any interval in intervals and the interval toBeRemoved.

Return a sorted list of intervals after all such removals.

Example 1:

Input: intervals = [[0,2],[3,4],[5,7]], toBeRemoved = [1,6]
Output: [[0,1],[6,7]]

Example 2:

Input: intervals = [[0,5]], toBeRemoved = [2,3]
Output: [[0,2],[3,5]]

Example 3:

Input: intervals = [[-5,-4],[-3,-2],[1,2],[3,5],[8,9]], toBeRemoved = [-1,4]
Output: [[-5,-4],[-3,-2],[4,5],[8,9]]

Constraints:

1 <= intervals.length <= 10^4
-10^9 <= intervals[i][0] < intervals[i][1] <= 10^9

Hint 1:

Solve the problem for every interval alone.

Hint 2:

Divide the problem into cases according to the position of the two intervals.

Explanation

We can consider different cases and solve this problem in one loop.

Case 1 if removeStart <= curStart && curEnd <= removeEnd, then we don’t add any interval.

                 curStart----------curEnd
 removeStart-------------------------------------removeEnd

Case 2 else if curStart <= removeStart && removeEnd <= curEnd, then we add two intervals [curStart, removeStart] and [removeEnd, curEnd].
1
2
curStart-------------------------------------curEnd removeStart----------removeEnd

Case 3 else if curEnd <= removeStart, then we add an interval [curStart, curEnd]

 curStart---------------curEnd
                                     removeStart-------removeEnd

Case 4 else if curStart >= removeEnd, then we add an interval [curStart, curEnd]

                                     curStart---------------curEnd
 removeStart-------removeEnd

Case 5 else if curStart <= removeStart && curEnd <= removeEnd, then we add an interval [curStart, removeStart].
1
2
curStart-------------------------curEnd removeStart--------------------------removeEnd

Case 6 else if curStart <= removeend && curEnd >= removeEnd, then we add an interval [removeEnd, curEnd].

                 curStart---------------------------curEnd
 removeStart------------------------removeEnd

Solution

class Solution {
    public List<List<Integer>> removeInterval(int[][] intervals, int[] toBeRemoved) {
        List<List<Integer>> res = new ArrayList<>();
        int removeStart = toBeRemoved[0];
        int removeEnd = toBeRemoved[1];

        for (int i = 0; i < intervals.length; i++) {
            int curStart = intervals[i][0];
            int curEnd = intervals[i][1];
            if (removeStart <= curStart && curEnd <= removeEnd) continue;

            if (curStart <= removeStart && removeEnd <= curEnd) {
                if (curStart != removeStart) res.add(Arrays.asList(curStart, removeStart));
                if (removeEnd != curEnd) res.add(Arrays.asList(removeEnd, curEnd));
            } else if (curEnd <= removeStart) {
                res.add(Arrays.asList(curStart, curEnd));
            } else if (curStart >= removeEnd) {
                res.add(Arrays.asList(curStart, curEnd));
            } else if (curEnd <= removeEnd) {
                res.add(Arrays.asList(curStart, removeStart));
            } else {
                res.add(Arrays.asList(removeEnd, curEnd));
            }
        }

        return res;
    }
}

Range Sum of BST

Given the root node of a binary search tree, return the sum of values of all nodes with a value in the range [low, high].

Example 1:

Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32

Example 2:

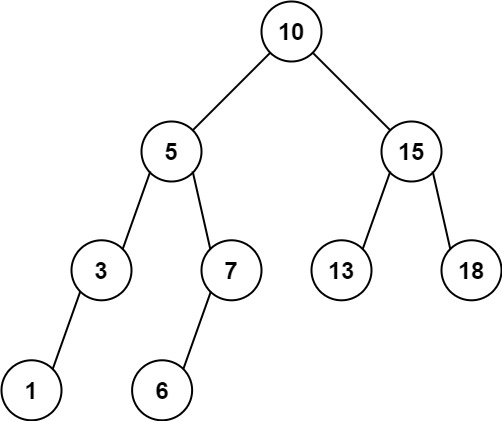
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23

Constraints:

The number of nodes in the tree is in the range [1, 2 * 104].
1 <= Node.val <= 10^5
1 <= low <= high <= 10^5
All Node.val are unique.

Explanation

First we think of some base cases. If root node is NULL, we return 0. If root node value is not in the range, then it’s either less than low or greater than high.
If root node value is less than low, then we can ignore the root node and its left subtree, so we recursively call the main function with root.Right as the new root. Else if root node value is greater than high, then we can ignore the root node and its right subtree, so we recursively call the main function with root.Left as the new root. Else that means root node value is in the range, so we return the sum of root.Val and the results for both recursive functions with the left child node and recursive function with the right child node as the new root.

Solution

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func rangeSumBST(root *TreeNode, low int, high int) int {
    if root == nil { return 0 }

    if root.Val < low {
        return rangeSumBST(root.Right, low, high)
    } else if root.Val > high {
        return rangeSumBST(root.Left, low, high)
    } else {
        return root.Val + rangeSumBST(root.Left, low, high) + rangeSumBST(root.Right, low, high)
    }
}

Longest Mountain in Array

You may recall that an array arr is a mountain array if and only if:

arr.length >= 3
There exists some index i (0-indexed) with 0 < i < arr.length - 1 such that:
- arr[0] < arr[1] < ... < arr[i - 1] < arr[i]
- arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

Given an integer array arr, return the length of the longest subarray, which is a mountain. Return 0 if there is no mountain subarray.

Example 1:

Input: arr = [2,1,4,7,3,2,5]
Output: 5
Explanation: The largest mountain is [1,4,7,3,2] which has length 5.

Example 2:

Input: arr = [2,2,2]
Output: 0
Explanation: There is no mountain.

Constraints:

1 <= arr.length <= 10^4
0 <= arr[i] <= 10^4

Follow up:

Can you solve it using only one pass?
Can you solve it in O(1) space?

Explanation 1

To find a length of the mountain, we need to find a peek point such that number of increasing elements end at the peek point, and number of decreasing elements start from the peek point.
We can create two dp arrays. One is up[i] which represents number of increasing elements end at index i. Another one is down[i] which represents number of decreasing elements start from index i. We can use 1 loop to fill the up array, and 1 loop to fill the down array.
The result will be the maximum of up[i] + down[i] + 1.

Solution 1

func longestMountain(arr []int) int {
    res := 0
    up, down := make([]int, len(arr)), make([]int, len(arr))

    for i := 1; i < len(arr); i++ {
        if arr[i] > arr[i-1] {
            up[i] = up[i-1] + 1
        }
    }

    for i := len(arr) - 2; i >= 0; i-- {
        if arr[i] > arr[i+1] {
            down[i] = down[i+1] + 1
        }
        if up[i] > 0 && down[i] > 0 {
            res = max(res, up[i] + down[i] + 1)
        }
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Explanation 2

We can save space by using a variable up to represent the number of increasing elements for the current mountain, and a variable down to represent the number of decreasing elements for the current mountain. We only update the result when both up and down are greater than 0, in other word, res = max(res, up + down + 1).
How do we reset up and down for a new mountain? Each iteration, we first check if down > 0 && A[i-1] < A[i] or A[i-1] == A[i], then we reset both up and down to 0.

Solution 2

func longestMountain(arr []int) int {
    res, up, down := 0, 0, 0
    for i := 1; i < len(arr); i++ {
        if down > 0 && arr[i-1] < arr[i] || arr[i-1] == arr[i] {
            up, down = 0, 0
        }
        if arr[i-1] < arr[i] { up += 1 }
        if arr[i-1] > arr[i] { down += 1 }
        if up > 0 && down > 0 {
            res = max(res, up + down + 1)
        }
    }
    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Mirror Reflection

There is a special square room with mirrors on each of the four walls. Except for the southwest corner, there are receptors on each of the remaining corners, numbered 0, 1, and 2.

The square room has walls of length p, and a laser ray from the southwest corner first meets the east wall at a distance q from the 0th receptor.

Return the number of the receptor that the ray meets first. (It is guaranteed that the ray will meet a receptor eventually.)

Example 1:

Input: p = 2, q = 1
Output: 2
Explanation: The ray meets receptor 2 the first time it gets reflected back to the left wall.

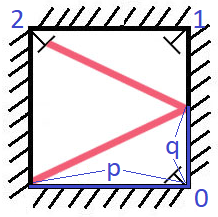
Note:

1 <= p <= 1000
0 <= q <= p

Explanation

This is a brain teaser or math problem.
If p is odd number and q is odd number, then the answer is 1.
If p is odd number and q is even number, then the answer is 0.
If p is even number and q is odd number, then the answer is 2.
There won’t be a case that p and q are both even number. For example, if p = 4 and q = 2, then it is the same as p = 2 and q = 1.

Source: https://www.cnblogs.com/grandyang/p/10646040.html

Solution

func mirrorReflection(p int, q int) int {
    for p % 2 == 0 && q % 2 == 0 {
        p /= 2;
        q /= 2;
    }

    if p % 2 == 0 { return 2; }
    if q % 2 == 0 { return 0; }
    return 1;
}

Merge Intervals

Given an array of intervals where intervals[i] = [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input.

Example 1:

Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].

Example 2:

Input: intervals = [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.

Constraints:

1 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= starti <= endi <= 10^4

Explanation

First, sort the interval by their start time.
To form an interval, we need a start and end. Initially, we initialize start is the first interval’s start time, end is the first interval’s end time.
Loop from the second interval to the end, if the iterated interval’s start time is greater than end, we know they are disjoint. So we add an interval {start, end} to the result list. Then we update start be the iterated interval’s start time, end be the interval’s end time. In the next iteration, if the iterated interva’s start time is less than end, we only need to update end be the maximum of (end, intervals[i][1]), we don’t need to update start because we already sorted start from small to large, and we only need the minimum start and maximum end.

Solution

func merge(intervals [][]int) [][]int {
    if len(intervals) == 1 { return intervals }

    sort.Slice(intervals, func (i, j int) bool {
        return intervals[i][0] < intervals[j][0]
    })
    res := make([][]int, 0)

    start, end := intervals[0][0], intervals[0][1]
    for i := 1; i < len(intervals); i++ {
        curStart, curEnd := intervals[i][0], intervals[i][1]
        if end < curStart {
            res = append(res, []int{start, end})
            start = curStart
            end = curEnd
        } else {
            end = max(end, curEnd)
        }
    }
    res = append(res, []int{start, end})

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Decode String

Given an encoded string, return its decoded string.

The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.

You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.

Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there won’t be input like 3a or 2[4].

Example 1:

Input: s = "3[a]2[bc]"
Output: "aaabcbc"

Example 2:

Input: s = "3[a2[c]]"
Output: "accaccacc"

Example 3:

Input: s = "2[abc]3[cd]ef"
Output: "abcabccdcdcdef"

Example 4:

Input: s = "abc3[cd]xyz"
Output: "abccdcdcdxyz"

Constraints:

1 <= s.length <= 30
s consists of lowercase English letters, digits, and square brackets '[]'.
s is guaranteed to be a valid input.
All the integers in s are in the range [1, 300].

Explanation

We can also solve it using iteration method. First, we create two stacks. numSt and strSt, and a repeat counter cnt.
Then we iterate the string, if the current character is digit, then we update the counter repeat. Else if the current character is not digit and not [ or ], then we add the letter into the result res. If current character is [, then we push the counter into numSt, push res into strSt, and we reset cnt=0 and clear the string res. Else if current character is ], then we pop the numSt to get the counter repeat, and iterate repeat times adding res to the top of the strSt. After that, we pop out the strSt and set it to res.

Solution

func decodeString(s string) string {
    res := ""
    numSt, strSt := make([]int, 0), make([]string, 0)
    cnt := 0

    for i := range s {
        if s[i] >= '0' && s[i] <= '9' {
            cnt = cnt * 10 + int(s[i] - '0')
        } else if s[i] == '[' {
            numSt = append(numSt, cnt)
            strSt = append(strSt, res)
            cnt = 0
            res = ""
        } else if s[i] == ']' {
            repeat := numSt[len(numSt)-1]
            numSt = numSt[:len(numSt)-1]
            sb := strings.Builder{}
            for j := 0; j < repeat; j++ {
                sb.WriteString(res)
            }
            strSt[len(strSt)-1] += sb.String()
            res = strSt[len(strSt)-1]
            strSt = strSt[:len(strSt)-1]
        } else {
            res += string(s[i])
        }
    }

    return res
}

Search in Rotated Sorted Array II

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,0,1,2,2,5,6] might become [2,5,6,0,0,1,2]).

You are given a target value to search. If found in the array return true, otherwise return false.

Example 1:

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2:

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Follow up:

This is a follow up problem to Search in Rotated Sorted Array, where nums may contain duplicates.
Would this affect the run-time complexity? How and why?

Explanation

Similar to 33. Search in Rotated Sorted Array, now, we also need to consider the case that nums[mid] == nums[left] == num[right]. In this case, we can move left one step forward, so the mid will also move forward, until !(nums[mid] == nums[left] == num[right]), and now it is the same as 33. Search in Rotated Sorted Array.

Solution

func search(nums []int, target int) bool {
    if len(nums) == 0 { return false }

    left, right := 0, len(nums) - 1
    for left < right {
        mid := left + (right - left) / 2
        if nums[mid] == target {
            return true
        } else if nums[mid] < nums[left] {
            if target > nums[mid] && target <= nums[right] {
                left = mid + 1
            } else {
                right = mid
            }
        } else if nums[mid] > nums[left] {
            if target >= nums[left] && target < nums[mid] {
                right = mid
            } else {
                left = mid + 1
            }
        } else {
            left += 1
        }
    }

    if nums[left] == target {
        return true
    } else {
        return false
    }
}

Numbers At Most N Given Digit Set

Given an array of digits which is sorted in non-decreasing order. You can write numbers using each digits[i] as many times as we want. For example, if digits = ['1','3','5'], we may write numbers such as '13', '551', and '1351315'.

Return the number of positive integers that can be generated that are less than or equal to a given integer n.

Example 1:

Input: digits = ["1","3","5","7"], n = 100
Output: 20
Explanation:
The 20 numbers that can be written are:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.

Example 2:

Input: digits = ["1","4","9"], n = 1000000000
Output: 29523
Explanation:
We can write 3 one digit numbers, 9 two digit numbers, 27 three digit numbers,
81 four digit numbers, 243 five digit numbers, 729 six digit numbers,
2187 seven digit numbers, 6561 eight digit numbers, and 19683 nine digit numbers.
In total, this is 29523 integers that can be written using the digits array.

Example 3:

Input: digits = ["7"], n = 8
Output: 1

Constraints:

1 <= digits.length <= 9
digits[i].length == 1
digits[i] is a digit from '1' to '9'.
All the values in digits are unique.
digits is sorted in non-decreasing order.
1 <= n <= 10^9

Explanation

If n has 2 digit, then all one digit from digits[] are valid, in other words, res += digits.length. If n has 3 digit, then all two digit from digits[] are also valid, in other words, res += digits.length ^ 2. Therefore, if n has nLen digit, then we can generate all numbers that are 1 to nLen - 1 digits from digits[] are valid.
Now, we need to consider the case that generate all numbers that are nLen digits and less than or equal to n.
For example, if digits = ["1", "3", "9"] and n = 537. First, we compare with n’s first digit 5. From digits[], 1 is less than 5, so we can generate all numbers that start from 1, in other words, res += (nLen - 1 - 0) ^ 2 (ignore the 0 now). Then we check 3 is also less than 5, so we can generate all numbers that start from 3, in other words, res += (nLen - 1 - 0)^2. Then we check 9, which is greater than 5, so we ignore. In this example, we can generate all nLen digit numbers that start from 1 and 3.
One more case is if digits = ["1", "3", "9"] and n = 345. First, we compare with n’s first digit 3. From digits[], 1 is less than 3, so we can generate all numbers that start from 1. Then we compare 3 from digits[] with n’s first digit 3. They are equal, that means we can generate some numbers that start from 3. So now we compare with n’s second digit 4. From digits[], 1 is less than 4, so we can generate all numbers that start from 31, in other words, res += (nLen - 1 - 1)^2. Then we compare 3 from digits[] with 4. 3 is less than 4, so we can generate all numbers that start from 33, in other words, res += (nLen - 1 - 1) ^ 2. Then we compare 9 from digits[] with 4, 9 is greater than 4, so we ignore. At the end, we can generate all nLen digits number that are start from 1, start from 31, and start from 33.
One corner case is if digits = ["1", "1", "1"] and n = 111, then we can only generate one number that are nLen whch is 111 and its less than or equal to n.

Solution

func atMostNGivenDigitSet(digits []string, n int) int {
    res := 0
    str := strconv.Itoa(n)
    nLen := len(str)

    for i := 2; i <= nLen; i++ {
        res += int(math.Pow(float64(len(digits)), float64(i-1)))
    }

    for i := 0; i < nLen; i++ {
        hasSameNum := false
        for _, digit := range digits {
            if digit[0] < str[i] {
                res += int(math.Pow(float64(len(digits)), float64(nLen - 1 - i)))
            } else if digit[0] == str[i] {
                hasSameNum = true
            }
        }
        if hasSameNum == false { return res }
    }

    return res + 1
}

Week 4: November 22nd - November 28th

Longest Substring with At Most Two Distinct Characters

Given a string s , find the length of the longest substring t that contains at most 2 distinct characters.

Example 1:

Input: "eceba"
Output: 3
Explanation: t is "ece" which its length is 3.

Example 2:

Input: "ccaabbb"
Output: 5
Explanation: t is "aabbb" which its length is 5.

Explanation 1

First, we can create a HashMap, and use it to store the key is the character, the value is the frequency of the character. Also, we initialize the left be 0. Iterate the input string and update the hashmap. While the hashmap has size greater than 2, then we need to decrease the frequency of character s[left] and increase left by 1. Also if the s[left]’s frequency is 0, we remove the key s[left] from the hashmap. Repeat these steps until the hashmap has size less than or equal to 2. Next, we update the result be max(res, i-left+1).

Solution 1

class Solution {
    public int lengthOfLongestSubstringTwoDistinct(String s) {
        int res = 0;
        int left = 0;
        Map<Character, Integer> hm = new HashMap<>();

        for (int i = 0; i < s.length(); i++) {
            char curChar = s.charAt(i);
            hm.put(curChar, hm.getOrDefault(curChar, 0)+1);
            while (hm.size() > 2) {
                char leftChar = s.charAt(left);
                hm.put(leftChar, hm.get(leftChar)-1);
                if (hm.get(leftChar) == 0) hm.remove(leftChar);
                left += 1;
            }

            res = Math.max(res, i-left+1);
        }

        return res;
    }
}

Explanation 2

We can optimize the last solution by not using HashMap. First, we create two variables first means the first distince character, second means the second distince character. Also, we initialize curLen means the current 2 distinct character substring’s length, and cntSecond means the number of consecutive second characters.
Iterate the input string’s characters. If the current character is the same as either character first or character second, we update curLen = curLen + 1, else, we update curLen = cntSecond + 1.
Then, we try to update cntSecond. If the current character is the same as character second, then cntSecond = cntSecond + 1, else cntSecond = 1.
Next, we try to update first and second. If the current character is not the same as second, then we update first be the original second and second be the current character.
Next, we update the result res = max(res, curLen).

Solution 2

class Solution {
    public int lengthOfLongestSubstringTwoDistinct(String s) {
        int res = 0;
        int curLen = 0, cntSecond = 0;
        char first = ' ';
        char second = ' ';

        for (char c: s.toCharArray()) {
            curLen = (c == first || c == second) ? curLen + 1 : cntSecond + 1;
            cntSecond = (c == second) ? cntSecond + 1 : 1;
            if (c != second) {
                first = second;
                second = c;
            }
            res = Math.max(res, curLen);
        }

        return res;
    }
}

Unique Morse Code Words

International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows: "a" maps to ".-", "b" maps to "-...", "c" maps to "-.-.", and so on.

For convenience, the full table for the 26 letters of the English alphabet is given below:

[".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."]

Now, given a list of words, each word can be written as a concatenation of the Morse code of each letter. For example, “cab” can be written as “-.-..–…”, (which is the concatenation “-.-.” + “.-“ + “-...”). We’ll call such a concatenation, the transformation of a word.

Return the number of different transformations among all words we have.

Example:
Input: words = ["gin", "zen", "gig", "msg"]
Output: 2
Explanation:
The transformation of each word is:
"gin" -> "--...-."
"zen" -> "--...-."
"gig" -> "--...--."
"msg" -> "--...--."

There are 2 different transformations, "--...-." and "--...--.".

Note:

The length of words will be at most 100.
Each words[i] will have length in range [1, 12].
words[i] will only consist of lowercase letters.

Explanation

We can use brute force to solve this problem.
First, we find all words’ morse code, then put them into a set. At the end, we can return the size of the set.

Solution

func uniqueMorseRepresentations(words []string) int {
    set := make(map[string]bool)
    dict := []string{".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."}

    for i := range words {
        morse := ""
        for j := range words[i] {
            morse += dict[words[i][j] - 'a']
        }
        set[morse] = true
    }

    return len(set)
}

House Robber III

The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the “root.” Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that “all houses in this place forms a binary tree”. It will automatically contact the police if two directly-linked houses were broken into on the same night.

Determine the maximum amount of money the thief can rob tonight without alerting the police.

Example 1:

Input: [3,2,3,null,3,null,1]

     3
    / \
   2   3
    \   \
     3   1

Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.

Example 2:

Input: [3,4,5,1,3,null,1]

     3
    / \
   4   5
  / \   \
 1   3   1

Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.

Explanation

For Tree problem, we usually use recursive method to solve. The thief can have only two options.
1. Get the root val, don’t get root.left.val and root.right.val, but get root.left.left.val, root.left.right.val, and root.right.left.val, root.right.right.val.
2. Don’t get the root val, but get root.left.val and root.right.val.
The base case is if root is NULL, we return 0.
We can use a HashMap hm<TreeNode, Integer> to store the maximum the thieft can get on root. Think of the tree is made by many root.

Solution

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func rob(root *TreeNode) int {
    hm := make(map[*TreeNode]int)
    return helper(root, hm)
}

func helper(root *TreeNode, hm map[*TreeNode]int) int {
    if root == nil { return 0 }
    if _, ok := hm[root]; ok {
        return hm[root]
    }

    res := root.Val
    if root.Left != nil {
        res += helper(root.Left.Left, hm)
        res += helper(root.Left.Right, hm)
    }
    if root.Right != nil {
        res += helper(root.Right.Left, hm)
        res += helper(root.Right.Right, hm)
    }

    res = max(res, helper(root.Left, hm) + helper(root.Right, hm))
    hm[root] = res

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Basic Calculator II

Given a string s which represents an expression, evaluate this expression and return its value.

The integer division should truncate toward zero.

Example 1:

Input: s = "3+2*2"
Output: 7

Example 2:

Input: s = " 3/2 "
Output: 1

Example 3:

Input: s = " 3+5 / 2 "
Output: 5

Constraints:

1 <= s.length <= 3 * 10^5
s consists of integers and operators ('+', '-', '*', '/') separated by some number of spaces.
s represents a valid expression.

All the integers in the expression are non-negative integers in the range [0, 2^31 - 1].

The answer is guaranteed to fit in a 32-bit integer.

Explanation

Before we begin, we need to have a preSign initialize to +, a stack to hold the sub result.
Iterate the string, if the current character is a number, then we update the number be num = num*10+c. If the current character is not a number, then check if the preSign is plus, we push the num to stack; if the preSign is minus, then we push -num to stack; if the preSign is multiple, then we pop the stack’s number and multiple to num and store this sub result back to stack; if the preSign is divide, it’s similar to multiple, but divide the num and push back to stack. Also remember to update the preSign equal to current character, and reset num to 0.
Sum all sub result from stack and return it as result.

Solution

func calculate(s string) int {
    st := make([]int, 0)
    res, num := 0, 0
    preSign := '+'

    for i, c := range s {
        if c >= '0' {
            num = num * 10 + int(c - '0')
        }
        if c < '0' && c != ' ' || i == len(s) - 1 {
            if preSign == '+' { st = append(st, num) }
            if preSign == '-' { st = append(st, -num) }
            if preSign == '*' {
                temp := st[len(st)-1]
                st = st[:len(st)-1]
                st = append(st, temp * num)
            }
            if preSign == '/' {
                temp := st[len(st)-1]
                st = st[:len(st)-1]
                st = append(st, temp / num)
            }
            preSign = c
            num = 0
        }
    }

    for i := range st {
        res += st[i]
    }

    return res
}

Smallest Integer Divisible by K

Given a positive integer K, you need to find the length of the smallest positive integer N such that N is divisible by K, and N only contains the digit 1.

Return the length of N. If there is no such N, return -1.

Note: N may not fit in a 64-bit signed integer.

Example 1:

Input: K = 1
Output: 1
Explanation: The smallest answer is N = 1, which has length 1.

Example 2:

Input: K = 2
Output: -1
Explanation: There is no such positive integer N divisible by 2.

Example 3:

Input: K = 3
Output: 3
Explanation: The smallest answer is N = 111, which has length 3.

Constraints:

1 <= K <= 10^5

Hint 1:

11111 = 1111 * 10 + 1 We only need to store remainders modulo K.

Hint 2:

If we never get a remainder of 0, why would that happen, and how would we know that?

Explanation

This is a math problem and there is a formula to solve this problem.

Solution

func smallestRepunitDivByK(K int) int {
    if K % 2 == 0 || K % 5 == 0 { return -1 }

    g := 0
    for i := 1; i <= K; i++ {
        g = (g * 10 + 1) % K
        if g == 0 { return i }
    }

    return -1
}

Longest Substring with At Least K Repeating Characters

Given a string s and an integer k, return the length of the longest substring of s such that the frequency of each character in this substring is greater than or equal to k.

Example 1:

Input: s = "aaabb", k = 3
Output: 3
Explanation: The longest substring is "aaa", as 'a' is repeated 3 times.

Example 2:

Input: s = "ababbc", k = 2
Output: 5
Explanation: The longest substring is "ababb", as 'a' is repeated 2 times and 'b' is repeated 3 times.

Constraints:

1 <= s.length <= 10^4
s consists of only lowercase English letters.
1 <= k <= 10^5

Explanation

We can use DFS to solve this problem. First, we get the frequency of characters into a HashMap freq. Also, we loop through the freq’s key set, if the current character’s frequency is less than k, then we store the current character into a set splitSet. The base case is if the splitSet is empty, that means all characters in the input string have frequency equals or greater than k, so the maximum length will be the full length of s.
Next, we create two variables start and cur both initialize to 0. We loop through the string with cur, if s[cur] is not in the splitSet, then we continue for the next iteration. Else if s[cur] is in the splitSet, that means s[cur] cannot be stored into the result, so we recursivly check the result length with substring s[start, cur], and compare the returned result length with variable max that keeps the maximum result length. Then, we update start = cur + 1 since cur is pointing to the character that cannot be put into the result string.
When outside the loop, if start and cur not equals, we need to pass the last substring s[start, len(s)] to the recursive method and compare its result with max. At the end, we return max.

Solution

func longestSubstring(s string, k int) int {
    hm := make(map[byte]int)
    for i := range s {
        hm[s[i]] += 1
    }

    splitSet := make(map[byte]bool)
    for ch,v := range hm {
        if v < k {
            splitSet[ch] = true
        }
    }

    if len(splitSet) == 0 { return len(s) }

    res := 0
    start, cur := 0, 0

    for cur < len(s) {
        if splitSet[s[cur]] == true {
            res = max(res, longestSubstring(s[start:cur], k))
            start = cur + 1
        }
        cur += 1
    }

    if start != cur {
        res = max(res, longestSubstring(s[start:cur], k))
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Partition Equal Subset Sum

Given a non-empty array nums containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Example 1:

Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.

Constraints:

1 <= nums.length <= 200
1 <= nums[i] <= 100

Explanation

Since we want two subsets have the same sum, so the input array’s total sum must be an even number, and both subset must have the target sum equals to totalSum/2.
We can use dynamic programming to solve this problem. Dynamic state is boolean dp[i] and i is between 0 to target inclusive. If dp[i] is true, that means we can choose some numbers from the input array and sum to i.
Dynamic init is dp[0] = true.
Dynamic function. For each number in the array, we loop i from target to that number, dp[i] will be true if dp[i - num] is true. For example, if array is [1, 5, 11, 5], when we iterate to num = 5. dp[i = 6] will be true because dp[6-5] = dp[1] = true, and dp[i = 5] will be true because dp[5 - 5] = dp[0] = true. Also, if dp[i] is already true, we keep it as true. Therefore, we have dp[i] = dp[i] || dp[i - num].
Dynamic result is return dp[target].

Solution

func canPartition(nums []int) bool {
    sum := 0
    for _, num := range nums {
        sum += num
    }
    if sum % 2 != 0 { return false }

    target := sum / 2
    dp := make([]bool, target+1)
    dp[0] = true

    for _, num := range nums {
        for t := target; t >= num; t-- {
            dp[t] = dp[t] || dp[t - num]
        }
    }

    return dp[target]
}

Sliding Window Maximum

You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.

Return the max sliding window.

Example 1:

Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
Output: [3,3,5,5,6,7]
Explanation:
Window position                Max
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

Example 2:

Input: nums = [1], k = 1
Output: [1]

Example 3:

Input: nums = [1,-1], k = 1
Output: [1,-1]

Example 4:

Input: nums = [9,11], k = 2
Output: [11]

Example 5:

Input: nums = [4,-2], k = 2
Output: [4]

Constraints:

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length

Hint 1:

How about using a data structure such as deque (double-ended queue)?

Hint 2:

The queue size need not be the same as the window’s size.

Hint 3:

Remove redundant elements and the queue should store only elements that need to be considered.

Explanation

We can use a deque to store the index of element, and the deque is sorted from highest to lowest.
Iterate the array, if the queue is empty, then we insert the current index to the deque. Else, while the number value on the current index is greater than the tail value of the deque, we pop it. Outside of the while loop, we insert the current index to the deque. So, the deque is sorted descendent.
If the current index is greater than or equal to k-1, then a window is created, and we add the value num[head of the deque] to the result array.
If the head of the deque is equal to currentIndex - k, that means the head index is outside of the window, so we remove the head.

Solution

func maxSlidingWindow(nums []int, k int) []int {
    res := make([]int, len(nums) - k + 1)
    queue := make([]int, 0)

    for i := 0; i < len(nums); i++ {
        if len(queue) > 0 && i-k == queue[0] {
            queue = queue[1:]
        }
        for len(queue) > 0 && nums[i] > nums[queue[len(queue)-1]] {
            queue = queue[:len(queue)-1]
        }
        queue = append(queue, i)
        if i >= k-1 {
            res[i-(k-1)] = nums[queue[0]]
        }
    }

    return res
}

Week 5: November 29th - November 30th

Maximum Average Subarray II

You are given an integer array nums consisting of n elements, and an integer k.

Find a contiguous subarray whose length is greater than or equal to k that has the maximum average value and return this value. Any answer with a calculation error less than 10^-5 will be accepted.

Example 1:

Input: nums = [1,12,-5,-6,50,3], k = 4
Output: 12.75000
Explanation:
- When the length is 4, averages are [0.5, 12.75, 10.5] and the maximum average is 12.75
- When the length is 5, averages are [10.4, 10.8] and the maximum average is 10.8
- When the length is 6, averages are [9.16667] and the maximum average is 9.16667
The maximum average is when we choose a subarray of length 4 (i.e., the sub array [12, -5, -6, 50]) which has the max average 12.75, so we return 12.75
Note that we do not consider the subarrays of length < 4.

Example 2:

Input: nums = [5], k = 1
Output: 5.00000

Constraints:

n == nums.length
1 <= k <= n <= 10^4
-10^4 <= nums[i] <= 10^4

Explanation 1

We can use brute force to solve this problem, but it will TLE.
Loop i from the beginning of the array to n-k inclusive, and i represent the starting index of the subarray that has length at least k. Inside the loop, we try to extend the subarray, so we create an inner loop that loop j from i to the last index of the array, and j represent the ending index of the subarray. Inside this inner loop, we check if the length of the subarray has size equal or greater than k, then we calculate its average and update the result to get the maximum of the average.

Solution 1

class Solution {
    public double findMaxAverage(int[] nums, int k) {
        int n = nums.length;
        double res = Integer.MIN_VALUE;

        for (int i = 0; i <= n - k; i++) {
            long sum = 0;
            for (int j = i; j < n; j++) {
                sum += nums[j];
                if (j - i + 1 >= k) {
                    res = Math.max(res, sum * 1.0 / (j - i + 1));
                }
            }
        }

        return res;
    }
}

Explanation 2

We can use binary search to solve this problem.
First, we know that the value of the average could lie between the range (min,max). Here, min and max refer to the minimum and the maximum values out of the given nums array. This is because, the average can’t be lesser than the minimum value and can’t be larger than the maximum value.
We will use the mid as our guessing result.
Suppose, there exist j elements, a1,a2,a3…,aj in a subarray within nums such that their average is greater than mid. In this case, we can say that
- (a_1+a_2+ a_3…+a_j)/j ≥ mid or
- (a_1+a_2+ a_3…+a_j) ≥ j*mid or
- (a_1-mid) +(a_2-mid)+ (a_3-mid) …+(a_j-mid) ≥ 0
The check function will return true if there’s a subarray that has length at least k and its average is equal or greater than mid.

Solution 2

class Solution {
    boolean check(int[] nums, int k, double mid) {
        double curSum = 0;
        double prevSum = 0;
        double minSum = 0;

        for (int i = 0; i < nums.length; i++) {
            curSum += nums[i] - mid;
            if (i >= k - 1) {
                if (curSum - minSum >= 0) return true;
                prevSum += nums[i + 1 - k] - mid;
                minSum = Math.min(minSum, prevSum);
            }
        }

        return false;
    }

    public double findMaxAverage(int[] nums, int k) {
        double left = nums[0];
        double right = nums[0];

        for (int num: nums) {
            left = Math.min(left, num);
            right = Math.max(right, num);
        }

        while (right - left > 1e-5) {
            double mid = left + (right - left) / 2;
            if (check(nums, k, mid)) {
                left = mid;
            } else {
                right = mid;
            }
        }

        return left;
    }
}

Jump Game III

Given an array of non-negative integers arr, you are initially positioned at start index of the array. When you are at index i, you can jump to i + arr[i] or i - arr[i], check if you can reach to any index with value 0.

Notice that you can not jump outside of the array at any time.

Example 1:

Input: arr = [4,2,3,0,3,1,2], start = 5
Output: true
Explanation:
All possible ways to reach at index 3 with value 0 are:
index 5 -> index 4 -> index 1 -> index 3
index 5 -> index 6 -> index 4 -> index 1 -> index 3

Example 2:

Input: arr = [4,2,3,0,3,1,2], start = 0
Output: true
Explanation:
One possible way to reach at index 3 with value 0 is:
index 0 -> index 4 -> index 1 -> index 3

Example 3:

Input: arr = [3,0,2,1,2], start = 2
Output: false
Explanation: There is no way to reach at index 1 with value 0.

Constraints:

1 <= arr.length <= 5 * 10^4
0 <= arr[i] < arr.length
0 <= start < arr.length

Hint 1:

Think of BFS to solve the problem.

Hint 2:

When you reach a position with a value = 0 then return true.

Explanation

Start from index start, we first check if arr[start] equals to 0, if it is, then we return true immediately. Else, we check arr[start - arr[start]] and arr[start + arr[start]]. We can use BFS to check all possible routes. If an index is already checked, we do not need to check it again, we can achieve this by marking the visited index’s value as negative arr[curIdx] = -1.

Solution

func canReach(arr []int, start int) bool {
    queue := make([]int, 0)
    queue = append(queue, start)

    for len(queue) > 0 {
        curIdx := queue[0]
        queue = queue[1:]
        if arr[curIdx] == 0 { return true }
        if arr[curIdx] == -1 { continue }

        if curIdx + arr[curIdx] < len(arr) {
            queue = append(queue, curIdx + arr[curIdx])
        }

        if curIdx - arr[curIdx] >= 0 {
            queue = append(queue, curIdx - arr[curIdx])
        }

        arr[curIdx] = -1
    }

    return false
}

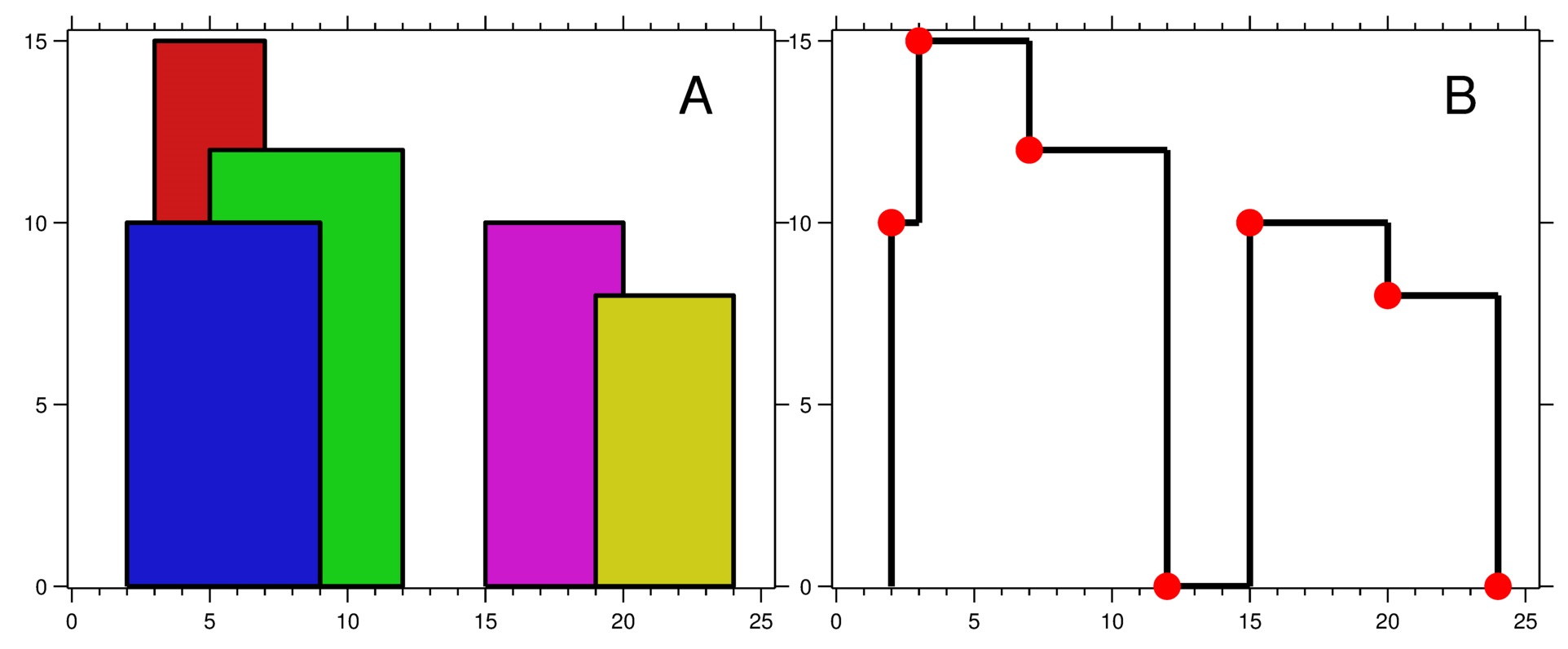
The Skyline Problem

A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Given the locations and heights of all the buildings, return the skyline formed by these buildings collectively.

The geometric information of each building is given in the array buildings where buildings[i] = [lefti, righti, heighti]:

left_i is the x coordinate of the left edge of the ith building.
right_i is the x coordinate of the right edge of the ith building.
height_i is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of “key points” sorted by their x-coordinate in the form [[x1,y1],[x2,y2],...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline’s termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline’s contour.

Note: There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3],[4 5],[7 5],[11 5],[12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...,[2 3],[4 5],[12 7],...]

Example 1:

Input: buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
Output: [[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
Explanation:
Figure A shows the buildings of the input.
Figure B shows the skyline formed by those buildings. The red points in figure B represent the key points in the output list.

Example 2:

Input: buildings = [[0,2,3],[2,5,3]]
Output: [[0,3],[5,0]]

Constraints:

1 <= buildings.length <= 10^4
0 <= lefti < righti <= 2^31 - 1
1 <= height_i <= 2^31 - 1
buildings is sorted by left_i in non-decreasing order.

Explanation

First, store every column edge int[x, y] into a list height which is sorted by the edge’s x position, if two edge has the same x position, then higher edge, in other words, higher y in front. Note, a rectangle’s start column edge will be both positive x and y, ending edge will be positive x but negative height y. In other words, <start, height> and <end, -height>.
We also need a priority queue to store the integer height, and the queue is sorted by higher height in front. Also, the queue will be inserted a 0 first, and we need a cur and pre to record the pop height from the queue later.
Iterate the list height<int[]>, if the edge’s y position is positive, then we enqueue the y; else, remove the negative y from the queue, in other words, remove the begin edge’s y from the queue. Then, we update the cur height be the peek of the queue, and check if cur is different from pre, then we get the skinline key point as the iterative edge’s x position as the key point’s x position, key point’s y position will be cur which is the peek height of the queue. After we insert the keypoint to the result list, we update the pre equal to cur.

Solution

func getSkyline(buildings [][]int) [][]int {
    res := make([][]int, 0)

    height := make([][]int, 0)
    for i := range buildings {
        height = append(height, []int{buildings[i][0], buildings[i][2]})
        height = append(height, []int{buildings[i][1], -buildings[i][2]})
    }
    sort.Slice(height, func(i, j int) bool {
        if height[i][0] == height[j][0] {
            return height[i][1] > height[j][1]
        } else {
            return height[i][0] < height[j][0]
        }
    })

    queue := &IntHeap{0}
	heap.Init(queue)

    cur, pre := 0, 0
    for _, h := range height {
        if h[1] > 0 {
            heap.Push(queue, h[1])
        } else {
            queue.Remove(-h[1])
            heap.Init(queue)
        }

        cur = (*queue)[0]

        if pre != cur {
            res = append(res, []int{h[0], cur})
            pre = cur
        }
    }

    return res
}


type IntHeap []int

func (h IntHeap) Len() int           { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] > h[j] }
func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IntHeap) Push(x interface{}) {
	// Push and Pop use pointer receivers because they modify the slice's length,
	// not just its contents.
	*h = append(*h, x.(int))
}

func (h *IntHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

func (h *IntHeap) Remove(toRemove int) {
    old := *h
    for i := range old {
        if old[i] == toRemove {
            old[i], old[len(old)-1] = old[len(old)-1], old[i]
            *h = old[0: len(old)-1]
            break
        }
    }
}