October LeetCoding Challenge

Posted on | In

It’s been half year since doing LeetCoding Challenge! Let’s continue October LeetCoding Challenge.

Week 1: October 1st - October 7th

Maximum Distance in Arrays

Given m arrays, and each array is sorted in ascending order. Now you can pick up two integers from two different arrays (each array picks one) and calculate the distance. We define the distance between two integers a and b to be their absolute difference |a-b|. Your task is to find the maximum distance.

Example 1:

1
2
3
4
5
6
7
Input:
[[1,2,3],
 [4,5],
 [1,2,3]]
Output: 4
Explanation:
One way to reach the maximum distance 4 is to pick 1 in the first or third array and pick 5 in the second array.

Note:

  1. Each given array will have at least 1 number. There will be at least two non-empty arrays.

  2. The total number of the integers in all the m arrays will be in the range of [2, 10000].

  3. The integers in the m arrays will be in the range of [-10000, 10000].

Explanation 1

  1. Since each array is sorted, we can get the minimum element and maximum element easily, then the result will be the maximum element subtract the minimum element.

  2. Since we can’t get both the minimum and maximum element from the same array, we need to to record both the element and its index. We can solve this problem using a minHeap and a maxHeap. Both heaps will store the pair of element and its index. MinHeap will store the each array’s first element and the array index, maxHeap will store each array’s last element and the array index.

  3. After looping all arrays and build up the minHeap and maxHeap. We compare the top of both heaps to check if both pair element are from the same array index. If they are, then we return the max between max(max - secondMin, secondMax - min). Else, we can just return maxHeap’s top element subtract minHeap’s top element.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int maxDistance(List<List<Integer>> arrays) {
        Queue<int[]> minHeap = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        Queue<int[]> maxHeap = new PriorityQueue<>((a, b) -> b[0] - a[0]);

        for (int i = 0; i < arrays.size(); i++) {
            List<Integer> arr = arrays.get(i);
            int curMin = arr.get(0);
            int curMax = arr.get(arr.size()-1);
            minHeap.offer(new int[]{curMin, i});
            maxHeap.offer(new int[]{curMax, i});
        }

        if (minHeap.peek()[1] == maxHeap.peek()[1]) {
            int min = minHeap.poll()[0];
            int max = maxHeap.poll()[0];
            int secondMin = minHeap.poll()[0];
            int secondMax = maxHeap.poll()[0];
            return Math.max(max - secondMin, secondMax - min);
        }

        return maxHeap.poll()[0] - minHeap.poll()[0];
    }
}

Explanation 2

  1. Since we can’t pick max and min from the same array, in other words, max and min must from different arrays. Before we hit the current array, we need to keep track of the preMax and preMin. Then when we are in the current array, we can calculate the result be res = max(res, abs(preMax - curMin), abs(curMax - preMin))), then update preMin and preMax as the minimum element and maximum element we have seen so far.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int maxDistance(List<List<Integer>> arrays) {
        List<Integer> firstArr = arrays.get(0);
        int preMin = firstArr.get(0);
        int preMax = firstArr.get(firstArr.size()-1);
        int res = 0;

        for (int i = 1; i < arrays.size(); i++) {
            List<Integer> arr = arrays.get(i);
            int curMin = arr.get(0);
            int curMax = arr.get(arr.size()-1);
            res = Math.max(res, Math.max(Math.abs(preMax - curMin), Math.abs(curMax - preMin)));
            preMin = Math.min(preMin, curMin);
            preMax = Math.max(preMax, curMax);
        }

        return res;
    }
}

Number of Recent Calls

You have a RecentCounter class which counts the number of recent requests within a certain time frame.

Implement the RecentCounter class:

  • RecentCounter() Initializes the counter with zero recent requests.

  • int ping(int t) Adds a new request at time t, where t represents some time in milliseconds, and returns the number of requests that has happened in the past 3000 milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range [t - 3000, t].

It is guaranteed that every call to ping uses a strictly larger value of t than the previous call.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
Input
["RecentCounter", "ping", "ping", "ping", "ping"]
[[], [1], [100], [3001], [3002]]
Output
[null, 1, 2, 3, 3]

Explanation
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1);     // requests = [1], range is [-2999,1], return 1
recentCounter.ping(100);   // requests = [1, 100], range is [-2900,100], return 2
recentCounter.ping(3001);  // requests = [1, 100, 3001], range is [1,3001], return 3
recentCounter.ping(3002);  // requests = [1, 100, 3001, 3002], range is [2,3002], return 3

Constraints:

  • 1 <= t <= 10^9

  • Each test case will call ping with strictly increasing values of t.

  • At most 10^4 calls will be made to ping.

Explanation

  1. We need to keep track of the number of request in the past 3000 millseconds, we can use a queue to do this.

  2. In the constructor method, we initialize the queue and also the counter.

  3. In the ping method, first increase the counter and append the t into the queue. While q[0] < t - 3000, we poll from the queue and decrease the counter. At the end, the queue will only contain the past 3000 millseconds ping request, we can return its length or the counter.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
type RecentCounter struct {
    queue []int
    cnt int
}


func Constructor() RecentCounter {
    return RecentCounter{[]int{}, 0}
}


func (this *RecentCounter) Ping(t int) int {
    this.queue = append(this.queue, t)
    this.cnt += 1

    for this.queue[0] < t - 3000 {
        this.queue = this.queue[1:]
        this.cnt -= 1
    }

    return this.cnt
}


/**
 * Your RecentCounter object will be instantiated and called as such:
 * obj := Constructor();
 * param_1 := obj.Ping(t);
 */

Combination Sum

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

Example 1:

1
2
3
4
5
6
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2:

1
2
Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3:

1
2
Input: candidates = [2], target = 1
Output: []

Example 4:

1
2
Input: candidates = [1], target = 1
Output: [[1]]

Example 5:

1
2
Input: candidates = [1], target = 2
Output: [[1,1]]

Constraints:

  • 1 <= candidates.length <= 30

  • 1 <= candidates[i] <= 200

  • All elements of candidates are distinct.

  • 1 <= target <= 500

Explanation 1

  1. We can use recursion to solve this problem.

  2. First, we create a result list and a sub temporary sublist, passing these two lists as the parameters to the helper function. Also, we pass the start index initialize to 0 to the helper function. The start index is used to avoid duplicate sublist. For example, if condidates=[1, 2, 3], then if we already push the sublist [1, 2] into the result list, then we don’t want to put [2, 1] into the result list. In other words, after we finding out all the sublist that starts with 1, we then need to find out all the sublist that starts with 2.

  3. The base case if target == 0, we push the sublist into the result list, and return. If the target < 0, we just return.

  4. Note, when we push the temporary sublist into the result list, we will pass the new object of temporary sublist, not the reference of original temporary sublist since it will change everytime.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func combinationSum(candidates []int, target int) [][]int {
    res := make([][]int, 0)
    if candidates == nil || len(candidates) == 0 { return res }
    cur := make([]int, 0)
    sort.Ints(candidates)
    helper(candidates, target, &res, cur, 0)
    return res
}

func helper(candidates []int, target int, res *[][]int, cur []int, start int) {

    if target == 0 {
        temp := append([]int{}, cur...)
        *res = append(*res, temp)
        return
    }
    for i := start; i < len(candidates); i++ {
        if candidates[i] > target {
            break
        } else {
            cur = append(cur, candidates[i])
            helper(candidates, target - candidates[i], res, cur, i)
            cur = cur[:len(cur)-1]
        }
    }
}

Explanation 2

  1. We can also solve this problem using dynamic programming. Let’s use the problem’s Example 1. We first create a dp array dp[] and dp[t] represents all the combinations for target t.

  2. Loop through all the candidates, for each candidate c, inner loop through target t from 1 to target inclusive. If c > t, we can skip. Else if c == t, we find one combination for target t, which is [c], so we append this combination to dp[t]. Else if c < t, assume c is part of the combination, then we need to find all the combinations for dp[t - c], and for each combination, we append c to it, now this combination become the combination for dp[t].

1
2
3
4
5
    0       1       2       3      4       5      6       7
2   -       -      [2]      -    [2, 2]    -   [2,2,2]    -
3   -       -       -      [3]     -       -     [3,3]  [2, 2, 3]
6   -       -       -       -      -       -     [6]      -
7   -       -       -       -      -       -      -      [7]

Solution 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func combinationSum(candidates []int, target int) [][]int {
    dp := make([][][]int, target + 1)

    for _, c := range candidates {
        for t := 1; t <= target; t++ {
            if c > t {
                continue
            } else if c == t {
                dp[t] = append(dp[t], []int{c})
            } else {
                for _, lst := range dp[t - c] {
                    sub := make([]int, len(lst))
                    copy(sub, lst)
                    sub = append(sub, c)
                    dp[t] = append(dp[t], sub)
                }
            }
        }
    }

    return dp[target]
}

K-diff Pairs in an Array

Given an array of integers nums and an integer k, return the number of unique k-diff pairs in the array.

A k-diff pair is an integer pair (nums[i], nums[j]), where the following are true:

  • 0 <= i, j < nums.length

  • i != j

  • a <= b

  • b - a == k

Example 1:

1
2
3
4
Input: nums = [3,1,4,1,5], k = 2
Output: 2
Explanation: There are two 2-diff pairs in the array, (1, 3) and (3, 5).
Although we have two 1s in the input, we should only return the number of unique pairs.

Example 2:

1
2
3
Input: nums = [1,2,3,4,5], k = 1
Output: 4
Explanation: There are four 1-diff pairs in the array, (1, 2), (2, 3), (3, 4) and (4, 5).

Example 3:

1
2
3
Input: nums = [1,3,1,5,4], k = 0
Output: 1
Explanation: There is one 0-diff pair in the array, (1, 1).

Example 4:

1
2
Input: nums = [1,2,4,4,3,3,0,9,2,3], k = 3
Output: 2

Example 5:

1
2
Input: nums = [-1,-2,-3], k = 1
Output: 2

Constraints:

  • 1 <= nums.length <= 10^4

  • -10^7 <= nums[i] <= 10^7

  • 0 <= k <= 10^7

Explanation

  1. First, we put all numbers and their frequency into a hash map.

  2. We want to find two numbers’ difference is k, so if one number plus k and its sum is inside the hashmap, then we increase the result. So we iterate through the hashmap’s key set. For every key, we check if key + k is inside the hashmap, if true, we increase the result by 1.

  3. If k is zero, then for every iterated key, we check its frequency. If the current key’s frequency is greater than 1, we increase the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func findPairs(nums []int, k int) int {
    res := 0
    hm := make(map[int]int)
    for _, num := range nums {
        hm[num] += 1
    }

    for num := range hm {
        if hm[num + k] > 0 {
            if k > 0 {
                res += 1
            } else if k == 0 {
                if hm[num] > 1 { res += 1 }
            }
        }
    }

    return res
}

Remove Covered Intervals

Given a list of intervals, remove all intervals that are covered by another interval in the list.

Interval [a,b) is covered by interval [c,d) if and only if c <= a and b <= d.

After doing so, return the number of remaining intervals.

Example 1:

1
2
3
Input: intervals = [[1,4],[3,6],[2,8]]
Output: 2
Explanation: Interval [3,6] is covered by [2,8], therefore it is removed.

Example 2:

1
2
Input: intervals = [[1,4],[2,3]]
Output: 1

Example 3:

1
2
Input: intervals = [[0,10],[5,12]]
Output: 2

Example 4:

1
2
Input: intervals = [[3,10],[4,10],[5,11]]
Output: 2

Example 5:

1
2
Input: intervals = [[1,2],[1,4],[3,4]]
Output: 1

Constraints:

  1. 1 <= intervals.length <= 1000

  2. intervals[i].length == 2

  3. 0 <= intervals[i][0] < intervals[i][1] <= 10^5

  4. All the intervals are unique.

Hint 1:

How to check if an interval is covered by another?

Hint 2:

Compare each interval to all others and check if it is covered by any interval.

Explanation

  1. For interval problems, we often first sort all intervals by their start or left point.

  2. We have two cases for overlap.

    1
    2
     -------
 --------------------

    1
    2
     --------------------
 -------

  3. We initialize the first interval as the pre-interval and its start and end as preLeft and preRight, and initialize the result res to 1. Loop from the second interval to the last interval. Each iteration, check if the pre-interval with current iterated interval are overlap or not. If overlap, result res increase by 1. Next, update the pre-interval be the interval that has the largest ending point.

  4. After looping all intervals, we return the result res.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func removeCoveredIntervals(intervals [][]int) int {
    sort.Slice(intervals, func (i, j int) bool {
        if intervals[i][0] == intervals[j][0] {
            return intervals[i][1] < intervals[j][1]
        } else {
            return intervals[i][0] < intervals[j][0]
        }
    })

    res := 1
    preLeft, preRight := intervals[0][0], intervals[0][1]

    for _, cur := range intervals {
        curLeft, curRight := cur[0], cur[1]
        if isOverlap(preLeft, preRight, curLeft, curRight) == false {
            res += 1
        }
        if curRight >= preRight {
            preRight = curRight
            preLeft = curLeft
        }
    }

    return res
}

func isOverlap(preLeft, preRight, curLeft, curRight int) bool {
    if preLeft <= curLeft && preRight >= curRight { return true }
    if curLeft <= preLeft && curRight >= preRight { return true }
    return false
}

Complement of Base 10 Integer

Every non-negative integer N has a binary representation. For example, 5 can be represented as "101" in binary, 11 as "1011" in binary, and so on. Note that except for N = 0, there are no leading zeroes in any binary representation.

The complement of a binary representation is the number in binary you get when changing every 1 to a 0 and 0 to a 1. For example, the complement of "101" in binary is "010" in binary.

For a given number N in base-10, return the complement of it’s binary representation as a base-10 integer.

Example 1:

1
2
3
Input: 5
Output: 2
Explanation: 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10.

Example 2:

1
2
3
Input: 7
Output: 0
Explanation: 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10.

Example 3:

1
2
3
Input: 10
Output: 5
Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.

Note:

  1. 0 <= N < 10^9

  2. This question is the same as 476: https://leetcode.com/problems/number-complement/

Hint 1:

A binary number plus its complement will equal 111….111 in binary. Also, N = 0 is a corner case.

Explanation

  1. In order to make 101 becomes 010, we can just do 101 ^ 111 = 010. Similarlly, 111 ^ 111 = 000, and 1010 ^ 1111 = 0101.

  2. From the above example, we know that we first need to find the smallest number a that has all bits set to 1 and a <= N. Initially, we define a = 1, while a < N, then we do a = (a << 1) + 1 or a = (a << 1) | 1. Outside the while loop, we return the result a ^ N.

Solution

1
2
3
4
5
6
7
func bitwiseComplement(N int) int {
    a := 1
    for a < N {
        a = (a << 1) | 1
    }
    return a ^ N
}

Insert into a Binary Search Tree

You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.

Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.

Example 1:

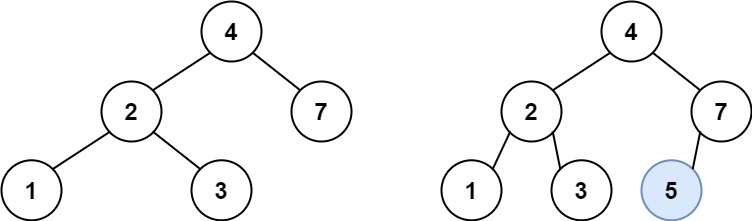
Insert into a Binary Search Tree

Insert into a Binary Search Tree

1
2
3
Input: root = [4,2,7,1,3], val = 5
Output: [4,2,7,1,3,5]
Explanation: Another accepted tree is:

Insert into a Binary Search Tree

Example 2:

1
2
Input: root = [40,20,60,10,30,50,70], val = 25
Output: [40,20,60,10,30,50,70,null,null,25]

Example 3:

1
2
Input: root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
Output: [4,2,7,1,3,5]

Constraints:

  • The number of nodes in the tree will be in the range [0, 104].

  • -10^8 <= Node.val <= 10^8

  • All the values Node.val are unique.

  • -10^8 <= val <= 10^8

  • It’s guaranteed that val does not exist in the original BST.

Explanation

  1. For tree problem, we can usually solve it using recursion. In this problem, we can solve it by recursively calling the main function.

  2. For example, using the problem’s example 1, 5 is greater than 4, so we check 4’s right child 7. Now 5 is less than 7, so we check 7’s left child which is NULL. Now we can just create a new TreeNode with value 5 and return it.

  3. The basecase is if root is NULL, we can just create a new TreeNode with value val and return it. Else if val is less than root, then we recursively call the main function with root.left and val, the return value will be root.left. Similarlly, if val is greater than root, then we recursively call the main function with root.right and val, the return value will be root.right. At the end, we return root.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func insertIntoBST(root *TreeNode, val int) *TreeNode {
    if root == nil { return &TreeNode{Val: val} }

    if val < root.Val {
        root.Left = insertIntoBST(root.Left, val)
    } else {
        root.Right = insertIntoBST(root.Right, val)
    }

    return root
}

Rotate List

Given a linked list, rotate the list to the right by k places, where k is non-negative.

Example 1:

1
2
3
4
5
Input: 1->2->3->4->5->NULL, k = 2
Output: 4->5->1->2->3->NULL
Explanation:
rotate 1 steps to the right: 5->1->2->3->4->NULL
rotate 2 steps to the right: 4->5->1->2->3->NULL

Example 2:

1
2
3
4
5
6
7
Input: 0->1->2->NULL, k = 4
Output: 2->0->1->NULL
Explanation:
rotate 1 steps to the right: 2->0->1->NULL
rotate 2 steps to the right: 1->2->0->NULL
rotate 3 steps to the right: 0->1->2->NULL
rotate 4 steps to the right: 2->0->1->NULL

Explanation

  1. We need two pointers, slow and fast. Fast pointer move k step ahead, then both slow and fast pointer move at the same time until fast pointer hits the end.

  2. Now, fast.next = head, head = slow.next, and slow.next = null.

  3. Corner case is when k is bigger than the size of the linkedlist. Actually, the k is k = k % size.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func rotateRight(head *ListNode, k int) *ListNode {
    if head == nil || head.Next == nil || k == 0 { return head }

    n := 1
    slow, fast := head, head

    for fast.Next != nil {
        n += 1
        fast = fast.Next
    }
    k = k % n
    if k == 0 { return head }

    fast = head
    for i := 0; i < k; i++ {
        fast = fast.Next
    }
    for fast.Next != nil {
        slow = slow.Next
        fast = fast.Next
    }

    fast.Next = head
    head = slow.Next
    slow.Next = nil

    return head
}

Week 2: October 8th - October 14th

Two Sum III - Data structure design

Design a data structure that accepts a stream of integers and checks if it has a pair of integers that sum up to a particular value.

Implement the TwoSum class:

  • TwoSum() Initializes the TwoSum object, with an empty array initially.

  • void add(int number) Adds number to the data structure.

  • boolean find(int value) Returns true if there exists any pair of numbers whose sum is equal to value, otherwise, it returns false.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input
["TwoSum", "add", "add", "add", "find", "find"]
[[], [1], [3], [5], [4], [7]]
Output
[null, null, null, null, true, false]

Explanation
TwoSum twoSum = new TwoSum();
twoSum.add(1);   // [] --> [1]
twoSum.add(3);   // [1] --> [1,3]
twoSum.add(5);   // [1,3] --> [1,3,5]
twoSum.find(4);  // 1 + 3 = 4, return true
twoSum.find(7);  // No two integers sum up to 7, return false

Constraints:

  • -10^5 <= number <= 10^5

  • -23^1 <= value <= 23^1 - 1

  • At most 5 * 10^4 calls will be made to add and find.

Explanation

  1. In the add method, We can use a HashMap to record the frequency of the added number. The key is the number, the value is the frequency.

  2. In the find method, we loop through the HashMap keyset’s every number num, the target will be value - num. Then we check if the hashmap contains the target, then we need to consider two cases. The first case is if the target is equal to the current number and the frequency of that number is 1, then we continue. The second case is if the target is not equal to the current number, that means we find a pair that sum to value so we return true. At the end when we loop through all the number, then we return false.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class TwoSum {
    Map<Integer, Integer> hm;

    /** Initialize your data structure here. */
    public TwoSum() {
        hm = new HashMap<>();
    }

    /** Add the number to an internal data structure.. */
    public void add(int number) {
        hm.put(number, hm.getOrDefault(number, 0) + 1);
    }

    /** Find if there exists any pair of numbers which sum is equal to the value. */
    public boolean find(int value) {
        for (int num: hm.keySet()) {
            int target = value - num;
            if (hm.containsKey(target)) {
                if (num == target && hm.get(num) == 1) {
                    continue;
                }
                return true;
            }
        }

        return false;
    }
}

/**
 * Your TwoSum object will be instantiated and called as such:
 * TwoSum obj = new TwoSum();
 * obj.add(number);
 * boolean param_2 = obj.find(value);
 */

Given a sorted (in ascending order) integer array nums of n elements and a target value, write a function to search target in nums. If target exists, then return its index, otherwise return -1.

Example 1:

1
2
3
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2:

1
2
3
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

Note:

  1. You may assume that all elements in nums are unique.

  2. n will be in the range [1, 10000].

  3. The value of each element in nums will be in the range [-9999, 9999].

Explanation

  1. Standard binary search. First, initialize the range left = 0, right = nums.length-1. While left <= right, we find the middle index mid = left + (right - left) / 2. Then compare target with nums[mid]. If nums[mid] == target, we return mid. Else if nums[mid] < target, then we update left = mid + 1. Else if nums[mid] < target, then we update right = mid - 1.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func search(nums []int, target int) int {
    left, right := 0, len(nums) - 1

    for left <= right {
        mid := left + (right - left) / 2
        if nums[mid] < target {
            left = mid + 1
        } else if nums[mid] > target {
            right = mid - 1
        } else {
            return mid
        }
    }

    return -1
}

Serialize and Deserialize BST

Serialization is converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary search tree. There is no restriction on how your serialization/deserialization algorithm should work. You need to ensure that a binary search tree can be serialized to a string, and this string can be deserialized to the original tree structure.

The encoded string should be as compact as possible.

Example 1:

1
2
Input: root = [2,1,3]
Output: [2,1,3]

Example 2:

1
2
Input: root = []
Output: []

Constraints:

  • The number of nodes in the tree is in the range [0, 10^4].

  • 0 <= Node.val <= 10^4

  • The input tree is guaranteed to be a binary search tree.

Explanation

  1. We can use level order traversal, in other word, BFS, to store all node value into a list, if the node is null, we can store any symbol, for example #. At the end, we can use String.join add , between the list element and return it as a string.

  2. In the deserialize method, first we split the string into array. Then if the first element is not #, we make a new TreeNode root with value equals to the first value of the array. Next, we store this root TreeNode into the queue. While the queue is not empty, we pop the queue to get popNode. If the popNode is not empty, we make a new node left = null and check if array[i] is not equals to #, then left have the value of array[i]. Next, connect popNode with left by popNode.left = left, and we store left into the queue and increase i. Same for right. Outside when queue is empty, we return the root.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

type Codec struct {

}

func Constructor() Codec {
    return Codec{}
}

// Serializes a tree to a single string.
func (this *Codec) serialize(root *TreeNode) string {
    lst := make([]string, 0)
    queue := make([]*TreeNode, 0)
    queue = append(queue, root)

    for len(queue) > 0 {
        popNode := queue[0]
        queue = queue[1:]
        if popNode != nil {
            lst = append(lst, strconv.Itoa(popNode.Val))
            queue = append(queue, popNode.Left)
            queue = append(queue, popNode.Right)
        } else {
            lst = append(lst, "#")
        }
    }

    return strings.Join(lst, ",")
}

// Deserializes your encoded data to tree.
func (this *Codec) deserialize(data string) *TreeNode {
    if data == "#" { return nil }
    arr := strings.Split(data, ",")
    queue := make([]*TreeNode, 0)
    rootVal, _ := strconv.Atoi(arr[0])
    root := &TreeNode{ Val: rootVal }

    queue = append(queue, root)
    i := 1

    for len(queue) > 0 {
        popNode := queue[0]
        queue = queue[1:]

        if popNode != nil {
            left := (*TreeNode)(nil)
            if arr[i] != "#" {
                leftVal, _ := strconv.Atoi(arr[i])
                left = &TreeNode{ Val: leftVal }
                popNode.Left = left
            } else {
                popNode.Left = nil
            }
            queue = append(queue, left)
            i += 1

            right := (*TreeNode)(nil)
            if arr[i] != "#" {
                rightVal, _ := strconv.Atoi(arr[i])
                right = &TreeNode{ Val: rightVal }
                popNode.Right = right
            } else {
                popNode.Right = nil
            }
            queue = append(queue, right)
            i += 1
        }
    }

    return root
}


/**
 * Your Codec object will be instantiated and called as such:
 * ser := Constructor()
 * deser := Constructor()
 * tree := ser.serialize(root)
 * ans := deser.deserialize(tree)
 * return ans
 */

Minimum Number of Arrows to Burst Balloons

There are some spherical balloons spread in two-dimensional space. For each balloon, provided input is the start and end coordinates of the horizontal diameter. Since it’s horizontal, y-coordinates don’t matter, and hence the x-coordinates of start and end of the diameter suffice. The start is always smaller than the end.

An arrow can be shot up exactly vertically from different points along the x-axis. A balloon with xstart and xend bursts by an arrow shot at x if xstart ≤ x ≤ xend. There is no limit to the number of arrows that can be shot. An arrow once shot keeps traveling up infinitely.

Given an array points where points[i] = [xstart, xend], return the minimum number of arrows that must be shot to burst all balloons.

Example 1:

1
2
3
Input: points = [[10,16],[2,8],[1,6],[7,12]]
Output: 2
Explanation: One way is to shoot one arrow for example at x = 6 (bursting the balloons [2,8] and [1,6]) and another arrow at x = 11 (bursting the other two balloons).

Example 2:

1
2
Input: points = [[1,2],[3,4],[5,6],[7,8]]
Output: 4

Example 3:

1
2
Input: points = [[1,2],[2,3],[3,4],[4,5]]
Output: 2

Example 4:

1
2
Input: points = [[1,2]]
Output: 1

Example 5:

1
2
Input: points = [[2,3],[2,3]]
Output: 1

Constraints:

  • 0 <= points.length <= 10^4

  • points[i].length == 2

  • -23^1 <= xstart < xend <= 23^1 - 1

Explanation

  1. First, we sort the horizontal lines by their starting points.

    1
    2
    3
    4
    5
    6
    7
    8
     -------
     ---------
          --------
                     ------
                        --------
                                    -------------------
                                       ----
                                               ------

  2. Next, we default the shooting point is the first ballon’s right ending point. If the second ballon’s starting point is less than or equals to the first boolean’s right ending point, then we update the shooting point be the minium of these two boolean’s right ending point. If the current boolean’s starting point is greater than the updated ending point, then we make another shoot, and the shooting point is the current boolean’s ending point.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func findMinArrowShots(points [][]int) int {
    if len(points) == 0 { return 0 }

    sort.Slice(points, func (i, j int) bool {
        return points[i][0] < points[j][0]
    })

    res := 1
    prevEnd := points[0][1]
    for i := 1; i < len(points); i++ {
        curStart, curEnd := points[i][0], points[i][1]
        if curStart <= prevEnd {
            prevEnd = min(prevEnd, curEnd)
        } else {
            res += 1
            prevEnd = curEnd
        }
    }

    return res
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Remove Duplicate Letters

Given a string s, remove duplicate letters so that every letter appears once and only once. You must make sure your result is the smallest in lexicographical order among all possible results.

Note: This question is the same as 1081: https://leetcode.com/problems/smallest-subsequence-of-distinct-characters/

Example 1:

1
2
Input: s = "bcabc"
Output: "abc"

Example 2:

1
2
Input: s = "cbacdcbc"
Output: "acdb"

Constraints:

  • 1 <= s.length <= 10^4

  • s consists of lowercase English letters.

Hint 1:

Greedily try to add one missing character. How to check if adding some character will not cause problems ? Use bit-masks to check whether you will be able to complete the sub-sequence if you add the character at some index i.

Explanation

  1. First, we create a HashMap to count the frequency of each character. Also, we create a visited map to keep track if the character is already appeared in the res string.

  2. Loop through every character in the string. Update its frequency, check if it’s already visited. If it’s visited, then we continue. If it’s not visited, then we compare it with the last character of the res string. While the current iterated element is smaller than the last character of the res string, and the last character from the res string still has frequency at least one, in other words, it will appear in the later iterated character. Then we delete that last character from the res string, and add the smaller iterated character to the string. Repeat this while loop until the current iterated character is greater than the last character of the res string, then we append the current iterated character to the res.

  3. Initially, we will add a '0' to the res string because it’s smaller than any letter, so that it is easier for us to do the comparison with the last character of the string. At the end, we will return res.substring(1) to ignore that first character.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func removeDuplicateLetters(s string) string {
    charFreq := make(map[byte]int32, 0)
    for i := range s {
        charFreq[s[i]] += 1
    }

    res := "0"

    visited := make(map[byte]bool)

    for i := range s {
        curChar := s[i]
        charFreq[curChar] -= 1

        if visited[curChar] == true { continue }

        for curChar < res[len(res)-1] && charFreq[res[len(res)-1]] > 0 {
            visited[res[len(res)-1]] = false
            res = res[:len(res)-1]
        }
        visited[curChar] = true
        res += string(curChar)
    }

    return res[1:]
}

Buddy Strings

Given two strings A and B of lowercase letters, return true if you can swap two letters in A so the result is equal to B, otherwise, return false.

Swapping letters is defined as taking two indices i and j (0-indexed) such that i != j and swapping the characters at A[i] and A[j]. For example, swapping at indices 0 and 2 in "abcd" results in "cbad".

Example 1:

1
2
3
Input: A = "ab", B = "ba"
Output: true
Explanation: You can swap A[0] = 'a' and A[1] = 'b' to get "ba", which is equal to B.

Example 2:

1
2
3
Input: A = "ab", B = "ab"
Output: false
Explanation: The only letters you can swap are A[0] = 'a' and A[1] = 'b', which results in "ba" != B.

Example 3:

1
2
3
Input: A = "aa", B = "aa"
Output: true
Explanation: You can swap A[0] = 'a' and A[1] = 'a' to get "aa", which is equal to B.

Example 4:

1
2
Input: A = "aaaaaaabc", B = "aaaaaaacb"
Output: true

Example 5:

1
2
Input: A = "", B = "aa"
Output: false

Constraints:

  • 0 <= A.length <= 20000

  • 0 <= B.length <= 20000

  • A and B consist of lowercase letters.

Explanation

  1. We can use brute force to solve this problem.

  2. First, if two strings have different length or string A’s length is less than 2, then return false immediately.

  3. If string A and string B are equal, but if string A’s all characters are unique, then we return false immediately because we can only swap two same characters in this case. We can use a HashSet to store all characters in string A, then check if the set’s size is less than string A’s length, that means there are same characters.

  4. If string A and string B are not equal, we can use a list to store the indexes when A[i] != B[i]. After looping checking all characters, if the list’s size is not equal to 2, we can return false immediately. If it’s equal to 2 that means there are two places the characters are different, we can compare these 4 characters and return the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func buddyStrings(A string, B string) bool {
    if len(A) != len(B) || len(A) < 2 { return false }

    set := make(map[byte]bool)
    for i := range A {
        set[A[i]] = true
    }

    if A == B {
        if len(set) < len(A) {
            return true
        } else {
            return false
        }
    }

    diffIdx := make([]int, 0)
    for i := 0; i < len(A); i++ {
        if A[i] != B[i] {
            diffIdx = append(diffIdx, i)
        }
        if len(diffIdx) > 2 { return false }
    }

    return len(diffIdx) == 2 && A[diffIdx[0]] == B[diffIdx[1]] && A[diffIdx[1]] == B[diffIdx[0]]
}

Sort List

Given the head of a linked list, return the list after sorting it in ascending order.

Follow up: Can you sort the linked list in O(n logn) time and O(1) memory (i.e. constant space)?

Example 1:

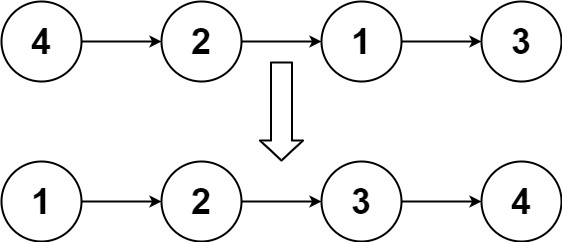
Sort List

1
2
Input: head = [4,2,1,3]
Output: [1,2,3,4]

Example 2:

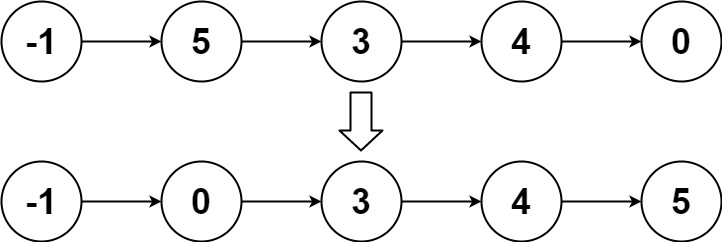
Sort List

1
2
Input: head = [-1,5,3,4,0]
Output: [-1,0,3,4,5]

Example 3:

1
2
Input: head = []
Output: []

Constraints:

  • The number of nodes in the list is in the range [0, 5 * 104].

  • -10^5 <= Node.val <= 10^5

Explanation

  1. We can use merge sort method to solve this problem.

  2. First we need to find the mid node or the right list’s head node. We can use slow and fast pointer technique to find the mid node.

  3. Next, we want to split the list into left list and right list. If the list is 1->2->3->4, we want the left list be 1->2 and the right list be 3->4. We can recursively call the main function with the left list, and recursively call the main function with the right list to spit the list.

  4. After splitting, we want to merge the left list and right list in a sorted order.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func sortList(head *ListNode) *ListNode {
    if head == nil || head.Next == nil { return head }

    mid := getMid(head)
    return merge(sortList(head), sortList(mid))
}

func getMid(head *ListNode) *ListNode {
    slow, fast := head, head.Next

    for fast != nil && fast.Next != nil {
        slow = slow.Next
        fast = fast.Next.Next
    }

    mid := slow.Next
    slow.Next = nil
    return mid
}

func merge(left, right *ListNode) *ListNode {
    if left == nil { return right }
    if right == nil { return left }

    dummy := &ListNode{Val: -1}
    tail := dummy

    for left != nil && right != nil {
        if left.Val < right.Val {
            tail.Next = left
            left = left.Next
        } else {
            tail.Next = right
            right = right.Next
        }
        tail = tail.Next
    }

    if left != nil {
        tail.Next = left
    }
    if right != nil {
        tail.Next = right
    }

    return dummy.Next
}

House Robber II

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have a security system connected, and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers nums representing the amount of money of each house, return the maximum amount of money you can rob tonight without alerting the police.

Example 1:

1
2
3
Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2), because they are adjacent houses.

Example 2:

1
2
3
4
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.

Example 3:

1
2
Input: nums = [0]
Output: 0

Constraints:

  • 1 <= nums.length <= 100

  • 0 <= nums[i] <= 1000

Hint 1:

Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money. Now the problem has degenerated to the House Robber, which is already been solved.

Explanation

  1. The problem’s hint basically answer the problem: Since House[1] and House[n] are adjacent, they cannot be robbed together. Therefore, the problem becomes to rob either House[1]-House[n-1] or House[2]-House[n], depending on which choice offers more money.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func rob(nums []int) int {
    if len(nums) == 1 { return nums[0] }
    if len(nums) == 2 { return max(nums[0], nums[1]) }

    return max(helper(nums, 0, len(nums)-2), helper(nums, 1, len(nums)-1))
}

func helper(nums []int, left, right int) int {
    if left == right { return nums[left] }
    n1, n2 := nums[left], max(nums[left], nums[left + 1])

    for i := left + 2; i <= right; i++ {
        n1, n2 = n2, max(nums[i] + n1, n2)
    }

    return n2
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Week 3: October 15th - October 21st

Meeting Rooms II

Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],...] (si < ei), find the minimum number of conference rooms required.

Example 1:

1
2
Input: [[0, 30],[5, 10],[15, 20]]
Output: 2

Example 2:

1
2
Input: [[7,10],[2,4]]
Output: 1

NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

Hint 1:

Think about how we would approach this problem in a very simplistic way. We will allocate rooms to meetings that occur earlier in the day v/s the ones that occur later on, right?

Hint 2:

If you’ve figured out that we have to sort the meetings by their start time, the next thing to think about is how do we do the allocation? There are two scenarios possible here for any meeting. Either there is no meeting room available and a new one has to be allocated, or a meeting room has freed up and this meeting can take place there.

Hint 3:

An important thing to note is that we don’t really care which room gets freed up while allocating a room for the current meeting. As long as a room is free, our job is done.

We already know the rooms we have allocated till now and we also know when are they due to get free because of the end times of the meetings going on in those rooms. We can simply check the room which is due to get vacated the earliest amongst all the allocated rooms.

Hint 4:

Following up on the previous hint, we can make use of a min-heap to store the end times of the meetings in various rooms.

So, every time we want to check if any room is free or not, simply check the topmost element of the min heap as that would be the room that would get free the earliest out of all the other rooms currently occupied.

If the room we extracted from the top of the min heap isn’t free, then no other room is. So, we can save time here and simply allocate a new room.

Explanation

  1. For interval problem, first we sort all intervals by their start time.

  2. If two interval overlap, that means the second interval’s start time is less than the first interval’s end time. If two interval don’t overlap, that means the second interval’s start time is equal or greater than the first interval’s end time.

  3. We can use a minHeap to record the end time we already interated. Initially, we append the first interval’s end time into the minHeap. Start looping from the second interval. If the current interval’s start time is less than the minHeap’s top end time, that means we have overlap so increase the result. Else the current interval’s start time is equal or greater than the minHeap’s top end time, so we can pop the minHeap until the current interval’s start time is less than the minHeap’s top end time; then we append the current interval’s end time.

  4. The minHeap’s size is the number of meeting we are now having, the res is the maximum number of overlapping meeting. So if minHeap.size() < res, we don’t need to increase res, we can just append the current interval’s end time to the minHeap. For example, in below’s graph, when the current interval is [4284, 5907], the minHeap only has [5870]. Even though 4284 < 5870, we just append the current interval’s end time to this minHeap.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
[[1293,2986],[848,3846],[4284,5907],[4466,4781],[518,2918],[300,5870]]

300                                                              5870
---------------------------------------------------------------------

    518                   2918
    --------------------------

        848                        3846
        -------------------------------

                 1293          2986
                 ------------------

                                             4284                            5907
                                             ------------------------------------

                                                      4466  4781
                                                      ----------

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int minMeetingRooms(int[][] intervals) {
        if (intervals.length == 0) return 0;

        Arrays.sort(intervals, (a, b) -> {
            return Integer.compare(a[0], b[0]);
        });
        Queue<Integer> minHeap = new PriorityQueue<>();

        int res = 1;
        minHeap.offer(intervals[0][1]);

        for (int i = 1; i < intervals.length; i++) {
            int curStart = intervals[i][0];
            int curEnd = intervals[i][1];
            if (minHeap.size() == res && curStart < minHeap.peek()) {
                res += 1;
            } else {
                while (!minHeap.isEmpty() && curStart >= minHeap.peek()) {
                    minHeap.poll();
                }
            }
            minHeap.offer(curEnd);
        }

        return res;
    }
}

Rotate Array

Given an array, rotate the array to the right by k steps, where k is non-negative.

Follow up:

  • Try to come up as many solutions as you can, there are at least 3 different ways to solve this problem.

  • Could you do it in-place with O(1) extra space?

Example 1:

1
2
3
4
5
6
Input: nums = [1,2,3,4,5,6,7], k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
rotate 1 steps to the right: [7,1,2,3,4,5,6]
rotate 2 steps to the right: [6,7,1,2,3,4,5]
rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

1
2
3
4
5
Input: nums = [-1,-100,3,99], k = 2
Output: [3,99,-1,-100]
Explanation:
rotate 1 steps to the right: [99,-1,-100,3]
rotate 2 steps to the right: [3,99,-1,-100]

Constraints:

  • 1 <= nums.length <= 2 * 10^4

  • -23^1 <= nums[i] <= 23^1 - 1

  • 0 <= k <= 10^5

Hint 1:

The easiest solution would use additional memory and that is perfectly fine.

Hint 2:

The actual trick comes when trying to solve this problem without using any additional memory. This means you need to use the original array somehow to move the elements around. Now, we can place each element in its original location and shift all the elements around it to adjust as that would be too costly and most likely will time out on larger input arrays.

Hint 3:

One line of thought is based on reversing the array (or parts of it) to obtain the desired result. Think about how reversal might potentially help us out by using an example.

Hint 4:

The other line of thought is a tad bit complicated but essentially it builds on the idea of placing each element in its original position while keeping track of the element originally in that position. Basically, at every step, we place an element in its rightful position and keep track of the element already there or the one being overwritten in an additional variable. We can’t do this in one linear pass and the idea here is based on cyclic-dependencies between elements.

Explanation

  1. We can use $O(1)$ space to solve this problem.

  2. First, reverse the whole array.

  3. Then, reverse the first k numbers.

  4. Finally, reverse the last len(nums)-k numbers.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func rotate(nums []int, k int)  {
    k = k % len(nums)
    reverse(nums, 0, len(nums) - 1)
    reverse(nums, 0, k - 1)
    reverse(nums, k, len(nums) - 1)
}

func reverse(nums []int, left, right int) {
    l, r := left, right
    for l < r {
        nums[l], nums[r] = nums[r], nums[l]
        l += 1
        r -= 1
    }
}

Search a 2D Matrix

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

  • Integers in each row are sorted from left to right.

  • The first integer of each row is greater than the last integer of the previous row.

Example 1:

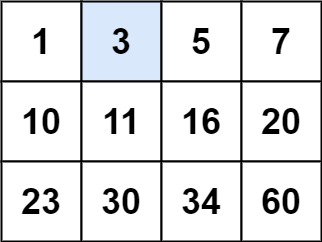
Search a 2D Matrix

1
2
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
Output: true

Example 2:

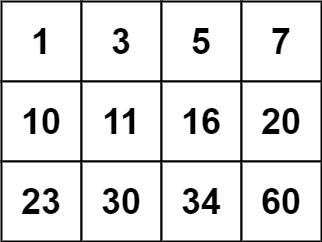
Search a 2D Matrix

1
2
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
Output: false

Example 3:

1
2
Input: matrix = [], target = 0
Output: false

Constraints:

  • m == matrix.length

  • n == matrix[i].length

  • 0 <= m, n <= 100

  • -10^4 <= matrix[i][j], target <= 10^4

Explanation

  1. We can think of all the subarrays are flatterned into one single array, then apply binary search to find the target element.

  2. If all elements are in a single array, then we have total row * col elements. So initially left = 0, right = row * col - 1. After we find the mid, it can transform back to a 2d array’s row as mid / col, column as mid % col.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func searchMatrix(matrix [][]int, target int) bool {
    if len(matrix) == 0 || len(matrix[0]) == 0 { return false }

    row, col := len(matrix), len(matrix[0])
    left, right := 0, row * col - 1

    for left <= right {
        mid := left + (right - left) / 2
        if matrix[mid / col][mid % col] < target {
            left = mid + 1
        } else if matrix[mid / col][mid % col] > target {
            right = mid - 1
        } else {
            return true;
        }
    }

    return false
}

Repeated DNA Sequences

All DNA is composed of a series of nucleotides abbreviated as 'A', 'C', 'G', and 'T', for example: "ACGAATTCCG". When studying DNA, it is sometimes useful to identify repeated sequences within the DNA.

Write a function to find all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule.

Example 1:

1
2
Input: s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
Output: ["AAAAACCCCC","CCCCCAAAAA"]

Example 2:

1
2
Input: s = "AAAAAAAAAAAAA"
Output: ["AAAAAAAAAA"]

Constraints:

  • 0 <= s.length <= 10^5

  • s[i] is 'A', 'C', 'G', or 'T'.

Explanation

  1. If the string has length less than or equal to 10, we return empty result.

  2. We can use brute force to solve this problem. First, we check the first 10 character string starts from index 0, then check the second 10 character string starts from index 1, etc. When iterating, we put them into a frequency map.

  3. At the end, all string that appears more than once in the frequency map are result string.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func findRepeatedDnaSequences(s string) []string {
    if len(s) <= 10 { return []string{} }

    strFreq := make(map[string]int)

    for start := 0; start + 9 < len(s); start++ {
        curStr := s[start:start+10]
        strFreq[curStr]++
    }

    res := make([]string, 0)
    for k, v := range strFreq {
        if v > 1 {
            res = append(res, k)
        }
    }

    return res
}

Best Time to Buy and Sell Stock IV

You are given an integer array prices where prices[i] is the price of a given stock on the ith day.

Design an algorithm to find the maximum profit. You may complete at most k transactions.

Notice that you may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

Example 1:

1
2
3
Input: k = 2, prices = [2,4,1]
Output: 2
Explanation: Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.

Example 2:

1
2
3
Input: k = 2, prices = [3,2,6,5,0,3]
Output: 7
Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.

Constraints:

  • 0 <= k <= 10^9

  • 0 <= prices.length <= 10^4

  • 0 <= prices[i] <= 1000

Explanation

  1. We can use dynamic programming to solve this problem.

  2. Dynamic state is a two dimensional array dp[t][d], row is transaction and column is the day, and it represents the maximum profit can be made using at most t transaction in d day. Note, the length of the row is t+1 because we need consider zero transaction.

  3. Dynamic init is dp[0][d] (top row) all values will be zero because we are not making any transaction. dp[t][0] all (left column) will be zero because if only has one day, then we can’t make any profit for one day.

  4. Dynamic function will be taking the maximum profit of either not making any transaction on day d, which is dp[t][d-1]; another way is make transaction on day d, which the profit will be prices[d] - prices[m] + dp[t-1][m], where m will be the day we buy the stock and sell this stock on day d for the last transaction and m will be from 0 to d-1. How do we find the m? We can switch the order of prices[d] - prices[m] + dp[t-1][m] to prices[d] + (dp[t-1][m] - prices[m]), so we need to find the m that makse the maximum of dp[t-1][m] - prices[m], let’s call this maxDiff. So, we can iterate the m from 0 to d-1, and find the maximum of maxDiff. Therefore, the dynamic function is max(dp[t][d-1], prices[d] + maxDiff where maxDiff = dp[t-1][m]-prices[m] for m = 0 to d-1.

  5. Dynamic result will be the bottom right value, which is dp[t][d].

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
func maxProfit(k int, prices []int) int {
    if len(prices) == 0 { return 0 }

    if k * 2 >= len(prices) {
        profit := 0
        for i := 1; i < len(prices); i++ {
            profit += max(prices[i] - prices[i-1], 0)
        }
        return profit
    }

    prev := make([]int, len(prices))
    res := make([]int, len(prices))

    for t := 1; t <= k; t++ {
        maxDiff := -prices[0]
        for d := 1; d < len(prices); d++ {
            res[d] = max(res[d-1], prices[d] + maxDiff)
            maxDiff = max(maxDiff, prev[d] - prices[d])
        }

        copy(prev, res)
    }

    return res[len(res) - 1]
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Minimum Domino Rotations For Equal Row

In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the ith domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the ith domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

Example 1:

Minimum Domino Rotations For Equal Row

1
2
3
4
5
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation:
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

1
2
3
4
Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation:
In this case, it is not possible to rotate the dominoes to make one row of values equal.

Constraints:

  • 2 <= A.length == B.length <= 2 * 10^4

  • 1 <= A[i], B[i] <= 6

Explanation

  1. We want either one row to have the same number target, there are can be only two choices, either all row to be A[0] or B[0].

  2. First, we create a helper function and assume the target is A[0]. Loop len(A) times, in each iteration, we check if both A[i] and B[i] are not equal to A[0], that means we cannot use A[0] as the target, so we return -1 from the helper function. Else if A[i] is not equal to target, then we increase cntA which means flip row A. Similarlly, else if B[i] is not equal to target, then we increase cntB which means flip row B. At the end we return the minimum between cntA and cntB.

  3. If the result res return from the helper function with target equals to A[0] is -1, then we run the helper function with target B[0] and return that value, else if the res return from the helper function with target equals to A[0] is not -1, then we return res; in this case, why don’t we need to try target is B[0]? Because if we try target is B[0], its answer will either be -1 or equal to res when target is A[0]. For example, if A = [5, 5, 5, 1], and B = [1, 1, 1, 5]. When target is either 5 or 1, the result is the same.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func minDominoRotations(A []int, B []int) int {
    res := helper(A, B)

    if res != -1 {
        return res
    } else {
        return helper(B, A)
    }
}

func helper(A, B []int) int {
    target := A[0]
    cntA, cntB := 0, 0

    for i := 0; i < len(A); i++ {
        if A[i] != target && B[i] != target {
            return -1
        } else if A[i] != target {
            cntA += 1
        } else if B[i] != target {
            cntB += 1
        }
    }

    if cntA < cntB {
        return cntA
    } else {
        return cntB
    }
}

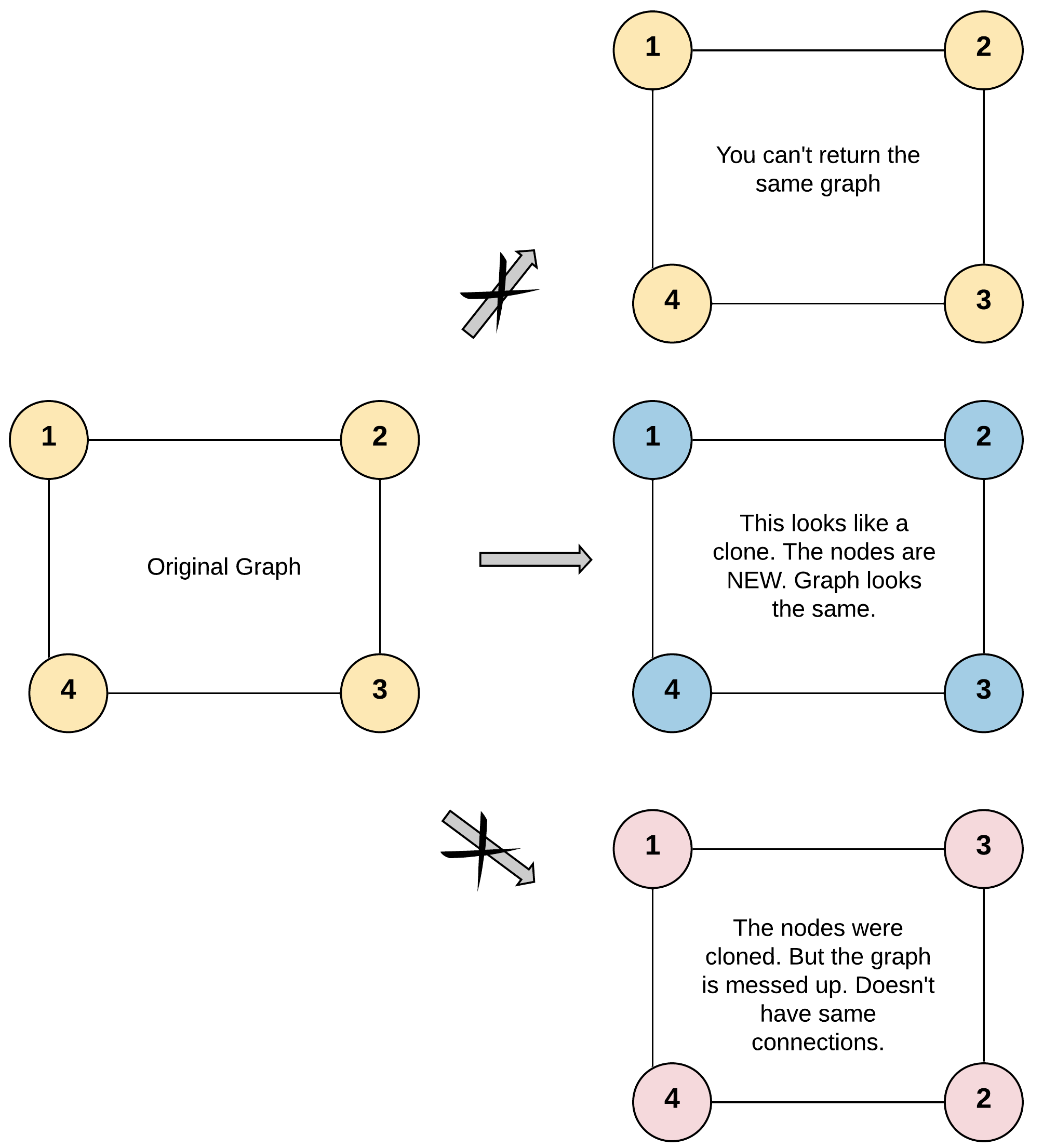
Clone Graph

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

1
2
3
4
class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

Clone Graph

1
2
3
4
5
6
7
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

Clone Graph

1
2
3
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

1
2
3
Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

Clone Graph

1
2
Input: adjList = [[2],[1]]
Output: [[2],[1]]

Constraints:

  • 1 <= Node.val <= 100

  • Node.val is unique for each node.

  • Number of Nodes will not exceed 100.

  • There is no repeated edges and no self-loops in the graph.

  • The Graph is connected and all nodes can be visited starting from the given node.

Explanation

  1. We can use DFS and a HashMap to solve this problem.

  2. In DFS, we iterate every node. In each iteration, we create a copy of the node and put its value as key, the copied node as value into the hashmap. Then loop through the original node’s neighbors and recursively call each neighbor with DFS. But before we recursively call the function, we check if the neighbor is in the hashmap or not. If not, then we call; and the return value will be added to the current copied node’s neighbor list. Else if the neighbor node’s value is already in the hashmap, then we don’t need to recursively call the DFS function, we can simply add the mapping node to the current copied node’s neighbor list.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a Node.
 * type Node struct {
 *     Val int
 *     Neighbors []*Node
 * }
 */

func cloneGraph(node *Node) *Node {
    if node == nil { return node }
    hm := make(map[int]*Node)
    return helper(node, hm)
}

func helper(node *Node, hm map[int]*Node) *Node {
    myNode := &Node{node.Val, make([]*Node, 0)}
    hm[node.Val] = myNode

    for _, neighbor := range node.Neighbors {
        if _, ok := hm[neighbor.Val]; !ok {
            myNeighbor := helper(neighbor, hm)
            myNode.Neighbors = append(myNode.Neighbors, myNeighbor)
        } else {
            myNode.Neighbors = append(myNode.Neighbors, hm[neighbor.Val])
        }
    }

    return myNode
}

Asteroid Collision

We are given an array asteroids of integers representing asteroids in a row.

For each asteroid, the absolute value represents its size, and the sign represents its direction (positive meaning right, negative meaning left). Each asteroid moves at the same speed.

Find out the state of the asteroids after all collisions. If two asteroids meet, the smaller one will explode. If both are the same size, both will explode. Two asteroids moving in the same direction will never meet.

Example 1:

1
2
3
Input: asteroids = [5,10,-5]
Output: [5,10]
Explanation: The 10 and -5 collide resulting in 10.  The 5 and 10 never collide.

Example 2:

1
2
3
Input: asteroids = [8,-8]
Output: []
Explanation: The 8 and -8 collide exploding each other.

Example 3:

1
2
3
Input: asteroids = [10,2,-5]
Output: [10]
Explanation: The 2 and -5 collide resulting in -5. The 10 and -5 collide resulting in 10.

Example 4:

1
2
3
Input: asteroids = [-2,-1,1,2]
Output: [-2,-1,1,2]
Explanation: The -2 and -1 are moving left, while the 1 and 2 are moving right. Asteroids moving the same direction never meet, so no asteroids will meet each other.

Constraints:

  • 1 <= asteroids <= 10^4

  • -1000 <= asteroids[i] <= 1000

  • asteroids[i] != 0

Hint 1:

Say a row of asteroids is stable. What happens when a new asteroid is added on the right?

Explanation

  1. This is a stack problem.

  2. Loop through the input array, put each iterated number into the stack. While the top of stack topNum is positive and the current iterated number is negative, then there’s a collision. While there’s collision, we compare if abs(topNum) < curNum, then we pop from stack and continue this while check. Else if abs(topNum) == curNum, we pop from stack, break from this while loop and don’t push the current number, so mark pushNum = false. Else if abs(topNum) > curNum, we break from this while loop and don’t push current number. After the while loop and pushNum is still true, then we push the current number.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func asteroidCollision(asteroids []int) []int {
    st := make([]int, 0)

    for _, num := range asteroids {
        pushNum := true

        for len(st) > 0 && st[len(st)-1] > 0 && num < 0 {
            topNum := st[len(st)-1]

            if topNum < -num {
                st = st[:len(st)-1]
            } else if topNum == -num {
                st = st[:len(st)-1]
                pushNum = false
                break
            } else {
                pushNum = false
                break
            }
        }

        if pushNum == true {
            st = append(st, num)
        }
    }

    return st;
}

Week 4: October 22nd - October 28th

Search in a Sorted Array of Unknown Size

Given an integer array sorted in ascending order, write a function to search target in nums. If target exists, then return its index, otherwise return -1. However, the array size is unknown to you. You may only access the array using an ArrayReader interface, where ArrayReader.get(k) returns the element of the array at index k (0-indexed).

You may assume all integers in the array are less than 10000, and if you access the array out of bounds, ArrayReader.get will return 2147483647.

Example 1:

1
2
3
Input: array = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2:

1
2
3
Input: array = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

Constraints:

  • You may assume that all elements in the array are unique.

  • The value of each element in the array will be in the range [-9999, 9999].

  • The length of the array will be in the range [1, 10^4].

Explanation

  1. My first attempt is to use binary search to find the array’s length, then use binary search again to find the target.

  2. Actually we can assume the array’s length is INT_MAX and assume elements that are outside the array have values INT_MAX. Since this array is sorted and every array element is less than INT_MAX, we can use binary search to find out the target element.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * // This is ArrayReader's API interface.
 * // You should not implement it, or speculate about its implementation
 * interface ArrayReader {
 *     public int get(int index) {}
 * }
 */

class Solution {
    public int search(ArrayReader reader, int target) {
        int left = 0, right = 100000;

        while (left < right) {
            int mid = left + (right - left) / 2;
            int val = reader.get(mid);
            if (val < target) {
                left = mid + 1;
            } else if (val > target) {
                right = mid;
            } else {
                return mid;
            }
        }

        return -1;
    }
}

Minimum Depth of Binary Tree

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

Minimum Depth of Binary Tree

1
2
Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

1
2
Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Constraints:

  • The number of nodes in the tree is in the range [0, 10^5].

  • -1000 <= Node.val <= 1000

Explanation

  1. We can use level-order traversal to solve this problem. In the current level, if the node poll from the queue which is a leaf node, then we return the result or the number of level immediately, else if the poll node is not a leaf node, then we append its left child node and right child node to the queue.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minDepth(root *TreeNode) int {
    if root == nil { return 0 }
    res := 1
    queue := make([]*TreeNode, 0)
    queue = append(queue, root)

    for len(queue) > 0 {
        for i := len(queue) - 1; i >= 0; i-- {
            pollNode := queue[0]
            queue = queue[1:]
            if pollNode.Left == nil && pollNode.Right == nil {
                return res
            }
            if pollNode.Left != nil { queue = append(queue, pollNode.Left) }
            if pollNode.Right != nil { queue = append(queue, pollNode.Right) }
        }
        res += 1
    }

    return res
}

132 Pattern

Given an array of n integers nums, a 132 pattern is a subsequence of three integers nums[i], nums[j] and nums[k] such that i < j < k and nums[i] < nums[k] < nums[j].

Return true if there is a 132 pattern in nums, otherwise, return false.

Follow up: The O(n^2) is trivial, could you come up with the O(n logn) or the O(n) solution?

Example 1:

1
2
3
Input: nums = [1,2,3,4]
Output: false
Explanation: There is no 132 pattern in the sequence.

Example 2:

1
2
3
Input: nums = [3,1,4,2]
Output: true
Explanation: There is a 132 pattern in the sequence: [1, 4, 2].

Example 3:

1
2
3
Input: nums = [-1,3,2,0]
Output: true
Explanation: There are three 132 patterns in the sequence: [-1, 3, 2], [-1, 3, 0] and [-1, 2, 0].

Constraints:

  • n == nums.length

  • 1 <= n <= 10^4

  • -10^9 <= nums[i] <= 10^9

Explanation

  1. We can use monotonous stack to solve this problem in $O(n)$ runtime.

  2. If the input array is [2, 4, 2, 3, 5]. We loop from the right to left, and make a stack [2, 3, 5] (2 is the top of stack, the upper the stack, the lower the number). In the iteration we iterate to 4, we check 4 is greater than 2, we pop 2, update the pattern’s third number third=2; now 4 is greater than 3, we pop 3, update third=3; now 4 is less than 5, we push 4 into the stack, so we have [4, 5] (4 is the top of stack). Next iteration, we iterate the 2, since 2 < third, we return true because now we find a 132 pattern which is 2, 4, 3.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func find132pattern(nums []int) bool {
    if len(nums) < 3 { return false }

    st := make([]int, 0)
    third := math.MinInt32

    for i := len(nums)-1; i >= 0; i-- {
        if nums[i] < third { return true }

        for len(st) > 0 && nums[i] > st[len(st)-1] {
            third = st[len(st)-1]
            st = st[:len(st)-1]
        }
        st = append(st, nums[i])
    }

    return false
}

Bag of Tokens

You have an initial power of P, an initial score of 0, and a bag of tokens where tokens[i] is the value of the ith token (0-indexed).

Your goal is to maximize your total score by potentially playing each token in one of two ways:

If your current power is at least tokens[i], you may play the ith token face up, losing tokens[i] power and gaining 1 score.

If your current score is at least 1, you may play the ith token face down, gaining tokens[i] power and losing 1 score.

Each token may be played at most once and in any order. You do not have to play all the tokens.

Return the largest possible score you can achieve after playing any number of tokens.

Example 1:

1
2
3
Input: tokens = [100], P = 50
Output: 0
Explanation: Playing the only token in the bag is impossible because you either have too little power or too little score.

Example 2:

1
2
3
4
Input: tokens = [100,200], P = 150
Output: 1
Explanation: Play the 0th token (100) face up, your power becomes 50 and score becomes 1.
There is no need to play the 1st token since you cannot play it face up to add to your score.

Example 3:

1
2
3
4
5
6
7
Input: tokens = [100,200,300,400], P = 200
Output: 2
Explanation: Play the tokens in this order to get a score of 2:
1. Play the 0th token (100) face up, your power becomes 100 and score becomes 1.
2. Play the 3rd token (400) face down, your power becomes 500 and score becomes 0.
3. Play the 1st token (200) face up, your power becomes 300 and score becomes 1.
4. Play the 2nd token (300) face up, your power becomes 0 and score becomes 2.

Constraints:

  • 0 <= tokens.length <= 1000

  • 0 <= tokens[i], P < 10^4

Explanation

  1. We can use greedy approach to solve this problem.

  2. We want to spend less power and gain more score; and if not enough power, then we want to spend 1 score and gain more power.

  3. First, sort the array. Create a pointer i points to the smallest token, and a pointer j points to the largest token. If we have enough power (P >= tokens[i]) to gain score, then we spend our power and increase our score. At the same time, we keep track of the maximum score. Then move i to the right. Else if we don’t have enough power to gain score, then we want to spend 1 score and gain the most power. So we subtract 1 from our score, increase our power, and move j to the left.

  4. When pointer i > j, we break out the loop and return the maximum score we keep tracked.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func bagOfTokensScore(tokens []int, P int) int {
    res := 0
    sort.Ints(tokens)
    S := 0
    i, j := 0, len(tokens) - 1

    for i <= j {
        if P >= tokens[i] {
            S += 1
            res = max(res, S)
            P -= tokens[i]
            i += 1
        } else {
            if S == 0 { break }
            P += tokens[j]
            S -= 1
            j -= 1
        }
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Stone Game IV

Alice and Bob take turns playing a game, with Alice starting first.

Initially, there are n stones in a pile. On each player’s turn, that player makes a move consisting of removing any non-zero square number of stones in the pile.

Also, if a player cannot make a move, he/she loses the game.

Given a positive integer n. Return True if and only if Alice wins the game otherwise return False, assuming both players play optimally.

Example 1:

1
2
3
Input: n = 1
Output: true
Explanation: Alice can remove 1 stone winning the game because Bob doesn't have any moves.

Example 2:

1
2
3
Input: n = 2
Output: false
Explanation: Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).

Example 3:

1
2
3
Input: n = 4
Output: true
Explanation: n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).

Example 4:

1
2
3
4
5
Input: n = 7
Output: false
Explanation: Alice can't win the game if Bob plays optimally.
If Alice starts removing 4 stones, Bob will remove 1 stone then Alice should remove only 1 stone and finally Bob removes the last one (7 -> 3 -> 2 -> 1 -> 0).
If Alice starts removing 1 stone, Bob will remove 4 stones then Alice only can remove 1 stone and finally Bob removes the last one (7 -> 6 -> 2 -> 1 -> 0).

Example 5:

1
2
3
Input: n = 17
Output: false
Explanation: Alice can't win the game if Bob plays optimally.

Constraints:

  • 1 <= n <= 10^5

Hint 1:

Use dynamic programming to keep track of winning and losing states. Given some number of stones, Alice can win if she can force Bob onto a losing state.

Explanation 1

  1. We can use recursive/dynamic programming (top down) to solve this problem.

  2. Base case is if n is 0, then we return false immediately.

  3. We define a helper function, for example helper(5) represents if Alice can win when n is 5. In this case, we can try remove 1 stone, then recursively call the helper function helper(4). If helper(4) returns false, that means Bob lose the game, so Alice win. In other word, if helper(4) == false, then helper(5) = win. Else if helper(4) is true, then we keep try removing 2 * 2 = 4 stones. Now, Bob left with (5 - 4 = 1) stone, we check if helper(1) is false, then Alice can win. But helper(1) is true, so we keep try removing 3 * 3 = 9 stones, since there are total 5 stones, we cannot remove 9 stones. So after we try all possibilities and cannot find any recursive function returns false, then Alice lose the game.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func winnerSquareGame(n int) bool {
    hm := make(map[int]bool)
    return helper(n, hm)
}

func helper(n int, hm map[int]bool) bool {
    if _, ok := hm[n]; ok {
        return hm[n]
    }
    if n == 0 { return false }

    for i := 1; i * i <= n; i++ {
        nextRes := helper(n - i * i, hm)
        if nextRes == false {
            hm[n] = true
            return true
        }
    }

    hm[n] = false
    return false
}

Explanation 2

  1. We can also use bottom up approach to solve this problem.

  2. First, we create a boolean array dp that has size n + 1, and dp[i] represents if number i can win or not.

  3. Loop from i = 1 to i = n inclusive. For each i, inner loop j from 1 to j * j <= n, and j represents the number of stones we try to remove. If dp[i - j * j] is false, that means dp[i] is true.

  4. At the end, we return dp[n].

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func winnerSquareGame(n int) bool {
    hm := make(map[int]bool)
    return helper(n, hm)
}

func helper(n int, hm map[int]bool) bool {
    dp := make([]bool, n + 1)
    dp[0] = false;

    for i := 1; i <= n; i++ {
        for j := 1; j * j <= i; j++ {
            if dp[i - j * j] == false {
                dp[i] = true
                break
            }
        }
    }

    return dp[n]
}

Champagne Tower

We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row. Each glass holds one cup of champagne.

Then, some champagne is poured into the first glass at the top. When the topmost glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has its excess champagne fall on the floor.)

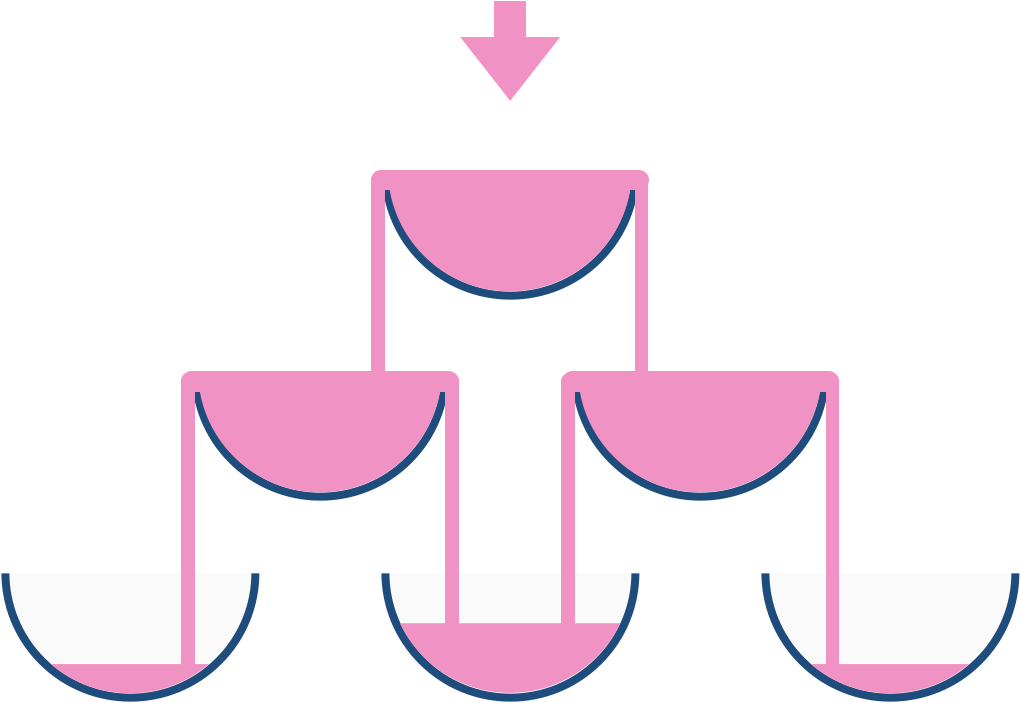
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full - there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.

Champagne Tower

Now after pouring some non-negative integer cups of champagne, return how full the jth glass in the ith row is (both i and j are 0-indexed.)

Example 1:

1
2
3
Input: poured = 1, query_row = 1, query_glass = 1
Output: 0.00000
Explanation: We poured 1 cup of champange to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.

Example 2:

1
2
3
Input: poured = 2, query_row = 1, query_glass = 1
Output: 0.50000
Explanation: We poured 2 cups of champange to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.

Example 3:

1
2
Input: poured = 100000009, query_row = 33, query_glass = 17
Output: 1.00000

Constraints:

  • 0 <= poured <= 10^9

  • 0 <= query_glass <= query_row < 100

Explanation 1

  1. If there are 3 cups of champagne are poured on the topmost glass, then the topmost glass is full, (3 - 1) = 2 cups of champagne will be poured equally on the next row’s left glass and right glass, so the second row’s first glass get 2 / 2 = 1 cup, and the right glass get 2 / 2 = 1 cup.

  2. If there are 4 cups of champagne are poured on the topmost glass, then the topmost glass is full, (4 - 1) = 3 cups of champagne will be poured equally on the next row’s left glass and right glass, so the second row’s first glass get 3 / 2 = 1.5 cup, and the right glass get 3 / 2 = 1.5 cup. Now, we iterate to second row. Since the second row’s first glass has 1.5 cup, it will poured equally on the next row’s left glass and right glass. So the second row’s first cup is full and (1.5 - 1 = 0.5) cup will be poured equally on the third row’s first glass and second glass. Similarlly, since the second row’s second glass has 1.5 cup, it will become full, and (1.5 - 1 = 0.5) cup will be poured equally on the third row’s second glass and third glass equally.

  3. We can use dynamic programming to solve this problem.

  4. Dynamic state is dp[r][c] represents the r row and c column’s glass of champagne.

  5. Dynamic init is dp[0][0] equals to the input poured.

  6. Dynamic function is if the current glass is full, it will split equally to the next row’s left glass and right glass. In other words, dp[r+1][c] = (dp[r][c] - 1) / 2.0 and dp[r+1][c+1] = (dp[r][c] - 1) / 2.0.

  7. Dynamic result is dp[query_row][query_glass].

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func champagneTower(poured int, query_row int, query_glass int) float64 {
    dp := make([][]float64, 100)
    for i := range dp {
        dp[i] = make([]float64, 100)
    }
    dp[0][0] = float64(poured)

    for r := 0; r < query_row; r++ {
        for c := 0; c <= r; c++ {
            if dp[r][c] > 1 {
                dp[r + 1][c] += (dp[r][c] - 1) / 2.0
                dp[r + 1][c + 1] += (dp[r][c] - 1) / 2.0
            }
        }
    }

    return min(1.0, dp[query_row][query_glass])
}

func min(a, b float64) float64 {
    if a < b {
        return a
    } else {
        return b
    }
}

Explanation 2

  1. Since the current row’s glass is depends on the last row’s glass only, we can also use one dymensional array to solve this problem.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func champagneTower(poured int, query_row int, query_glass int) float64 {
    dp := make([]float64, 100)
    dp[0] = float64(poured)

    for r := 0; r < query_row; r++ {
        for c := r; c >= 0; c-- {
            if dp[c] > 1 {
                dp[c + 1] += (dp[c] - 1) / 2.0
                dp[c] = (dp[c] - 1) / 2.0
            } else {
                dp[c] = 0
            }
        }
    }

    return min(1.0, dp[query_glass])
}

func min(a, b float64) float64 {
    if a < b {
        return a
    } else {
        return b
    }
}

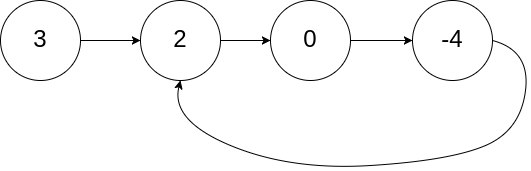
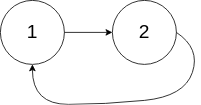
Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Notice that you should not modify the linked list.

Follow up:

Can you solve it using O(1) (i.e. constant) memory?

Example 1:

Linked List Cycle II

1
2
3
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Linked List Cycle II

1
2
3
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Linked List Cycle II

1
2
3
Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

  • The number of the nodes in the list is in the range [0, 10^4].

  • -10^5 <= Node.val <= 10^5

  • pos is -1 or a valid index in the linked-list.

Explanation

  1. Both slow and fast pointers point to the head.

  2. While fast and fast.next is not null, when slow pointer moves one step, fast pointer moves two steps.

  3. If slow pointer and fast pointer points to the same node, then it means there’s cycle, break out of the while loop.

  4. When out of the while loop, we first check if the fast pointer hits the end, if either fast or fast.next is null, then it means no cycle.

  5. Now, slow pointer moves back to the head. Fast pointer doesn’t move.

  6. Then run both, slow pointer and fast pointer at the same speed, the point the meet is the entry of cycle.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
func detectCycle(head *ListNode) *ListNode {
    if head == nil || head.Next == nil { return nil }

    slow, fast := head, head

    for fast != nil && fast.Next != nil {
        slow = slow.Next
        fast = fast.Next.Next
        if slow == fast { break }
    }

    if slow != fast { return nil }

    slow = head

    for slow != fast {
        slow = slow.Next
        fast = fast.Next
    }

    return slow
}

Summary Ranges

You are given a sorted unique integer array nums.

Return the smallest sorted list of ranges that cover all the numbers in the array exactly. That is, each element of nums is covered by exactly one of the ranges, and there is no integer x such that x is in one of the ranges but not in nums.

Each range [a,b] in the list should be output as:

  • "a->b" if a != b

  • "a" if a == b

Example 1:

1
2
3
4
5
6
Input: nums = [0,1,2,4,5,7]
Output: ["0->2","4->5","7"]
Explanation: The ranges are:
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"

Example 2:

1
2
3
4
5
6
7
Input: nums = [0,2,3,4,6,8,9]
Output: ["0","2->4","6","8->9"]
Explanation: The ranges are:
[0,0] --> "0"
[2,4] --> "2->4"
[6,6] --> "6"
[8,9] --> "8->9"

Example 3:

1
2
Input: nums = []
Output: []

Example 4:

1
2
Input: nums = [-1]
Output: ["-1"]

Example 5:

1
2
Input: nums = [0]
Output: ["0"]

Constraints:

  • 0 <= nums.length <= 20

  • -2^31 <= nums[i] <= 2^31 - 1

  • All the values of nums are unique.

Explanation

  1. Loop through the string, mark the current number as left. While the current number nums[i] plus one equal to the next number nums[i+1], increase i. Until the current number is not equal to the next number. Now, nums[i] is the right. If left and right are not the same, we find the push the left range and right range to the result list. If they left and right are the same, that means only one number of the range, and we push either left or right to the list.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func summaryRanges(nums []int) []string {
    res := make([]string, 0)
    if len(nums) == 0 { return res }

    for i := 0; i < len(nums); i++ {
        left := nums[i]
        for i + 1 < len(nums) && nums[i] + 1 == nums[i+1] {
            i += 1
        }
        right := nums[i]

        if left == right {
            res = append(res, strconv.Itoa(left))
        } else {
            res = append(res, strconv.Itoa(left) + "->" + strconv.Itoa(right))
        }
    }

    return res
}

Week 5: October 29th - October 31st

Encode N-ary Tree to Binary Tree

Design an algorithm to encode an N-ary tree into a binary tree and decode the binary tree to get the original N-ary tree. An N-ary tree is a rooted tree in which each node has no more than N children. Similarly, a binary tree is a rooted tree in which each node has no more than 2 children. There is no restriction on how your encode/decode algorithm should work. You just need to ensure that an N-ary tree can be encoded to a binary tree and this binary tree can be decoded to the original N-nary tree structure.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See following example).

For example, you may encode the following 3-ary tree to a binary tree in this way:

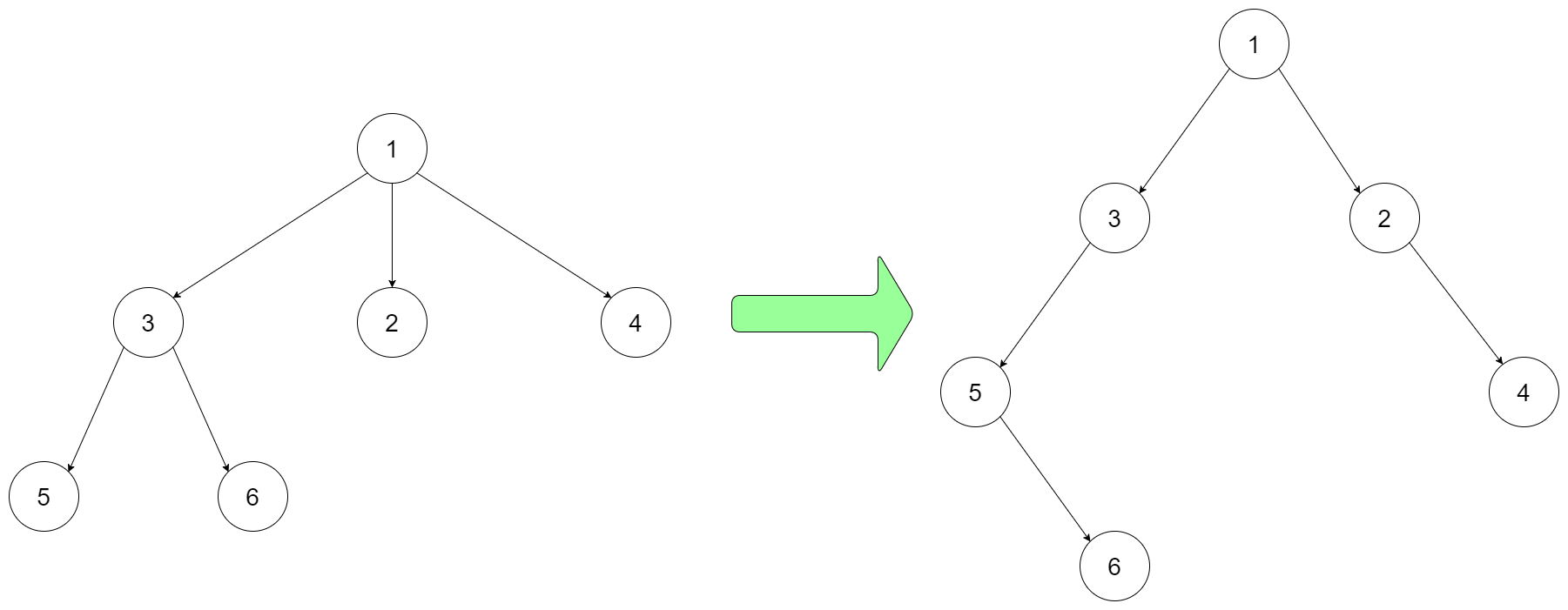
Encode N-ary Tree to Binary Tree

1
Input: root = [1,null,3,2,4,null,5,6]

Note that the above is just an example which might or might not work. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Constraints:

  • The height of the n-ary tree is less than or equal to 1000

  • The total number of nodes is between [0, 10^4]

  • Do not use class member/global/static variables to store states. Your encode and decode algorithms should be stateless.

Explanation

  1. One way to encode the N-ary tree to a binary tree is using the method on Wikipedia. For example:

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
     N-ary Tree:

       1
    /  |  \
   3   2   4
  / \
 5   6


 Binary Tree:

     1
    /
   3
  / \
 5   2
  \   \
   6   4

  2. In the above example, 3, 2, 4 are in the same level under the parent node 1. First, we put this level’s first child node 3 as the parent node’s left child. Then all other child nodes 2, 4 will be put under the first child node 3’s right side. Similarlly, for the parent node 3, it has children 5, 6. We put this level’s first child node 5 as node 3’s left child node. Then all other child nodes 6 will be put under the first child node 5’s right side.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Codec {
    // Encodes an n-ary tree to a binary tree.
    public TreeNode encode(Node root) {
        if (root == null) return null;
        TreeNode res = new TreeNode(root.val);
        if (!root.children.isEmpty()) {
            res.left = encode(root.children.get(0));
        }
        TreeNode cur = res.left;
        for (int i = 1; i < root.children.size(); i++) {
            cur.right = encode(root.children.get(i));
            cur = cur.right;
        }
        return res;
    }

    // Decodes your binary tree to an n-ary tree.
    public Node decode(TreeNode root) {
        if (root == null) return null;
        Node res = new Node(root.val, new ArrayList<>());
        TreeNode cur = root.left;
        while (cur != null) {
            res.children.add(decode(cur));
            cur = cur.right;
        }
        return res;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.decode(codec.encode(root));

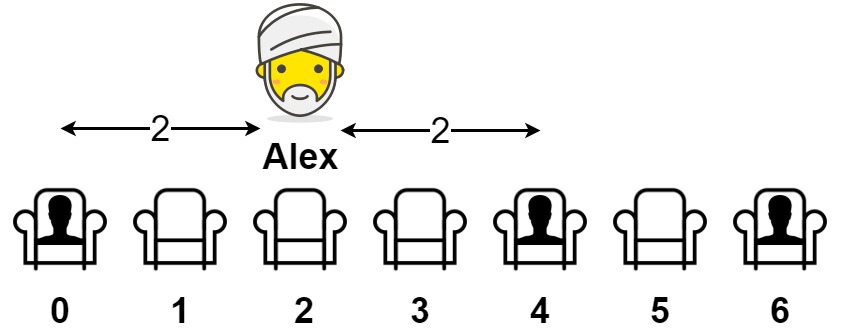
Maximize Distance to Closest Person

You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.

Return that maximum distance to the closest person.

Example 1:

Maximize Distance to Closest Person

1
2
3
4
5
6
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation:
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2:

1
2
3
4
5
Input: seats = [1,0,0,0]
Output: 3
Explanation:
If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Example 3:

1
2
Input: seats = [0,1]
Output: 1

Constraints:

  • 2 <= seats.length <= 2 * 10^4

  • seats[i] is 0 or 1.

  • At least one seat is empty.

  • At least one seat is occupied.

Explanation

  1. We need to consider 3 cases. First case is there are left neighbor and right neighbor. For example, if the input is [1, 0, 0, 0, 1], then Alex should sit in the middle, and the result is (rightNeighborIdx - leftNeighborIdx) / 2 = (4 - 0) / 2 = 2.

  2. Second case is there is no left neighbor. For example, if the input is [0, 0, 1], then Alex should sit in the first seat, and the result is equal to the first neighbor’s index which is 2.

  3. Third case is there is no right neighbor. For example, if the input is [1, 0, 0], then Alex should sit in the last seat, and the result is equal to lastIdx - lastNeighborIdx = 2 - 0 = 2.

  4. Initially, we need to find the first neighbor index, and initialize the result to be max(1, firstNeighborIdx) because the result is at least 1. Then, we record the left neighbor index to a variable left. Then loop through the array, when seats[i] is 1, that means we find a right neighbor, so we calculate the result using case 1’s function. When we iterate to the last index, if the last seat is not empty, then we use case 1’s function as normal, but if last seat is empty, then we use case 3’s function to calculate the result. At the end, we return the maximum result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func maxDistToClosest(seats []int) int {
    i := 0
    for seats[i] != 1 { i += 1 }
    left := i
    res := max(1, left)
    i += 1

    for i < len(seats) {
        if i == len(seats) - 1 && seats[i] == 0 {
            res = max(res, i - left)
            break
        }
        if seats[i] == 1 {
            res = max(res, (i-left)/2)
            left = i
        }
        i += 1
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Number of Longest Increasing Subsequence

Given an integer array nums, return the number of longest increasing subsequences.

Example 1:

1
2
3
Input: nums = [1,3,5,4,7]
Output: 2
Explanation: The two longest increasing subsequences are [1, 3, 4, 7] and [1, 3, 5, 7].

Example 2:

1
2
3
Input: nums = [2,2,2,2,2]
Output: 5
Explanation: The length of longest continuous increasing subsequence is 1, and there are 5 subsequences' length is 1, so output 5.

Constraints:

  • 0 <= nums.length <= 2000

  • -10^6 <= nums[i] <= 10^6

Explanation

  1. Similar to 300. Longest Increasing Subsequence, we need an array sizeArr[i] represents the size of LIS and the LIS ends at index i. In this problem, we also need an array countArr[i] represents the number of LIS and the LIS ends at index i. Both elements in sizeArr and countArr are initialized to 1.

  2. Loop i from index 0 to the last index. Inner loop j from index 0 to index i exclusive. If nums[i] > nums[j] that means we find an increasing sequence. Then we check if sizeArr[i] < sizeArr[j] + 1 that means this is the first time we find an increasing sequence that ends at index i, so we update sizeArr[i] = sizeArr[j] + 1 and countArr[i] = countArr[j]. Else if sizeArr[i] == sizeArr[j] + 1 that means we find another j that also can build the LIS ending at index i, so we only update countArr[i] += countArr[j]. After the inner loop, we update the longestSize = max(longestSize, sizeArr[i].

  3. Outside the outtter loop, we iterate the sizeArr, if sizeArr[i] equals to longestSize, then we update our count res += countArr[i]. At the end, return the total count res.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func findNumberOfLIS(nums []int) int {
    res, longestSize := 0, 0
    sizeArr, countArr := make([]int, len(nums)), make([]int, len(nums))
    for i := range sizeArr {
        sizeArr[i] = 1
    }
    for i := range countArr {
        countArr[i] = 1
    }

    for i := 0; i < len(nums); i++ {
        for j := 0; j < i; j++ {
            if nums[i] > nums[j] {
                if sizeArr[j] + 1 > sizeArr[i] {
                    sizeArr[i] = sizeArr[j] + 1
                    countArr[i] = countArr[j]
                } else if sizeArr[j] + 1 == sizeArr[i] {
                    countArr[i] += countArr[j]
                }
            }
        }

        longestSize = max(longestSize, sizeArr[i])
    }

    for i := 0; i < len(nums); i++ {
        if sizeArr[i] == longestSize {
            res += countArr[i]
        }
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Recover Binary Search Tree

You are given the root of a binary search tree (BST), where exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Follow up: A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

Example 1:

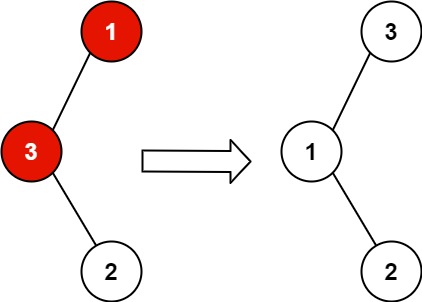
Recover Binary Search Tree

1
2
3
Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

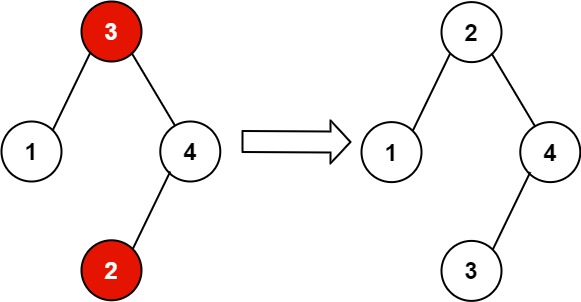
Example 2:

Recover Binary Search Tree

1
2
3
Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.

Constraints:

  • The number of nodes in the tree is in the range [2, 1000].

  • -2^31 <= Node.val <= 2^31 - 1

Explanation

  1. If we use O(n) space, we can use in-order traversal method to solve this problem. In a valid BST, if we use in-order traversal, all traversaled elements should be sorted, if it is not sorted, then this is not a valid BST.

  2. If the correct valid BST is [1, 2, 3, 4, 5, 6, 7, 8], if two elements are swaped mistake, let say 2 and 6 are swapped so we want to create two new variable to record 2 and 6, let say first and second, and now the traversal elements become [1, 6, 3, 4, 5, 2, 7, 8]. We find out 6 and 3 are not sorted in order (first is 6, second is 3), also 5 and 2 are not sorted in order (first remains 6, second is 2). So we swap first and second and we are done.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func recoverTree(root *TreeNode)  {
    pre, first, second := (*TreeNode)(nil), (*TreeNode)(nil), (*TreeNode)(nil)
    inorder(root, &pre, &first, &second)
    first.Val, second.Val = second.Val, first.Val
}

func inorder(root *TreeNode, pre, first, second **TreeNode) {
    if root == nil { return }
    inorder(root.Left, pre, first, second)

    if *pre != nil && (*pre).Val >= root.Val {
        if *first == nil {
            *first = *pre
        }
        *second = root
    }
    *pre = root

    inorder(root.Right, pre, first, second)
}