Problem

Given a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.

You should preserve the original relative order of the nodes in each of the two partitions.

Example:

1
2

Input: head = 1->4->3->2->5->2, x = 3
Output: 1->2->2->4->3->5

Problem

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.

Example:

1
2
3
4
5
6
7
8

Input:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
Output: 6

Problem

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

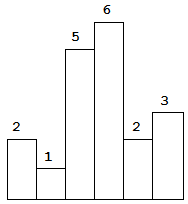
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

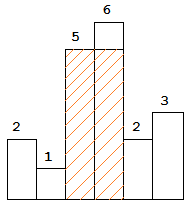
The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

1
2

Input: [2,1,5,6,2,3]
Output: 10

Problem

Given a sorted linked list, delete all duplicates such that each element appear only once.

Example 1:

1
2

Input: 1->1->2
Output: 1->2

Example 2:

1
2

Input: 1->1->2->3->3
Output: 1->2->3

Problem

Given a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list.

Example 1:

1
2

Input: 1->2->3->3->4->4->5
Output: 1->2->5

Example 2:

1
2

Input: 1->1->1->2->3
Output: 2->3

Problem

Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.

(i.e., [0,0,1,2,2,5,6] might become [2,5,6,0,0,1,2]).

You are given a target value to search. If found in the array return true, otherwise return false.

Example 1:

1
2

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2:

1
2

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Follow up:

• This is a follow up problem to Search in Rotated Sorted Array, where nums may contain duplicates.
• Would this affect the run-time complexity? How and why?

Problem

Given a sorted array nums, remove the duplicates in-place such that duplicates appeared at most twice and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Example 1:

1
2
3
4
5

Given nums = [1,1,1,2,2,3],

Your function should return length = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.

It doesn't matter what you leave beyond the returned length.

Example 2:

1
2
3
4
5

Given nums = [0,0,1,1,1,1,2,3,3],

Your function should return length = 7, with the first seven elements of nums being modified to 0, 0, 1, 1, 2, 3 and 3 respectively.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

1
2
3
4
5
6
7
8

// nums is passed in by reference. (i.e., without making a copy)
int len = removeDuplicates(nums);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

Problem

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example:

1
2
3
4
5
6
7
8
9
10

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

Problem

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

1
2
3
4
5
6
7
8
9
10
11
12

Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

Problem

Given two integers $n$ and $k$, return all possible combinations of $k$ numbers out of $1$ … $n$.

Example:

1
2
3
4
5
6
7
8
9
10

Input: n = 4, k = 2
Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]