Problem

Given a collection of intervals, merge all overlapping intervals.

Example 1:

1
2
3

Input: [[1,3],[2,6],[8,10],[15,18]]
Output: [[1,6],[8,10],[15,18]]
Explanation: Since intervals [1,3] and [2,6] overlaps, merge them into [1,6].

Example 2:

1
2
3

Input: [[1,4],[4,5]]
Output: [[1,5]]
Explanation: Intervals [1,4] and [4,5] are considered overlapping.

NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

Problem

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

Example 1:

1
2
3

Input: [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.

Example 2:

1
2
3
4

Input: [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum
             jump length is 0, which makes it impossible to reach the last index.

Problem

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

1
2
3
4
5
6
7

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

1
2
3
4
5
6
7

Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Problem

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

1
2
3

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

Problem

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

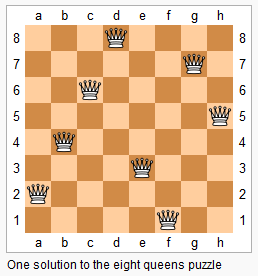
Given an integer n, return the number of distinct solutions to the n-queens puzzle.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

Input: 4
Output: 2
Explanation: There are two distinct solutions to the 4-queens puzzle as shown below.
[
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]

Problem

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

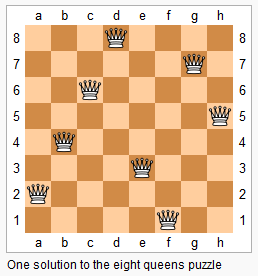
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens’ placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13

Input: 4
Output: [
 [".Q..",  // Solution 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // Solution 2
  "Q...",
  "...Q",
  ".Q.."]
]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.

Problem

Implement pow(x, n), which calculates $x$ raised to the power $n (x^n)$.

Example 1:

1
2

Input: 2.00000, 10
Output: 1024.00000

Example 2:

1
2

Input: 2.10000, 3
Output: 9.26100

Example 3:

1
2
3

Input: 2.00000, -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

Note:

• $-100.0 < x < 100.0$
• $n$ is a 32-bit signed integer, within the range [$−2^{31}$, $2^{31} − 1$]

Problem

Given an array of strings, group anagrams together.

Example:

1
2
3
4
5
6
7

Input: ["eat", "tea", "tan", "ate", "nat", "bat"],
Output:
[
  ["ate","eat","tea"],
  ["nat","tan"],
  ["bat"]
]

Note:

• All inputs will be in lowercase.
• The order of your output does not matter.

Problem

You are given an n x n 2D matrix representing an image.

Rotate the image by 90 degrees (clockwise).

Note:

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13

Given input matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

rotate the input matrix in-place such that it becomes:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Given input matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

rotate the input matrix in-place such that it becomes:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

Problem

Given a collection of numbers that might contain duplicates, return all possible unique permutations.

Example:

1
2
3
4
5
6
7

Input: [1,1,2]
Output:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]