Introduction

After praticing many LeetCode problems, I think it’s very important to summarize different patterns for the coding problems. I found out Grokking the Coding Interview: Patterns for Coding Questions explains very well, but some of the contents is not free, so I will refernce its free part, and also adding the problems that I found online and grouping them into the corresponding patterns.

Sliding Window

Find the average of all contiguous subarrays

In a coding problem, if we see words like “contiguous subarrays”, then we should think about solving it using sliding window. For example:

Given an array consisting of n integers, find the average of all contiguous subarray of given length k

Example:

Input:
Array: [1, 3, 2, 6, -1, 4, 1, 8, 2], K=5

Output:
[2.2, 2.8, 2.4, 3.6, 2.8]

Explanation

First, we want to create a sliding window. So, we create two pointers windowStart and windowEnd and they both initialize to 0.
We start iterate the windowEnd first, and in each iteration, we add the current number into the windowSum. Once the window length is equal to k, we calculate the average of the windowSum and add the average result to the result array, then subtract windowStart and move windowStart 1 step forward. Once windowEnd hit the end of iteration, we finish and return the result array.

Solution

import java.util.*;

class Main {
    public static double[] findAverages(int K, int[] arr) {
        double[] result = new double[arr.length - K + 1];
        double windowSum = 0;
        int windowStart = 0;
        for (int windowEnd = 0; windowEnd < arr.length; windowEnd++) {
            windowSum += arr[windowEnd];
            if (windowEnd >= K - 1) {
                result[windowStart] = windowSum / K;
                windowSum -= arr[windowStart];
                windowStart++;
            }
        }

        return result;
    }

    public static void main(String[] args) {
        double[] result = Main.findAverages(5, new int[] { 1, 3, 2, 6, -1, 4, 1, 8, 2 });
        System.out.println("Averages of subarrays of size K: " + Arrays.toString(result));
        // output
        // Averages of subarrays of size K: [2.2, 2.8, 2.4, 3.6, 2.8]
    }
}

Maximum Sum Subarray of Size K

Given an array of positive numbers and a positive number k, find the maximum sum of any contiguous subarray of size k.

Example 1:

Input: [2, 1, 5, 1, 3, 2], k=3
Output: 9
Explanation: Subarray with maximum sum is [5, 1, 3].

Input: [2, 3, 4, 1, 5], k=2
Output: 7
Explanation: Subarray with maximum sum is [3, 4].

Explanation

Using the sliding window technique. We iterate the windowEnd first, in each iteration, we add arr[windowEnd] to the windowSum. Start from windowEnd >= k-1, we updated the maximum result by max(res, windowSum), then subtract arr[windowStart] from the windowSum and move wndowStart 1 step forward.

Solution

class Main {
    public static int findMaxSumSubArray(int k, int[] arr) {
        int windowSum = 0, maxSum = 0;
        int windowStart = 0;
        for (int windowEnd = 0; windowEnd < arr.length; windowEnd++) {
            windowSum += arr[windowEnd];
            if (windowEnd >= k - 1) {
                maxSum = Math.max(maxSum, windowSum);
                windowSum -= arr[windowStart];
                windowStart++;
            }
        }

        return maxSum;
    }

    public static void main(String[] args) {
        System.out.println("Maximum sum of a subarray of size K: "
                + Main.findMaxSumSubArray(3, new int[] { 2, 1, 5, 1, 3, 2 }));
        System.out.println("Maximum sum of a subarray of size K: "
                + Main.findMaxSumSubArray(2, new int[] { 2, 3, 4, 1, 5 }));
        // output
        // Maximum sum of a subarray of size K: 9
        // Maximum sum of a subarray of size K: 7
    }
}

Smallest Subarray with a given sum

Given an array of positive numbers and a positive number ‘S’, find the length of the smallest contiguous subarray whose sum is greater than or equal to ‘S’. Return 0, if no such subarray exists.

Example 1:

Input: [2, 1, 5, 2, 3, 2], S=7
Output: 2
Explanation: The smallest subarray with a sum great than or equal to '7' is [5, 2].

Example 2:

Input: [2, 1, 5, 2, 8], S=7
Output: 1
Explanation: The smallest subarray with a sum greater than or equal to '7' is [8].

Example 3:

Input: [3, 4, 1, 1, 6], S=8
Output: 3
Explanation: Smallest subarrays with a sum greater than or equal to '8' are [3, 4, 1] or [1, 1, 6].

Explanation

Using the sliding window technique, in each iteration, we add the current number to the windowSum. While the windowSum is greater than or equal to S, we update the result, then subtract arr[windowStart] and move the windowStart 1 step forward.

Solution

class Main {
    public static int findMinSubArray(int S, int[] arr) {
        int windowSum = 0, minLength = Integer.MAX_VALUE;
        int windowStart = 0;
        for (int windowEnd = 0; windowEnd < arr.length; windowEnd++) {
            windowSum += arr[windowEnd];
            while (windowSum >= S) {
                minLength = Math.min(minLength, windowEnd - windowStart + 1);
                windowSum -= arr[windowStart];
                windowStart++;
            }
        }

        return minLength == Integer.MAX_VALUE ? 0 : minLength;
    }

    public static void main(String[] args) {
        int result = Main.findMinSubArray(7, new int[] { 2, 1, 5, 2, 3, 2 });
        System.out.println("Smallest subarray length: " + result);
        result = Main.findMinSubArray(7, new int[] { 2, 1, 5, 2, 8 });
        System.out.println("Smallest subarray length: " + result);
        result = Main.findMinSubArray(8, new int[] { 3, 4, 1, 1, 6 });
        System.out.println("Smallest subarray length: " + result);

        // output:
        // Smallest subarray length: 2
        // Smallest subarray length: 1
        // Smallest subarray length: 3
    }
}

Longest Substring with K Distinct Characters

Given a string, find the length of the longest substring in it with no more than K distinct characters.

Example 1:

Input: String="araaci", K=2
Output: 4
Explanation: The longest substring with no more than '2' distinct characters is "araa".

Example 2:

Input: String="araaci", K=1
Output: 2
Explanation: The longest substring with no more than '1' distinct characters is "aa".

Example 3:

Input: String="cbbebi", K=3
Output: 5
Explanation: The longest substrings with no more than '3' distinct characters are "cbbeb" & "bbebi".

Explanation

First, we need to create a character frequency character hashmap. Looping the input string character, we first update the character frequency hashmap. Then we check the size of the hashmap. While the hashmap has size more than K, we subtract 1 from the character str[windowStart]’s frequency’ in the hashmap, if updating its frequency, its frequency becomes 0, then we remove this character from the hashmap. Outside the while loop, we update the result max(res, windowEnd - windowStart + 1).

Solution

import java.util.*;

class Main {
    public static int findLength(String str, int k) {
        if (str == null || str.length() == 0 || str.length() < k)
            throw new IllegalArgumentException();

        int windowStart = 0, maxLength = 0;
        Map<Character, Integer> charFrequencyMap = new HashMap<>();
        for (int windowEnd = 0; windowEnd < str.length(); windowEnd++) {
            char rightChar = str.charAt(windowEnd);
            charFrequencyMap.put(rightChar, charFrequencyMap.getOrDefault(rightChar, 0) + 1);
            while (charFrequencyMap.size() > k) {
                char leftChar = str.charAt(windowStart);
                charFrequencyMap.put(leftChar, charFrequencyMap.get(leftChar) - 1);
                if (charFrequencyMap.get(leftChar) == 0) {
                    charFrequencyMap.remove(leftChar);
                }
                windowStart++;
            }
            maxLength = Math.max(maxLength, windowEnd - windowStart + 1);
        }

        return maxLength;
    }

    public static void main(String[] args) {
        System.out.println("Length of the longest substring: " + Main.findLength("araaci", 2));
        System.out.println("Length of the longest substring: " + Main.findLength("araaci", 1));
        System.out.println("Length of the longest substring: " + Main.findLength("cbbebi", 3));

        // output:
        // Length of the longest substring: 4
        // Length of the longest substring: 2
        // Length of the longest substring: 5
    }
}

LeetCode 904. Fruit Into Baskets

In a row of trees, the i-th tree produces fruit with type tree[i].

You start at any tree of your choice, then repeatedly perform the following steps:

Add one piece of fruit from this tree to your baskets. If you cannot, stop.
Move to the next tree to the right of the current tree. If there is no tree to the right, stop.

Note that you do not have any choice after the initial choice of starting tree: you must perform step 1, then step 2, then back to step 1, then step 2, and so on until you stop.

You have two baskets, and each basket can carry any quantity of fruit, but you want each basket to only carry one type of fruit each.

What is the total amount of fruit you can collect with this procedure?

Example 1:

Input: [1,2,1]
Output: 3
Explanation: We can collect [1,2,1].

Example 2:

Input: [0,1,2,2]
Output: 3
Explanation: We can collect [1,2,2].
If we started at the first tree, we would only collect [0, 1].

Example 3:

Input: [1,2,3,2,2]
Output: 4
Explanation: We can collect [2,3,2,2].
If we started at the first tree, we would only collect [1, 2].

Example 4:

Input: [3,3,3,1,2,1,1,2,3,3,4]
Output: 5
Explanation: We can collect [1,2,1,1,2].
If we started at the first tree or the eighth tree, we would only collect 4 fruits.

Note:

1. 1 <= tree.length <= 40000
2. 0 <= tree[i] < tree.length

Explanation

We can use sliding window technique to solve this problem. First, since we can only have 2 fruit types, so we need to create a hashmap, the key is fruit type, the value is its frequency. While the hashmap has key size more than 2, then we need to subtract tree[windowStart]’s frequency and move windowStart 1 step forward. After the while loop, we can count how many fruit we pick by windowEnd - windowStart + 1.

Solution

class Solution {
    public int totalFruit(int[] tree) {
        int res = 0, windowStart = 0;
        Map<Integer, Integer> hm = new HashMap<>();
        for (int windowEnd = 0; windowEnd < tree.length; windowEnd++) {
            hm.put(tree[windowEnd], hm.getOrDefault(tree[windowEnd], 0) + 1);
            while (hm.size() > 2) {
                int leftTree = tree[windowStart];
                hm.put(leftTree, hm.get(leftTree) - 1);
                if (hm.get(leftTree) == 0) {
                    hm.remove(leftTree);
                }
                windowStart += 1;
            }
            res = Math.max(res, windowEnd - windowStart + 1);
        }

        return res;
    }
}

LeetCode 3. Longest Substring Without Repeating Characters

Given a string, find the length of the longest substring without repeating characters.

Example 1:

Input: "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

Example 2:

Input: "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3:

Input: "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
             Note that the answer must be a substring, "pwke" is a subsequence and not a substring.

Explanation

We can also solve this problem using sliding window technique. Think of we will maintain a window that contains all unique characters. First initialize windowStart and windowEnd to 0. Also, initialize a hashset to record the window’s unique characters.
Loop the windowEnd from index 0 to the last index of the input string. While the set contains the current iterated character, we remove the window’s left character str[windowStart] and move windowStart 1 step forward, repeat this while loop until the set doesn’t contains the incoming iterated character. Next, we add the iterated character into the set, then calculate the result be max(res, windowEnd - windowStart + 1).

Solution

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int windowStart = 0, res = 0;
        Set<Character> set = new HashSet<>();

        for (int windowEnd = 0; windowEnd < s.length(); windowEnd++) {
            char cur = s.charAt(windowEnd);
            while (set.contains(cur)) {
                char windowLeft = s.charAt(windowStart);
                set.remove(windowLeft);
                windowStart += 1;
            }
            set.add(cur);
            res = Math.max(res, windowEnd - windowStart + 1);
        }

        return res;
    }
}

LeetCode 424. Longest Repeating Character Replacement

Given a string s that consists of only uppercase English letters, you can perform at most k operations on that string.

In one operation, you can choose any character of the string and change it to any other uppercase English character.

Find the length of the longest sub-string containing all repeating letters you can get after performing the above operations.

Note: Both the string’s length and k will not exceed 10^4.

Example 1:

Input:
s = "ABAB", k = 2

Output:
4

Explanation:
Replace the two 'A's with two 'B's or vice versa.

Example 2:

Input:
s = "AABABBA", k = 1

Output:
4

Explanation:
Replace the one 'A' in the middle with 'B' and form "AABBBBA".
The substring "BBBB" has the longest repeating letters, which is 4.

Explanation

We can use Sliding Window technique to solve this problem. First think of if there is no restriction of k, and we need to find the minimum number of replacement to form a string that is made of only 1 character. To solve this, we use the length of the string subtract the maximum frequency of a character. Now, if we have k, then we are looking for substring’s length subtract the maximum frequency of characters in this substring, and the difference is less than or equals to k. We need to return the maximum length of this substring. The substring is like a window.
Initialize windowStart = 0. Loop windowEnd from the beginning character to the last character, the window’s length is windowEnd - windowStart + 1. In each iteration, we increase the frequency of the iterated character. Then, we update the maxCnt which is the maximum frequency. Because of the limitation of k, while the window length subtract the maximum frequency maxCnt is greater than k, we need to increase windowStart by 1 so that this iteration’s window length is equals to the last iteration’s window length, also we update the frequency of the character arr[windowStart] by subtract 1. We are not changing the maxCnt because we want the window length be as large as possible, so if maxCnt is greater, then the number of characters we are going to change will be smaller, in other words, the window length will be larger. Outside the while loop, we update the maximum of the window length res = max(res, windowEnd-windowStart+1).
For example, if the input string is zzzabc and k = 1. When we iterate to index 3, the maxCnt = 3, the window length windowEnd - windowStart + 1 = 4, windowEnd - windowStart + 1 - maxCnt = 4 - 3 = 1 which is not greater than k, so we skip the while loop, and update the result be windowEnd - windowStart + 1 = 4. When we iterate to index 4, since windowEnd - windowStart + 1 = 5, and 5 - 3 = 2 > k, we increase windowStart, so this time the window length is same as the last iteration which is 4. So we are keeping the maximum window length be maxCnt + i where i <= k.

Solution

class Solution {
    public int characterReplacement(String s, int k) {
        int res = 0, windowStart = 0;
        int maxCount = 0;
        int[] freq = new int[26];

        for (int windowEnd = 0; windowEnd < s.length(); windowEnd++) {
            char cur = s.charAt(windowEnd);
            freq[cur - 'A'] += 1;
            maxCount = Math.max(maxCount, freq[cur - 'A']);
            while (windowEnd - windowStart + 1 - maxCount > k) {
                freq[s.charAt(windowStart) - 'A'] -= 1;
                windowStart += 1;
            }
            res = Math.max(res, windowEnd - windowStart + 1);
        }

        return res;
    }
}

LeetCode 1004. Max Consecutive Ones III

Given an array A of 0s and 1s, we may change up to K values from 0 to 1.

Return the length of the longest (contiguous) subarray that contains only 1s.

Example 1:

Input: A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
Output: 6
Explanation:
[1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1.  The longest subarray is underlined.

Example 2:

Input: A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
Output: 10
Explanation:
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
Bolded numbers were flipped from 0 to 1.  The longest subarray is underlined.

Note:

1 <= A.length <= 20000
0 <= K <= A.length
A[i] is 0 or 1

Explanation

We can use sliding window technique to solve this problem. Think of the window is the valid subarray that contains 1s and number of 0s less than or equal to K. First, we should create a variable cnt0 to count how many 0s. Loop windowEnd to the end of array, for each iteration, we update cnt0 first. While cnt0 > K, then we try to slide the windowStart forward. First, if A[windowStart] is 0, we decrease cnt0. Then we move windowStart 1 step forward. Repeat this while loop until cnt0 <= K. Outside the while loop, we update the result be max(res, windowEnd - windowStart + 1).

Solution

class Solution {
    public int longestOnes(int[] A, int K) {
        int res = 0, cnt0 = 0;
        int windowStart = 0;

        for (int windowEnd = 0; windowEnd < A.length; windowEnd++) {
            if (A[windowEnd] == 0) {
                cnt0 += 1;
            }
            while (cnt0 > K) {
                if (A[windowStart] == 0) {
                    cnt0 -= 1;
                }
                windowStart += 1;
            }
            res = Math.max(res, windowEnd - windowStart + 1);
        }

        return res;
    }
}

Two Pointers

Pair with Target Sum

Given an array and a integer sum. Print all pairs that satisify each pair sum to sum.

Does array contains only positive or negative numbers?

Array contains only positive number.
What if the same pair repeats twice, should we print it every time?

Yes, as long as the number have not been used.
Is reverse of pair is acceptable e.g. can we print both (4,1) and (1,4) if given sum is 5.

No.
Does (3, 3) is a valid pair forgiven sum of 6?

Yes, as long as there are two 3s.
How big the array is?

Bigger than computer ram.

Explanation

Since the array is bigger than computer ram, we cannot use HashMap to store the array. To solve this, we can use two pointer technique. First, we sort the array. Initialize one pointer at the first index, another pointer at the last index. If the two values both pointers point at sum to sum, then we print the these two numbers, then we increase the left pointer and decrease the right pointer. Else if the two values both pointers point at less than sum, then we increase left pointer. Else the values both pointers point at greater than sum, then we decrease the right pointer.

Solution

import java.util.*;

class Main {
    static void solve(int[] arr, int sum) {
        Arrays.sort(arr);
        int left = 0, right = arr.length - 1;

        while (left < right) {
            if (arr[left] + arr[right] == sum) {
                System.out.printf("%d %d\n", arr[left], arr[right]);
                left += 1;
                right -= 1;
            } else if (arr[left] + arr[right] < sum) {
                left += 1;
            } else {
                right -= 1;
            }
        }
    }

    // output
    // 2 4
    // 2 4
    // 3 3

    // static void solve(int[] arr, int sum) {
    //     Map<Integer, Integer> hm = new HashMap();

    //     for (int num : arr) {
    //         int target = sum - num;
    //         if (!hm.containsKey(target)) {
    //             hm.put(num, hm.getOrDefault(num, 0) + 1);
    //         } else {
    //             System.out.printf("%d %d\n", num, target);
    //             hm.put(target, hm.get(target) - 1);
    //             if (hm.get(target) == 0) {
    //                 hm.remove(target);
    //             }
    //         }
    //     }
    // }

    // output
    // 4 2
    // 4 2
    // 3 3

    public static void main (String[] args) {
        int[] arr = new int[] {2, 2, 4, 4, 3, 3};
        solve(arr, 6);
    }
}

LeetCode 26. Remove Duplicates from Sorted Array

Given a sorted array nums, remove the duplicates in-place such that each element appear only once and return the new length.

Do not allocate extra space for another array, you must do this by modifying the input array in-place with O(1) extra memory.

Example 1:

Given nums = [1,1,2],

Your function should return length = 2, with the first two elements of nums being 1 and 2 respectively.

It doesn't matter what you leave beyond the returned length.

Example 2:

Given nums = [0,0,1,1,1,2,2,3,3,4],

Your function should return length = 5, with the first five elements of nums being modified to 0, 1, 2, 3, and 4 respectively.

It doesn't matter what values are set beyond the returned length.

Clarification:

Confused why the returned value is an integer but your answer is an array?

Note that the input array is passed in by reference, which means modification to the input array will be known to the caller as well.

Internally you can think of this:

// nums is passed in by reference. (i.e., without making a copy)
int len = removeDuplicates(nums);

// any modification to nums in your function would be known by the caller.
// using the length returned by your function, it prints the first len elements.
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

Explanation

We can create two pointers, the current pointer is pointing at the end of the non-duplicated result array, the fast pointer is iterating every element of the array.
Initialize the current pointer at index 0, the fast pointer at index 1. If the fast pointer and current pointer have the same value, then faster pointer move forward. Else, the current pointer’s index + 1 is set to the fast pointer’s value. Iterating until the fast pointer hits the end of the array.
At the end, the length will be current pointer index + 1.

Solution

class Solution {
    public int removeDuplicates(int[] nums) {
        int curPointer = 0;
        for (int fastPointer = 1; fastPointer < nums.length; fastPointer++) {
            if (nums[fastPointer] != nums[curPointer]) {
                nums[++curPointer] = nums[fastPointer];
            }
        }
        return curPointer+1;
    }
}

LeetCode 977. Squares of a Sorted Array

Given an array of integers A sorted in non-decreasing order, return an array of the squares of each number, also in sorted non-decreasing order.

Example 1:

Input: [-4,-1,0,3,10]
Output: [0,1,9,16,100]

Example 2:

Input: [-7,-3,2,3,11]
Output: [4,9,9,49,121]

Note:

1 <= A.length <= 10000
-10000 <= A[i] <= 10000
A is sorted in non-decreasing order.

Explanation

First, we need to use a for loop to find out the minimum absolue value’s index, and we named this index minAbsoluteIndex. Then we make a left pointer points to minAbsoluteIndex, and a right pointer points to minAbsoluteIndex + 1. But if the minAbsoluteIndex is the last index, then we make left pointer be minAbsoluteIndex - 1, right pointer be minAbsoluteIndex.
While the leftPtr >= 0 and rightPtr < n, we compare the absolue value of both pointed value in the array. If the left pointer’s absolute value is smaller, then we calculate its square and put into the result array and move leftPtr to the 1 step left. Else we put the right poitner’s value’s square into the result array and move rightPtr 1 step right. Repeat this while loop until one of the pointer is out of bound. Then we put the non out of bound pointer’s value’s square into result.
We can also first find out if the first number of the input array is equal or greater than 0, then we simply one loop and each iteration we put the square of the iterated number into the result array. If the last number of the input array is negative, then we simply loop from right to left and each iteration, we put the iterated number’s square into the array. Else, the minAbsoluteIndex is the index of the first non-negative number.

Solution

class Solution {
    public int[] sortedSquares(int[] A) {
        if (A == null || A.length == 0) return new int[0];
        int n = A.length;
        int[] res = new int[n];
        int minAbsoluteIndex = 0;
        int leftPtr = 0, rightPtr = 0;

        for (int i = 0; i < n; i++) {
            if (Math.abs(A[i]) < Math.abs(A[minAbsoluteIndex])) {
                minAbsoluteIndex = i;
            }
        }
        if (minAbsoluteIndex == n-1) {
            rightPtr = minAbsoluteIndex;
            leftPtr = rightPtr - 1;
        } else {
            leftPtr = minAbsoluteIndex;
            rightPtr = leftPtr + 1;
        }

        int ind = 0;
        while (leftPtr >= 0 && rightPtr < n) {
            if (Math.abs(A[leftPtr]) < Math.abs(A[rightPtr])) {
                res[ind++] = A[leftPtr] * A[leftPtr];
                leftPtr -= 1;
            } else {
                res[ind++] = A[rightPtr] * A[rightPtr];
                rightPtr += 1;
            }
        }
        while (leftPtr >= 0) {
            res[ind++] = A[leftPtr] * A[leftPtr];
            leftPtr -= 1;
        }
        while (rightPtr < n) {
            res[ind++] = A[rightPtr] * A[rightPtr];
            rightPtr += 1;
        }

        return res;
    }
}

LeetCode 15. 3Sum

Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

Note:

The solution set must not contain duplicate triplets.

Example:

Given array nums = [-1, 0, 1, 2, -1, -4],

A solution set is:
[
  [-1, 0, 1],
  [-1, -1, 2]
]

Explanation

Sort the array.
If the first element is greater than 0 or the last element is less than 0, we know that we can’t form a 0.
Loop through the array start from the first element, we fix the first element, then use two pointers technique to find two elements that sum to targetVal-fixVal until break out the left < right condition. While looping, we need to ignore the same fix number and left and right values.

Solution

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        Arrays.sort(nums);
        if (nums.length == 0 || nums[0] > 0 || nums[nums.length-1] < 0) {
            return res;
        }
        List<Integer> lst = new ArrayList<>();
        for (int i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i] == nums[i-1]) {
                continue;
            }
            int fix = nums[i];
            int target = 0 - fix;
            int left = i + 1;
            int right = nums.length-1;
            while(left < right) {
                if (nums[left] + nums[right] == target) {
                    res.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    while (left < right && nums[left] == nums[left+1]) {
                        left++;
                    }
                    while (left < right && nums[right] == nums[right-1]) {
                        right--;
                    }
                    left++;
                    right--;
                } else if (nums[left] + nums[right] < target) {
                    left++;
                } else {
                    right--;
                }
            }
        }
        return res;
    }
}

LeetCode 16. 3Sum Closest

Given an array nums of n integers and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution.

Example:

Given array nums = [-1, 2, 1, -4], and target = 1.

The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).

Explanation

Similar to 15. 3Sum, first, sort the array. We need to fix one number, then use two pointers technique to find the sum of 3 elements, and compare the sum with the target to get the newDiff. Since we are looking for the closest sum, we need to define a diff variable as the minimum diff. In other words, if newDiff is less than diff, then update diff to newDiff. Note, we should use absolute value to find newDiff.

Solution

class Solution {
    public int threeSumClosest(int[] nums, int target) {
        if (nums == null || nums.length < 3) return -1;
        int res = nums[0] + nums[1] + nums[2];
        int diff = Math.abs(target - res);
        Arrays.sort(nums);
        for (int fixInd = 0; fixInd < nums.length-2; fixInd++) {
            int i = fixInd + 1;
            int j = nums.length - 1;
            while (i < j) {
                int sum = nums[fixInd] + nums[i] + nums[j];
                int newDiff = Math.abs(target - sum);
                if (newDiff < diff) {
                    diff = newDiff;
                    res = sum;
                }
                if (sum < target) {
                    i += 1;
                } else if (sum > target) {
                    j -= 1;
                } else {
                    return target;
                }
            }
        }

        return res;
    }
}

LeetCode 259. 3Sum Smaller

Given an array of n integers nums and a target, find the number of index triplets i, j, k with 0 <= i < j < k < n that satisfy the condition nums[i] + nums[j] + nums[k] < target.

Example:

Input: nums = [-2,0,1,3], and target = 2
Output: 2
Explanation: Because there are two triplets which sums are less than 2:
             [-2,0,1]
             [-2,0,3]

Follow up: Could you solve it in $O(n^2)$ runtime?

Explanation

Sort the array, then apply the two pointers technique.
Loop i from 0 to arr.length - 2. Inside the loop, initialize left = i + 1 and right = arr.length - 1. While left < right, we can calculate the triplet sum be nums[i] + nums[left] + nums[right]. If the sum is greater or equal than the target, we move the right poitner 1 step left. Else, we can calculate the number of triplet sum less than target using right - left. Then we move the left pointer 1 step forward.

Solution

class Solution {
    public int threeSumSmaller(int[] nums, int target) {
        int res = 0;
        if (nums.length < 3) return res;
        Arrays.sort(nums);
        for (int i = 0; i < nums.length - 2; i++) {
            int left = i + 1;
            int right = nums.length - 1;
            while (left < right) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum >= target) {
                    right -= 1;
                } else {
                    res += right - left;
                    left += 1;
                }
            }
        }

        return res;
    }
}

LeetCode 713. Subarray Product Less Than K

Your are given an array of positive integers nums.

Count and print the number of (contiguous) subarrays where the product of all the elements in the subarray is less than k.

Example 1:

Input: nums = [10, 5, 2, 6], k = 100
Output: 8
Explanation: The 8 subarrays that have product less than 100 are: [10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6].
Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.

Note:

0 < nums.length <= 50000.
0 < nums[i] < 1000.
0 <= k < 10^6.

Explanation

Since this is a subarray problem, we can think of using sliding window technique or two pointers (slow, fast pointers) technique. In this problem, we will use two pointers technique.
If k less than or equal to 1, we will return 0 since all elements in the input array are positive. We initialize slow = 0 and fast = 0. Loop fast from 0 to the last index of the input array, we can think of fast be the last element of the subarray, slow be the first element of the subarray. In each iteration, we calculate the production by prod *= nums[fast]. If prod < k, we can count the number of subarray be fast - slow + 1. Else, while prod >= k, we need to update prod /= nums[slow] and move slow 1 step forward.

Solution

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        int res = 0;
        if (k <= 1) return res;
        int prod = 1;
        int slow = 0;
        for (int fast = 0; fast < nums.length; fast++) {
            prod *= nums[fast];
            while (prod >= k) {
                prod /= nums[slow];
                slow += 1;
            }
            res += fast - slow + 1;
        }

        return res;
    }
}

LeetCode 75. Sort Colors

Given an array with n objects colored red, white or blue, sort them in-place so that objects of the same color are adjacent, with the colors in the order red, white and blue.

Here, we will use the integers 0, 1, and 2 to represent the color red, white, and blue respectively.

Note: You are not suppose to use the library’s sort function for this problem.

Example

Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

Follow up:

A rather straight forward solution is a two-pass algorithm using counting sort. First, iterate the array counting number of 0’s, 1’s, and 2’s, then overwrite array with total number of 0’s, then 1’s and followed by 2’s.
Could you come up with a one-pass algorithm using only constant space?

Explanation

This problem is also called Dutch national flag sorting problem. We can solve this problem using two pointer technique. First, initialize a left pointer points at the next index of the placeholder of 0, right points at the previous index of the placeholder of 2. In other words, left = 0 and right = arr.length - 1.
Loop though the mid pointer as long as it’s not greater than right. In other words, while mid <= right.
If the current element arr[mid] is 2, then we swap current element with arr[right] and decrease right.
Else if the current element arr[mid] is 0, then we swap current element with arr[left] and increase left and mid.
Else if the current element is 1, then we increase mid.

Solution

class Solution {
    void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

    public void sortColors(int[] nums) {
        int left = 0, right = nums.length - 1;
        int mid = 0;
        while (mid <= right) {
            if (nums[mid] == 2) {
                swap(nums, mid, right);
                right -= 1;
            } else if (nums[mid] == 0) {
                swap(nums, left, mid);
                left += 1;
                mid += 1;
            } else if (nums[mid] == 1) {
                mid += 1;
            }
        }
    }
}

Fast & Slow pointers

LeetCode 141. Linked List Cycle

Given a linked list, determine if it has a cycle in it.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the second node.

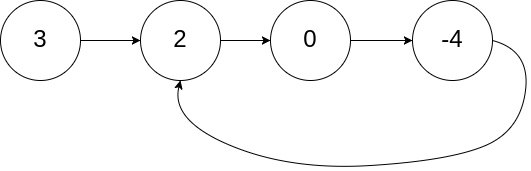
Example 2:

Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where tail connects to the first node.

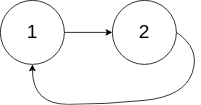
Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Follow up:

Can you solve it using $O(1)$ (i.e. constant) memory?

Explanation

Both fast and slow pointers points to the head.
When fast pointer moves two steps, slow pointer move one step.
If fast pointer hits null, then no cycle; else if slow pointer and fast pointer point to the same node, then there’s cycle.

Solution

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) return false;
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) return true;
        }
        return false;
    }
}

LeetCode 142. Linked List Cycle II

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

To represent a cycle in the given linked list, we use an integer pos which represents the position (0-indexed) in the linked list where tail connects to. If pos is -1, then there is no cycle in the linked list.

Note: Do not modify the linked list.

Example 1:

Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Follow-up:

Can you solve it without using extra space?

Explanation

Both slow and fast pointers point to the head.
While fast and fast.next is not null, when slow pointer moves one step, fast pointer moves two steps.
If slow pointer and fast pointer points to the same node, then it means there’s cycle, break out of the while loop.
When out of the while loop, we check if slow pointer and fast pointer point to the same node. If they are not point to the same node, that means fast pointer hit to the end, so we return NULL.
Now, fast pointer moves back to the head. slow pointer doesn’t move.
Then run both, slow pointer and fast pointer at the same speed, the point the meet is the entry of cycle.

Solution

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if (head == null || head.next == null) {
            return null;
        }
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if (slow == fast) break;
        }
        if (slow != fast) return null;
        fast = head;
        while (slow != fast) {
            slow = slow.next;
            fast = fast.next;
        }
        return slow;
    }
}

LeetCode 202. Happy Number

Write an algorithm to determine if a number is “happy”.

A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers.

Example:

Input: 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

Explanation

We can also use two pointer technique to solve this problem. Similar to 141. Linked List Cycle. The difference is in this problem, the cycle must exist. Slow will be the sum of the digit square, in other words, slow=cal(slow), fast will be fast=cal(cal(fast)). When slow is equals to fast, we break out the loop, and check if slow is equals to 1. If it’s 1, we return true; else return false.

Solution

class Solution {
    int calc(int num) {
        int res = 0;
        while (num > 0) {
            res += (num % 10) * (num % 10);
            num /= 10;
        }
        return res;
    }

    public boolean isHappy(int n) {
        int slow = n, fast = n;
        while (true) {
            slow = calc(slow);
            fast = calc(fast);
            fast = calc(fast);
            if (slow == fast) break;
        }
        return slow == 1;
    }
}

LeetCode 876. Middle of the Linked List

Given a non-empty, singly linked list with head node head, return a middle node of linked list.

If there are two middle nodes, return the second middle node.

Example 1:

Input: [1,2,3,4,5]
Output: Node 3 from this list (Serialization: [3,4,5])
The returned node has value 3.  (The judge's serialization of this node is [3,4,5]).
Note that we returned a ListNode object ans, such that:
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, and ans.next.next.next = NULL.

Example 2:

Input: [1,2,3,4,5,6]
Output: Node 4 from this list (Serialization: [4,5,6])
Since the list has two middle nodes with values 3 and 4, we return the second one.

Note:

The number of nodes in the given list will be between 1 and 100.

Explanation

We can use slow and fast pointer to solve this problem. First initalize slow and fast pointers both point at the input head node. While fast pointer and fast.next are not NULL, then slow pointer move 1 step forward, fast pointer move 2 step forward. Outside of the while loop, that means fast pointer either hit the last node or the last.next node. At the same time, slow pointer is pointing the second middle node.

Solution

 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode middleNode(ListNode head) {
        ListNode slow = head, fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }
}

Merge Intervals

Given a list of intervals, merge all the overlapping intervals to produce a list that has only mutually exclusive intervals.

Example 1:

Intervals: [[1,4], [2,5], [7,9]]
Output: [[1,5], [7,9]]
Explanation: Since the first two intervals [1,4] and [2,5] overlap, we merged them into one [1,5].

Example 2:

Intervals: [[6,7], [2,4], [5,9]]
Output: [[2,4], [5,9]]
Explanation: Since the intervals [6,7] and [5,9] overlap, we merged them into one [5,9].

Example 3:

Intervals: [[1,4], [2,6], [3,5]]
Output: [[1,6]]
Explanation: Since all the given intervals overlap, we merged them into one.

Explanation

Sort the interval by their start time. Put the early start time in the beginning.
If a overlaps b (i.e. b.start <= a.end), we need to merge them into a new interval c such that:
1
2
c.start = a.start c.end = max(a.end, b.end)
Initialize the first interval be the interval that we want to compare with, let’s named it myInterval. Start looping from the second interval to compare with myInterval. If the iterated interval cannot merge with myInterval, then we add myInterval into the result list, else we merge the iterated interval with myInterval and named the merge interval myInterval.

Solution

import java.util.*;

class Interval {
  int start;
  int end;

  public Interval(int start, int end) {
    this.start = start;
    this.end = end;
  }
};

class MergeIntervals {
  public static List<Interval> merge(List<Interval> intervals) {
    if (intervals.size() < 2) return intervals;

    List<Interval> mergedIntervals = new LinkedList<Interval>();
    Collections.sort(intervals, (a, b) -> Integer.compare(a.start, b.start));

    Interval myInterval = intervals.get(0);
    for (int i = 1; i < intervals.size(); i++) {
      if (myInterval.end < intervals.get(i).start) {
        mergedIntervals.add(myInterval);
        myInterval = intervals.get(i);
      } else {
        myInterval.start = myInterval.start;
        myInterval.end = Math.max(myInterval.end, intervals.get(i).end);
      }
    }
    mergedIntervals.add(myInterval);

    return mergedIntervals;
  }

  public static void main(String[] args) {
    List<Interval> input = new ArrayList<Interval>();
    input.add(new Interval(1, 4));
    input.add(new Interval(2, 5));
    input.add(new Interval(7, 9));
    System.out.print("Merged intervals: ");
    for (Interval interval : MergeIntervals.merge(input))
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();

    input = new ArrayList<Interval>();
    input.add(new Interval(6, 7));
    input.add(new Interval(2, 4));
    input.add(new Interval(5, 9));
    System.out.print("Merged intervals: ");
    for (Interval interval : MergeIntervals.merge(input))
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();

    input = new ArrayList<Interval>();
    input.add(new Interval(1, 4));
    input.add(new Interval(2, 6));
    input.add(new Interval(3, 5));
    System.out.print("Merged intervals: ");
    for (Interval interval : MergeIntervals.merge(input))
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();
  }
}

// output:
// Merged intervals: [1,5] [7,9]
// Merged intervals: [2,4] [5,9]
// Merged intervals: [1,6]

Insert Interval

Given a list of non-overlapping intervals sorted by their start time, insert a given interval at the correct position and merge all necessary intervals to produce a list that has only mutually exclusive intervals.

Example 1:

Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,6]
Output: [[1,3], [4,7], [8,12]]
Explanation: After insertion, since [4,6] overlaps with [5,7], we merged them into one [4,7].

Example 2:

Input: Intervals=[[1,3], [5,7], [8,12]], New Interval=[4,10]
Output: [[1,3], [4,12]]
Explanation: After insertion, since [4,10] overlaps with [5,7] & [8,12], we merged them into [4,12].

Example 3:

Input: Intervals=[[2,3],[5,7]], New Interval=[1,4]
Output: [[1,4], [5,7]]
Explanation: After insertion, since [1,4] overlaps with [2,3], we merged them into one [1,4].

Explanation

Adding all intervals that’s ending before the new interval’s start to the result list.
When the iterated interval’s ending is greater than the new interval’s start, we need to merge the iterated interval with the new interval and we think of it as the new interval. Repeat this step while the iterated interval’s start is less than or equal to the new interval’s end.
Add the rest of the iterated interval into the result list.

Solution

import java.util.*;

class Interval {
  int start;
  int end;

  public Interval(int start, int end) {
    this.start = start;
    this.end = end;
  }
};

class InsertInterval {

  public static List<Interval> insert(List<Interval> intervals, Interval newInterval) {
    if (intervals == null || intervals.isEmpty())
      return Arrays.asList(newInterval);

    List<Interval> mergedIntervals = new ArrayList<>();

    int i = 0;
    // skip (and add to output) all intervals that come before the 'newInterval'
    while (i < intervals.size() && intervals.get(i).end < newInterval.start)
      mergedIntervals.add(intervals.get(i++));

    // merge all intervals that overlap with 'newInterval'
    while (i < intervals.size() && intervals.get(i).start <= newInterval.end) {
      newInterval.start = Math.min(intervals.get(i).start, newInterval.start);
      newInterval.end = Math.max(intervals.get(i).end, newInterval.end);
      i++;
    }

    // insert the newInterval
    mergedIntervals.add(newInterval);

    // add all the remaining intervals to the output
    while (i < intervals.size())
      mergedIntervals.add(intervals.get(i++));

    return mergedIntervals;
  }

  public static void main(String[] args) {
    List<Interval> input = new ArrayList<Interval>();
    input.add(new Interval(1, 3));
    input.add(new Interval(5, 7));
    input.add(new Interval(8, 12));
    System.out.print("Intervals after inserting the new interval: ");
    for (Interval interval : InsertInterval.insert(input, new Interval(4, 6)))
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();

    input = new ArrayList<Interval>();
    input.add(new Interval(1, 3));
    input.add(new Interval(5, 7));
    input.add(new Interval(8, 12));
    System.out.print("Intervals after inserting the new interval: ");
    for (Interval interval : InsertInterval.insert(input, new Interval(4, 10)))
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();

    input = new ArrayList<Interval>();
    input.add(new Interval(2, 3));
    input.add(new Interval(5, 7));
    System.out.print("Intervals after inserting the new interval: ");
    for (Interval interval : InsertInterval.insert(input, new Interval(1, 4)))
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();
  }
}

// output:
// Intervals after inserting the new interval: [1,3] [4,7] [8,12]
// Intervals after inserting the new interval: [1,3] [4,12]
// Intervals after inserting the new interval: [1,4] [5,7]

Intervals Intersection

Given two lists of intervals, find the intersection of these two lists. Each list consists of disjoint intervals sorted on their start time.

Example 1:

Input: arr1=[[1, 3], [5, 6], [7, 9]], arr2=[[2, 3], [5, 7]]
Output: [2, 3], [5, 6], [7, 7]
Explanation: The output list contains the common intervals between the two lists.

Example 2:

Input: arr1=[[1, 3], [5, 7], [9, 12]], arr2=[[5, 10]]
Output: [5, 7], [9, 10]
Explanation: The output list contains the common intervals between the two lists.

Explanation

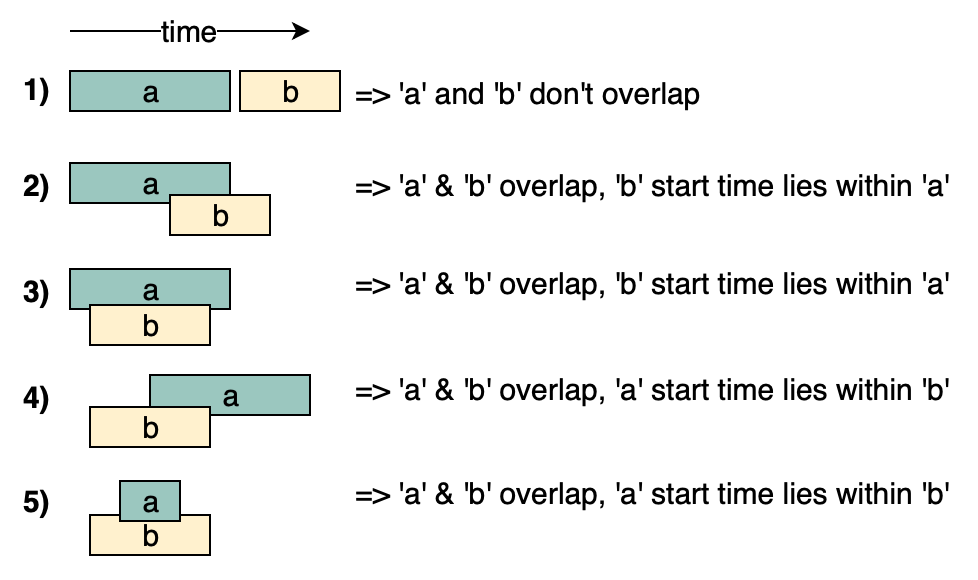
There are four scenarios when the two intervals overlap (2-5). Whenever the two intervals overlap, one of the interval’s start time lies within the other interval.

The overlapping interval will be equal to:

 start = max(a.start, b.start)
 end = min(a.end, b.end)

After checking if two intervals intersect, we move the index of the interval that has ending pointer smaller forward 1 step. When the index is greater than the corresponding size of the array, we finish and return the result.

Solution

import java.util.*;

class Interval {
  int start;
  int end;

  public Interval(int start, int end) {
    this.start = start;
    this.end = end;
  }
};

class IntervalsIntersection {

  public static Interval[] merge(Interval[] arr1, Interval[] arr2) {
    List<Interval> result = new ArrayList<Interval>();
    int i = 0, j = 0;
    while (i < arr1.length && j < arr2.length) {
      // check if the interval arr[i] intersects with arr2[j]
      // check if one of the interval's start time lies within the other interval
      if ((arr1[i].start >= arr2[j].start && arr1[i].start <= arr2[j].end)
          || (arr2[j].start >= arr1[i].start && arr2[j].start <= arr1[i].end)) {
        // store the intersection part
        result.add(new Interval(Math.max(arr1[i].start, arr2[j].start), Math.min(arr1[i].end, arr2[j].end)));
      }

      // move next from the interval which is finishing first
      if (arr1[i].end < arr2[j].end)
        i++;
      else
        j++;
    }

    return result.toArray(new Interval[result.size()]);
  }

  public static void main(String[] args) {
    Interval[] input1 = new Interval[] { new Interval(1, 3), new Interval(5, 6), new Interval(7, 9) };
    Interval[] input2 = new Interval[] { new Interval(2, 3), new Interval(5, 7) };
    Interval[] result = IntervalsIntersection.merge(input1, input2);
    System.out.print("Intervals Intersection: ");
    for (Interval interval : result)
      System.out.print("[" + interval.start + "," + interval.end + "] ");
    System.out.println();

    input1 = new Interval[] { new Interval(1, 3), new Interval(5, 7), new Interval(9, 12) };
    input2 = new Interval[] { new Interval(5, 10) };
    result = IntervalsIntersection.merge(input1, input2);
    System.out.print("Intervals Intersection: ");
    for (Interval interval : result)
      System.out.print("[" + interval.start + "," + interval.end + "] ");
  }
}

// output:
// Intervals Intersection: [2,3] [5,6] [7,7]
// Intervals Intersection: [5,7] [9,10]

Conflicting Appointments

Write a program to find conflicts in a list of appointments. Let’s say that you are writing a calendar program and you need a method to find conflicting meetings on the schedule.

You have a class

class Appointment {
    long start;
    long end;
    boolean hasConflict = false;
}

The method signature should look like

1	`public void findConflicts(List<Appointment> appts)`

So say that your meetings look something like the following

|------------|
                   |---------------|
                        |----------------|

The first meeting doesn’t conflict with any other meetings. The second and third meeting overlap so in the result set hasConflict will be false for the first appointment and true for the second and third.

Source: Conflicting Appointments

Explanation

Sort the appointments by their start time.
Initialize the first appointment be the latest appointment to compare with the iterated appointment. Loop from the second appointment to the end. If the iterated appointment’s start is less than the latest appointment’s end, then we set both of them be conflict. Also, in each iteration, we update the latest appointment be the appointment that has the latest ending time.

Solution

public void findConflicts(List<Appointment> appts) {
    if (appts == null || appts.size() < 2) return;
    Appointment latest = appts.get(0);
    for (int i = 1; i < appts.size(); i++) {
        if (appts.get(i).start < latest.end) {
            appts.get(i).hasConflict = true;
            latest.hasConflict = true;
        }
        if (appts.get(i).end > latest.end) {
            latest = appts.get(i);
        }
    }
}

Cyclic Sort

Given an array of n unique integers where the range is 1 ≤ a[i] ≤ n (n = size of array). Sort the array using Cyclic Sort.

Explanation

When array numbers in a given range, we can try solve it using Cyclic Sort.
Initiaize a variable idx that is the index to check if the current index’s element is in the right position. The correct position for number nums[idx] is nums[idx]-1. We check by comparing nums[idx] and nums[ nums[idx]-1 ]. If these two numbers are different, we swap them to put nums[idx] in the correct position; else we increase idx to check the next element; repeat this while loop until idx exceed the length of the array.

Solution

void swap(int[] nums, int a, int b) {
    int temp = nums[a];
    nums[a] = nums[b];
    nums[b] = temp;
}

void sort(int[] nums) {
    int idx = 0;

    while (idx < nums.length) {
        if (nums[idx] != nums[nums[idx] - 1]) {
            swap(nums, idx, nums[idx] - 1);
        } else {
            idx += 1;
        }
    }
}

LeetCode 268. Missing Number

Given an array containing n distinct numbers taken from 0, 1, 2, ..., n, find the one that is missing from the array.

Example 1:

Input: [3,0,1]
Output: 2

Example 2:

Input: [9,6,4,2,3,5,7,0,1]
Output: 8

Note:

Your algorithm should run in linear runtime complexity. Could you implement it using only constant extra space complexity?

Explanation

First, we can use Cyclic Sort to put the elements in its correct position, note in this problem, if the current element is equal to n, then we can just ignore it and increase the index idx since its correct position will be outside of the array.
After we sort the array, we can loop from the beginning and compare the element with its index. If they are not equal, then we return the index which is the missing number.
If all elements are equal to its index, the missing number will be n which is the length of the array.

Solution

class Solution {
    void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }

    public int missingNumber(int[] nums) {
        if (nums == null || nums.length == 0) return 0;
        int idx = 0;
        while (idx < nums.length) {
            if (nums[idx] != nums.length && nums[idx] != nums[nums[idx]]) {
                swap(nums, idx, nums[idx]);
            } else {
                idx += 1;
            }
        }

        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i) {
                return i;
            }
        }

        return nums.length;
    }
}

LeetCode 448. Find All Numbers Disappeared in an Array

Given an array of integers where 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.

Find all the elements of [1, n] inclusive that do not appear in this array.

Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.

Example:

Input:
[4,3,2,7,8,2,3,1]

Output:
[5,6]

Explanation

We can use cyclic sort to solve this problem. If the input array is [4,3,2,7,8,2,3,1], after cyclic sort, it becomes [1, 2, 3, 4, 3, 2, 7, 8]. Then, we loop through this array and find the missing number which are 5 and 6.

Solution

class Solution {
    void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }

    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0) return res;
        int idx = 0;

        while (idx < nums.length) {
            if (nums[idx] != nums[nums[idx] - 1]) {
                swap(nums, idx, nums[idx] - 1);
            } else {
                idx += 1;
            }
        }

        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i+1) {
                res.add(i+1);
            }
        }
        return res;
    }
}

LeetCode 287. Find the Duplicate Number

Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.

Example 1:

Input: [1,3,4,2,2]
Output: 2

Example 2:

Input: [3,1,3,4,2]
Output: 3

Note:

You must not modify the array (assume the array is read only).
You must use only constant, O(1) extra space.
Your runtime complexity should be less than O(n^2).
There is only one duplicate number in the array, but it could be repeated more than once.

Explanation 1

If we can modify the array, We can use cyclic sort to solve the array. In this problem, after sorting, the last element will the duplicated number since there are n+1 numbers and all numbers are between 1 to n.

Solution 1

class Solution {
    void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }

    public int findDuplicate(int[] nums) {
        int idx = 0;
        while (idx < nums.length) {
            if (nums[idx] != nums[nums[idx] - 1]) {
                swap(nums, idx, nums[idx]-1);
            } else {
                idx += 1;
            }
        }
        return nums[nums.length - 1];
    }
}

Explanation 2

Without modify the array, this problem can use the same technique as 142. Linked List Cycle II since there are duplicated number in the array and each integer is between 1 and n (inclusive), it must have a cycle. For example, if the input is [1, 2, 3, 4, 2], we have (both the duplicated number 2 are pointing to 3):
1
2
3
1->2->3->4->2 | | <------
Initialize slow and fast be 0, then slow moves one step, slow = nums[slow];fast moves two steps, fast = nums[fast]; fast = nums[fast], in other words, fast = nums[nums[fast]]. Repeat this step, until slow = fast, which is their meeting point.
Then, slow set to 0 instead of nums[0] because in 142. Linked List Cycle II this method, we find the cycle starting point which is 3 in the above example, but now we want to find the point that is one step before the the cycle starting point, so we set slow to 0. Now slow and fast move at the same speed, this time their meeting point is the beginning of the cycle, which is the duplicated number.

Solution 2

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = 0, fast = 0;
        while (true) {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if (slow == fast) break;
        }
        slow = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
}

LeetCode 442. Find All Duplicates in an Array

Given an array of integers, 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.

Find all the elements that appear twice in this array.

Could you do it without extra space and in $O(n)$ runtime?

Example:

Input:
[4,3,2,7,8,2,3,1]

Output:
[2,3]

Explanation

We can use cyclic sort to sort this array. After sorting, loop this array fom index 0 to the end, if the element’s value is not equal to idx + 1, that means the element nums[idx] is duplicated.

Solution

class Solution {
    void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }

    public List<Integer> findDuplicates(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0) return res;
        int idx = 0;

        while (idx < nums.length) {
            if (nums[idx] != nums[nums[idx] - 1]) {
                swap(nums, idx, nums[idx] - 1);
            } else {
                idx += 1;
            }
        }

        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i+1) {
                res.add(nums[i]);
            }
        }

        return res;
    }
}

In-place Reversal of a LinkedList

LeetCode 206. Reverse Linked List

Reverse a singly linked list.

Example:

Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL

Follow up:

A linked list can be reversed either iteratively or recursively. Could you implement both?

Explanation 1

Make an empty ListNode called pre and think of it as the head of the already reversed ListNode, make a cur pointer pointing to head.
While cur is not empty, first store cur.next as a temp linked list called nex, then cur.next = pre which means append cur to the head of the reversed ListNode. Then update pre = cur which means now the pre is the head of the reversed ListNode. Then update cur = nex which means cur is moving forward 1 step. Repeat until cur is NULL,
Return pre.

Solution 1

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) return head;
        ListNode pre = null;
        ListNode cur = head;
        while (cur != null) {
            ListNode nex = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nex;
        }
        return pre;
    }
}

Explanation 2

We can also use recursive method to solve this problem. The newHead will be the last node of the linked list, then the head will be the second last node of the linked list. We make head.next.next = head which means now the last node (newHead)’s next pointing to the second last node and the second last node now is the last node. Then we head.next = null to cut off the new last node. Then we return newHead.

Solution 2

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) return head;
        ListNode newHead = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}

LeetCode 92. Reverse Linked List II

Reverse a linked list from position m to n. Do it in one-pass.

Note: 1 ≤ m ≤ n ≤ length of list.

Example:

Input: 1->2->3->4->5->NULL, m = 2, n = 4
Output: 1->4->3->2->5->NULL

Explanation

First, we need to know mNode and nNode’s correct position.
We need to create one more node that is pointing at the previous of mNode called preM. For example, linked list is 1->2->3->4->5, m = 2 n = 4, so preM points at element 1, mNode points at element 2, nNode points at element 4. Then, we move mNode to the next of nNode, then update mNode to its next element, and repeat this process until mNode and nNode point at the same element. We can illustrate this process below:
1
2
3
1->2->3->4->5 1->3->4->2->5 1->4->3->2->5

Solution

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode reverseBetween(ListNode head, int m, int n) {
        if (head == null || head.next == null) return head;
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        ListNode preM = dummy;
        ListNode mNode = head;
        ListNode nNode = head;
        for (int i = 1; i < m; i++) {
            preM = mNode;
            mNode = mNode.next;
        }
        for (int i = 1; i < n; i++) {
            nNode = nNode.next;
        }

        while (mNode != nNode) {
            preM.next = mNode.next;
            mNode.next = nNode.next;
            nNode.next = mNode;
            mNode = preM.next;
        }

        return dummy.next;
    }
}

LeetCode 25. Reverse Nodes in k-Group

Given a linked list, reverse the nodes of a linked list k at a time and return its modified list.

k is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of k then left-out nodes in the end should remain as it is.

Example:

Given this linked list: 1->2->3->4->5

For k = 2, you should return: 2->1->4->3->5

For k = 3, you should return: 3->2->1->4->5

Note:

Only constant extra memory is allowed.
You may not alter the values in the list’s nodes, only nodes itself may be changed.

Explanation

The last solution use a stack that costs $O(n)$ space. This time, we don’t need extra space. Like the last solution, we need to create a dummy node in front of the input node’s head, and need a pre pointer that points to dummy node, last pointer that points to the $k+1$’s node.
1
2
3
dummy -> 1 -> 2 -> 3 -> 4 -> 5 | | pre last
Now, we need to reverse the nodes between pre (exclusive) and last (exclusive), we can think of this as a sublist.

We should starts from the second node in this sublist, which is node 2. We have a cur pointing to node 2 and make it become the first node. Then, cur pointing to node 3 and make node 3 pointing to the beginning of the node, and we are done reversing. Also, before we start reverse, we should have a tail node that points to 1 because it will eventually be the tail of this sublist. Finally, when cur equals to last, we are done. Before we checking the next $k$ nodes, we need to set the pre to tail and start moving the last $k$ steps next.

           dummy -> 1 -> 2 -> 3 -> 4 -> 5
               |    |    |         |
             pre   tail  cur      last

           dummy -> 2 -> 1 -> 3 -> 4 -> 5
               |         |    |    |
             pre        tail cur  last

           dummy -> 3 -> 2 -> 1 -> 4 -> 5
               |              |    |
             pre             tail (cur)last

For example, in the above second step, we want to move 2 in front of 1, we can set the nex pointer pointing to 3, then do the following:

           dummy -> 1 -> 2 -> 3 -> 4 -> 5
               |    |    |    |    |
             pre   tail  cur  nex  last

           cur.next = pre.next
           2 -> 1 -> 2 -> 3 -> 4 -> 5

           pre.next = cur
           dummy -> 2 -> 1 -> 2 -> 3 -> 4 -> 5

           tail.next = nex
           dummy -> 2 -> 1 -> 3 -> 4 -> 5

Solution

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    ListNode reverseKNode(ListNode pre, int k) {
        ListNode last = pre;
        for (int i = 0; i < k+1; i++) {
            last = last.next;
            if (last == null && i != k) return null;
        }
        ListNode tail = pre.next;
        ListNode cur = pre.next.next;
        while (cur != last) {
            ListNode nex = cur.next;
            cur.next = pre.next;
            pre.next = cur;
            tail.next = nex;
            cur = nex;
        }
        return tail;
    }

    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        ListNode pre = dummy;
        while (pre != null) {
            pre = reverseKNode(pre, k);
        }
        return dummy.next;
    }
}

Tree Breadth First Search

LeetCode 102. Binary Tree Level Order Traversal

Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level).

For example: Given binary tree [3,9,20,null,null,15,7],

return its level order traversal as:

[
  [3],
  [9,20],
  [15,7]
]

Explanation

We can use the BFS method. We store each layer’s values into a list, then add this list into the result. The problem now of the BFS is we don’t know the number of elements in each layer. To solve this, we need to record the size of each layer before we pop and push the left child and right child elements into the list, and we pop the number of elements base on this size.
From the above example, we first push 3 into the queue, record the size is 1, then we pop 1 element adding to a list, then push its left and right child 9 and 20, now the queue has 2 elements, so we update the size to 2. Then we should pop 2 elements this time, we pop 9, pop 20, adding to a list, and push its left and right child 15 and 7. Now the queue has 2 elements, so we update its size to 2, and we only pop size=2 elements and adding to the list, etc, until the queue is empty.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            List<Integer> sub = new ArrayList<>();
            for (int i = queue.size() - 1; i >= 0; i--) {
                TreeNode popNode = queue.poll();
                sub.add(popNode.val);
                if (popNode.left != null) queue.offer(popNode.left);
                if (popNode.right != null) queue.offer(popNode.right);
            }
            res.add(sub);
        }

        return res;
    }
}

LeetCode 107. Binary Tree Level Order Traversal II

Given a binary tree, return the bottom-up level order traversal of its nodes’ values. (ie, from left to right, level by level from leaf to root).

For example: Given binary tree [3,9,20,null,null,15,7],

return its bottom-up level order traversal as:

[
  [15,7],
  [9,20],
  [3]
]

Explanation

Same as Binary Tree Level Order Traversal, but this time when we add the sub-list to the result list, we add the sublist in front of the result list.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            List<Integer> sub = new ArrayList<>();
            for (int i = queue.size() - 1; i >= 0; i--) {
                TreeNode popNode = queue.poll();
                sub.add(popNode.val);
                if (popNode.left != null) queue.add(popNode.left);
                if (popNode.right != null) queue.add(popNode.right);
            }
            res.add(0, sub);
        }
        return res;
    }
}

LeetCode 103. Binary Tree Zigzag Level Order Traversal

Given a binary tree, return the zigzag level order traversal of its nodes’ values. (ie, from left to right, then right to left for the next level and alternate between).

For example: Given binary tree [3,9,20,null,null,15,7],

return its zigzag level order traversal as:

[
  [3],
  [20,9],
  [15,7]
]

Explanation

Similar to 102. Binary Tree Level Order Traversal, but this time we need to add value from left to right, in the next level, we add values from right to left. Then next level, add values from left to right, next level from right to left.
When the current level is from left to right, we can normally pop value from the beginning and add its child to the end (left child first). When the current level is from right to left, we pop values from the end and add its child (right child first) to the beginning.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if (root == null) return res;
        LinkedList<TreeNode> queue = new LinkedList<>();
        boolean leftToRight = true;
        queue.add(root);
        while (!queue.isEmpty()) {
            int size = queue.size();
            List<Integer> lst = new ArrayList<>();
            if (leftToRight) {
                for (int i = 0; i < size; i++) {
                    TreeNode temp = queue.remove(0);
                    lst.add(temp.val);
                    if (temp.left != null) queue.add(temp.left);
                    if (temp.right != null) queue.add(temp.right);
                }
            } else {
                for (int i = 0; i < size; i++) {
                    TreeNode temp = queue.remove(queue.size()-1);
                    lst.add(temp.val);
                    if (temp.right != null) queue.add(0, temp.right);
                    if (temp.left != null) queue.add(0, temp.left);
                }
            }
            res.add(lst);
            leftToRight = !leftToRight;
        }

        return res;
    }
}

LeetCode 637. Average of Levels in Binary Tree

Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array.

Example 1:

Input:
    3
   / \
  9  20
    /  \
   15   7
Output: [3, 14.5, 11]
Explanation:
The average value of nodes on level 0 is 3,  on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].

Note:

The range of node’s value is in the range of 32-bit signed integer.

Explanation

We can solve this problem using level-order traversal, in other words, BFS. For each level, we use a variable sum to sum all the numbers on the same level. After we finish iterating all numbers on the same level, we then calculate the average by sum divide the numbers of that level.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> res = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            double sum = 0;
            int n = queue.size();
            for (int i = n-1; i >= 0; i--) {
                TreeNode popNode = queue.poll();
                sum += popNode.val;
                if (popNode.left != null) queue.offer(popNode.left);
                if (popNode.right != null) queue.offer(popNode.right);
            }
            res.add(sum / n);
        }
        return res;
    }
}

111. Minimum Depth of Binary Tree

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

return its minimum depth = 2.

Explanation

If the leaf node is next to the root node, then we can stop there. In other words, if the popNode doesn’t have left and right nodes, we can return this level’s depth. We can use level-order traversal to solve this problem.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        int res = 0;
        if (root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            for (int i = queue.size()-1; i >= 0; i--) {
                TreeNode popNode = queue.poll();
                if (popNode.left == null && popNode.right == null) return res + 1;
                if (popNode.left != null) queue.offer(popNode.left);
                if (popNode.right != null) queue.offer(popNode.right);
            }
            res += 1;
        }
        return res;
    }
}

Level Order Successor

Given a binary tree and a node in the binary tree, find Levelorder successor of the given node. That is, the node that appears after the given node in the level order traversal of the tree.

Note: The task is not just to print the data of the node, you have to return the complete node from the tree.

Examples:

Consider the following binary tree
              20
           /      \
          10       26
         /  \     /   \
       4     18  24    27
            /  \
           14   19
          /  \
         13  15

Levelorder traversal of given tree is:
20, 10, 26, 4, 18, 24, 27, 14, 19, 13, 15

Input : 24
Output : 27

Input : 4
Output : 18

Source: Level Order Successor of a node in Binary Tree

Explanation

First we check if the root node is the given node. If true, then we return its left node, if there’s no left node, we return its right node; if there’s also no right node, we return NULL.
If the root node is not the given node, we do level-order traversal. When the pollNode is the given node, we break out the while loop and return the first node of the queue.

Solution

Node solve(Node root, Node key) {
    if (root == null) return null;

    if (root == key) {
        if (root.left != null) return root.left;
        else if (root.right != null) return root.right;
        else return null;
    }

    Queue<Node> queue = new LinkedList<Node>();
    queue.offer(root);

    while (!queue.isEmpty()) {
        Node pollNode = queue.poll();
        if (pollNode.left != null) queue.add(pollNode.left);
        if (pollNode.right != null) queue.add(pollNode.right);
        if (pollNode == key) break;
    }

    return queue.peek();
}

LeetCode 117. Populating Next Right Pointers in Each Node II

Given a binary tree

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

You may only use constant extra space.
Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Constraints:

The number of nodes in the given tree is less than 6000.
-100 <= node.val <= 100

Explanation 1

We can use level-order traversal to solve this problem. Initially, we push the root node to the queue, then we also push the NULL node to the queue to mark it as the end of the current level. While the queue is not empty, we loop queue.size() - 1 times since the queue size will be 2 at the beginning, but 1 of the node is just the NULL node.
In each iteration, we poll a node from the queue. Then assign pollNode.next to be queue.peek() since the first node of inside the queue will always be the next node of the pollNode. After looping all nodes from the current level, in other words, after looping queue.size() - 1 times, we poll the NULL node out from the queue and push the NULL node to the end of the queue.

Solution 1

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/
class Solution {
    public Node connect(Node root) {
        if (root == null) return root;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        queue.offer(null);
        while (queue.peek() != null) {
            for (int i = queue.size()-1; i > 0; i--) {
                Node pollNode = queue.poll();
                pollNode.next = queue.peek();
                if (pollNode.left != null) queue.offer(pollNode.left);
                if (pollNode.right != null) queue.offer(pollNode.right);
            }
            queue.poll();
            queue.offer(null);
        }
        return root;
    }
}

Explanation 2

This solution uses O(1) space and it is iterating level by level.
First, we create a dummy node that is used to pointing before the first element of each level. We create a pointer cur = dummy that is used to iterate the current level’s element.
Then, if the left subnode exists, cur.next connects it, then iterate cur = cur.next. If the right subnode exists, cur.next connects it, then iterate cur = cur.next. Now, the root’s left and right subnodes are connected.
Then, we move curRoot to the right. After we move, if curRoot is not exist, then it means we finish connecting to current root node’s sub node. We then reset curRoot to dummy’s next node.
We cut off dummy.next = null, and cur reset pointing to dummy. We set dummy’s next to null because we want the cur pointer’s next to NULL so that we can use cur.next to point to the first element in the next level.

Solution 2

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/
class Solution {
    public Node connect(Node root) {
        if (root == null) return root;
        Node dummy = new Node(-1);
        Node cur = dummy;
        Node curRoot = root;
        while (curRoot != null) {
            if (curRoot.left != null) {
                cur.next = curRoot.left;
                cur = cur.next;
            }
            if (curRoot.right != null) {
                cur.next = curRoot.right;
                cur = cur.next;
            }
            if (curRoot.next != null) {
                curRoot = curRoot.next;
            } else {
                curRoot = dummy.next;
                dummy.next = null;
                cur = dummy;
            }
        }
        return root;
    }
}

Tree Depth First Search

LeetCode 112. Path Sum

Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \      \
7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

Explanation

We can use recursion to solve this problem. In the recrsive method, we pass the root and sum as parameters. If the root is null, then we return false. If the root has not left and no right child and its value is equals to the sum, then we return true. Then, we can recursively call this method for the left subtree and right subtree.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) return false;
        if (sum == root.val && root.left == null && root.right == null) return true;
        return hasPathSum(root.left, sum-root.val) || hasPathSum(root.right, sum-root.val);
    }
}

LeetCode 113. Path Sum II

Given a binary tree and a sum, find all root-to-leaf paths where each path’s sum equals the given sum.

Note: A leaf is a node with no children.

Example:

Given the below binary tree and sum = 22,

      5
     / \
    4   8
   /   / \
  11  13  4
 /  \    / \
7    2  5   1

Return:

[
   [5,4,11,2],
   [5,8,4,5]
]

Explanation

We can use recusive backtracking to solve this, so we create a helper function and pass a temp list and result list as the parameters besides the root node and sum.
Inside the helper function, the base case is if the root node is NULL, we just return nothing. Then, we add the current root node’s value to the temp list.
Then we check if the current node’s value equal to the sum and also there’s no left and right node, then we add temp list to the result list.
Next, we recrusively call the helper function with the left and right child nodes with the updated sum=sum-root.val. Then, we should remove the last element of the temp list in order to backtract to the parent node.

Solution

class Solution {
    void helper(TreeNode root, int sum, List<List<Integer>> res, List<Integer> cur) {
        if (root == null) return;
        cur.add(root.val);
        if (root.val == sum && root.left == null && root.right == null) {
            res.add(new ArrayList<>(cur));
        }
        helper(root.left, sum-root.val, res, cur);
        helper(root.right, sum-root.val, res, cur);
        cur.remove(cur.size()-1);
    }

    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        helper(root, sum, res, new ArrayList<>());
        return res;
    }
}

LeetCode 129. Sum Root to Leaf Numbers

Given a binary tree containing digits from 0-9 only, each root-to-leaf path could represent a number.

An example is the root-to-leaf path 1->2->3 which represents the number 123.

Find the total sum of all root-to-leaf numbers.

Note: A leaf is a node with no children.

Example:

Input: [1,2,3]
    1
   / \
  2   3
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

Input: [4,9,0,5,1]
    4
   / \
  9   0
 / \
5   1
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Explanation

We can use recursive DFS to solve this problem. First, we create a sum variable to hold the path sum, and since we are using recursion, in order to make sure the sum is the latest updated sum, we allocate a memory space, so we use an array that has size 1 to save the sum.
In the helper function, we pass the root, sum, and also the current sum, which is 0 initially. Inside the helper function, the base case is if the root is NULL, we just return nothing. Next, we update the curSum = curSum * 10 + root.val. Now, we check if the current TreeNode is the leaf, if it’s a leaf node, then we add curSum to sum. Next, we recursively check the left and right child node. After checking the left and right child node, we need to backtrack the curSum /= 10 to remove the the current node’s value from curSum.

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    void helper(TreeNode root, int[] sum, int curSum) {
        if (root == null) return;
        curSum = curSum * 10 + root.val;
        if (root.left == null && root.right == null) {
            sum[0] += curSum;
        }
        helper(root.left, sum, curSum);
        helper(root.right, sum, curSum);
        curSum /= 10;
    }

    public int sumNumbers(TreeNode root) {
        int[] sum = new int[]{0};
        if (root == null) return sum[0];
        helper(root, sum, 0);
        return sum[0];
    }
}

Path With Given Sequence

Given a binary tree and an array, the task is to find if the given array sequence is present as a root to leaf path in given tree.

Examples :

    5
   / \
  2   3
 / \
1   4
   / \
  6   8

Input : arr[] = {5, 2, 4, 8} for above tree
Output: true

Input :  arr[] = {5, 3, 4, 9} for above tree
Output: false

Source: Check if there is a root to leaf path with given sequence

Explanation

We can use pre-order traversal to traverse the tree. We will pass the root node, the array, and also the current index which initialize to 0 into the helper function.
Inside the helper function, we first check if the current root node is valid. Then the base case is if the current root node is not equal to the current element of the array, we return false; or the current index is greater than the size of the array, we also return false.
If the current node is leaf node and its value is equal to the current element and also the last element of the array, we return true.
Else the root node’s value is equal to the current element of the array, but it’s not the leaf node, we will recursively calling the helper function with the left child and index plus 1, and calling the helper function with the right child and index plus 1.

Solution

boolean helper(Node root, int[] arr, int idx) {
    if (root == null) return false;
    if (idx >= arr.length || root.val != arr[idx]) return false;
    if (root.left == null && root.right == null && idx == arr.length - 1) return true;
    return helper(root.left, arr, idx+1) || helper(root.right, arr, idx+1);
}

boolean solve(Node root, int[] arr) {
    if (arr == null) return root == null;
    return helper(root, sequence, 0)
}

LeetCode 437. Path Sum III

You are given a binary tree in which each node contains an integer value.

Find the number of paths that sum to a given value.

The path does not need to start or end at the root or a leaf, but it must go downwards (traveling only from parent nodes to child nodes).

The tree has no more than 1,000 nodes and the values are in the range -1,000,000 to 1,000,000.

Example:

root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

Return 3. The paths that sum to 8 are:

1.  5 -> 3
2.  5 -> 2 -> 1
3. -3 -> 11

Explanation

We can use DFS to solve this problem. In the helper function, we will pass the root, sum, and also the result variable res[0] = {0} as parameters.
Inside the helper function, the base case is if the root is NULL, we just return nothing. If the root’s value is equal to the sum, then we increase res.
Next, we will recursively call the helper function with left, right child node with updated sum = sum - root.val.
Under the main function, we should also consider that the left child as root, and right child as root, so we return res plus the result of pathSum(root.left, sum) and pathSum(root.right, sum).

Solution

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    void helper(TreeNode root, int sum, int[] res) {
        if (root == null) return;
        if (root.val == sum) res[0] += 1;
        helper(root.left, sum-root.val, res);
        helper(root.right, sum-root.val, res);
    }

    public int pathSum(TreeNode root, int sum) {
        int[] res = new int[]{0};
        if (root == null) return res[0];
        helper(root, sum, res);
        return res[0] + pathSum(root.left, sum) + pathSum(root.right, sum);
    }
}

Two Heaps

LeetCode 295. Find Median from Data Stream

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

For example,

[2,3,4], the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

void addNum(int num) - Add a integer number from the data stream to the data structure.
double findMedian() - Return the median of all elements so far.

Example:

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3)
findMedian() -> 2

Follow up:

If all integer numbers from the stream are between 0 and 100, how would you optimize it?
If 99% of all integer numbers from the stream are between 0 and 100, how would you optimize it?

Explanation

Initialize a minHeap and maxHeap to each store half of the numbers. If the number we are adding are 6, 8, 10, 7, 9, 11, 13, 12. Then, maxHeap stores the number are 10, 9, 8, 7, 6; minHeap stores the number will be 11, 12, 13, 14, 15. To find the median, if these two heaps has the same length, we can just sum both peek heap’s number and divide by 2, in other words, (10+11)/2.0. When adding number, we store to the minHeap first, if these two heap’s size is different, we can just peek the minHeap’s number as the result.
When adding number, we store it to minHeap first, then we pop out minHeap’s number and store it to maxHeap. If maxHeap’s size is greater than minHeap, we will pop maxHeap’s element back to minHeap. This ensures that elements in the minHeap are greater than maxHeap. So maxHeap stores the number are 10, 9, 8, 7, 6; minHeap stores the number will be 11, 12, 13, 14, 15.

Solution

class MedianFinder {

    /** initialize your data structure here. */
    Queue<Integer> minHeap;
    Queue<Integer> maxHeap;

    public MedianFinder() {
        minHeap = new PriorityQueue<>();
        maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
    }

    public void addNum(int num) {
        minHeap.offer(num);
        maxHeap.offer(minHeap.poll());
        if (maxHeap.size() > minHeap.size()) {
            minHeap.offer(maxHeap.poll());
        }
    }

    public double findMedian() {
        if (minHeap.size() == maxHeap.size()) {
            return (maxHeap.peek() + minHeap.peek()) / 2.0;
        } else {
            return (double) minHeap.peek();
        }
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */

LeetCode 480. Sliding Window Median

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Examples:

[2,3,4] , the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Your job is to output the median array for each window in the original array.

For example,

Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.

Window position                Median
---------------               -----
[1  3  -1] -3  5  3  6  7       1
 1 [3  -1  -3] 5  3  6  7       -1
 1  3 [-1  -3  5] 3  6  7       -1
 1  3  -1 [-3  5  3] 6  7       3
 1  3  -1  -3 [5  3  6] 7       5
 1  3  -1  -3  5 [3  6  7]      6

Therefore, return the median sliding window as [1,-1,-1,3,5,6].

Note:

You may assume k is always valid, ie: k is always smaller than input array’s size for non-empty array.

Explanation

To find a median number, we can use two heaps to split the window elements. One is maxHeap to store the numbers that are less than the median, another one is minHeap to store the numbers that are equal or only one more than the size of maxHeap.

For example, if the input nums = [5, 6, 7, 8, 9], and window length k = 3.

 maxHeap: []; minHeap: [5]
 maxHeap: [5]; minHeap: [6]
 maxHeap: [5]; minHeap: [6, 7]
 maxHeap: [6, 5]; minHeap: [7, 8]
 maxHeap: [6, 5]; minHeap: [7, 8, 9]

We create a getMedian function. In this function, if both heaps are empty, then we return 0 as the median result. Else if their heap size is different, in other words, the minHeap has size one more than the maxHeap, we will peek the minHeap as the median element. Else if both heap has the same size, then we peek both heaps and divide the sum of both peek element by 2 as the median.
When we iterate the input element, how do we know which heap we are going to add into. We can compare the current element with the result of getMedian. If the current element is greater than the median value, we add into minHeap, else maxHeap. Then we balance both heaps.
When the window length is equals to k we need to remove the most left side element of the window from either minHeap or maxHeap. So if this element is less than the median result of the getMedian function, we remove from the maxHeap, else the minHeap. Then, we need to balance both heaps.
Note, when we create the maxHeap, the comparator function should be (a, b) -> b.compareTo(a), not (a, b) -> b - a because the input elements can be all negative.

Solution

class Solution {
    PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
    PriorityQueue<Integer> minHeap = new PriorityQueue<>();

    void addNum(int num) {
        minHeap.offer(num);
        maxHeap.offer(minHeap.poll());
        if (maxHeap.size() > minHeap.size()) {
            minHeap.offer(maxHeap.poll());
        }
    }

    double getMedian() {
        if (maxHeap.size() == minHeap.size()) {
            return ((double)maxHeap.peek() + (double)minHeap.peek()) / 2.0;
        } else {
            return minHeap.peek();
        }
    }

    void removeNum(int num) {
        double median = getMedian();
        if (num < median) {
            maxHeap.remove(num);
        } else {
            minHeap.remove(num);
        }
        if (maxHeap.size() + 1 < minHeap.size()) {
            maxHeap.offer(minHeap.poll());
        } else if (minHeap.size() < maxHeap.size()) {
            minHeap.offer(maxHeap.poll());
        }
    }

    public double[] medianSlidingWindow(int[] nums, int k) {
        double[] res = new double[nums.length-k+1];
        for (int i = 0; i < nums.length; i++) {
            addNum(nums[i]);
            if (i+1 >= k) {
                res[i+1-k] = getMedian();
                removeNum(nums[i+1-k]);
            }
        }
        return res;
    }
}

LeetCode 502. IPO

Suppose LeetCode will start its IPO soon. In order to sell a good price of its shares to Venture Capital, LeetCode would like to work on some projects to increase its capital before the IPO. Since it has limited resources, it can only finish at most k distinct projects before the IPO. Help LeetCode design the best way to maximize its total capital after finishing at most k distinct projects.

You are given several projects. For each project i, it has a pure profit Pi and a minimum capital of Ci is needed to start the corresponding project. Initially, you have W capital. When you finish a project, you will obtain its pure profit and the profit will be added to your total capital.

To sum up, pick a list of at most k distinct projects from given projects to maximize your final capital, and output your final maximized capital.

Example 1:

Input: k=2, W=0, Profits=[1,2,3], Capital=[0,1,1].

Output: 4

Explanation: Since your initial capital is 0, you can only start the project indexed 0.
             After finishing it you will obtain profit 1 and your capital becomes 1.
             With capital 1, you can either start the project indexed 1 or the project indexed 2.
             Since you can choose at most 2 projects, you need to finish the project indexed 2 to get the maximum capital.
             Therefore, output the final maximized capital, which is 0 + 1 + 3 = 4.

Note:

You may assume all numbers in the input are non-negative integers.
The length of Profits array and Capital array will not exceed 50,000.
The answer is guaranteed to fit in a 32-bit signed integer.

Explanation

First, we create two heaps. One heap is maxProfit<Integer> which is for storing all profits that we are able to purchase, in other words, their corresponding capital is less than or equal to W; and it sorts by max profit in front. Another heap is capitalProfit<[capital, profit]>, which is for storing pair of capital and profit that we are not able to purchase, in other words, their corresponding capital is greater than W; and it sorts by small capital in front.
First looping over all capital, and update the two heaps we created. Then we loop k times, in each iteration, we update W by poll the first profit from maxProfit. Then, while W is greater than or equal to the first pair’s capital of capitalProfit, we poll this pair out, and push its profit into maxProfit, until W is smaller than the first pair of capitalProfit. Repeat this for loop.

Solution

class Solution {
    public int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {
        PriorityQueue<Integer> maxProfit = new PriorityQueue<>(Comparator.reverseOrder());
        PriorityQueue<int[]> capitalProfit = new PriorityQueue<>((int[] a, int[] b) -> a[0] - b[0]);

        for (int i = 0; i < Capital.length; i++) {
            if (Capital[i] <= W) {
                maxProfit.offer(Profits[i]);
            } else {
                capitalProfit.offer(new int[] {Capital[i], Profits[i]});
            }
        }

        for (int i = 0; i < k; i++) {
            if (maxProfit.isEmpty()) {
                break;
            }
            W += maxProfit.poll();
            while (!capitalProfit.isEmpty() && W >= capitalProfit.peek()[0]) {
                maxProfit.offer(capitalProfit.poll()[1]);
            }
        }

        return W;
    }
}

Subsets

Given a set with distinct elements, find all of its distinct subsets.

Example 1:

Input: [1, 3]
Output: [], [1], [3], [1,3]

Example 2:

Input: [1, 5, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3]

Explanation

To generate all subsets of the given set, we can use the Breadth First Search (BFS) approach. We can start with an empty set, iterate through all numbers one-by-one, and add them to existing sets to create new subsets.

Let’s take the example-2 mentioned above to go through each step of our algorithm:

Given set: [1, 5, 3]

Start with an empty set: [[]]
Add the first number (1) to all the existing subsets to create new subsets: [[], [1]];
Add the second number (5) to all the existing subsets: [[], [1], [5], [1,5]];
Add the third number (3) to all the existing subsets: [[], [1], [5], [1,5], [3], [1,3], [5,3], [1,5,3]].

Here is the visual representation of the above steps:

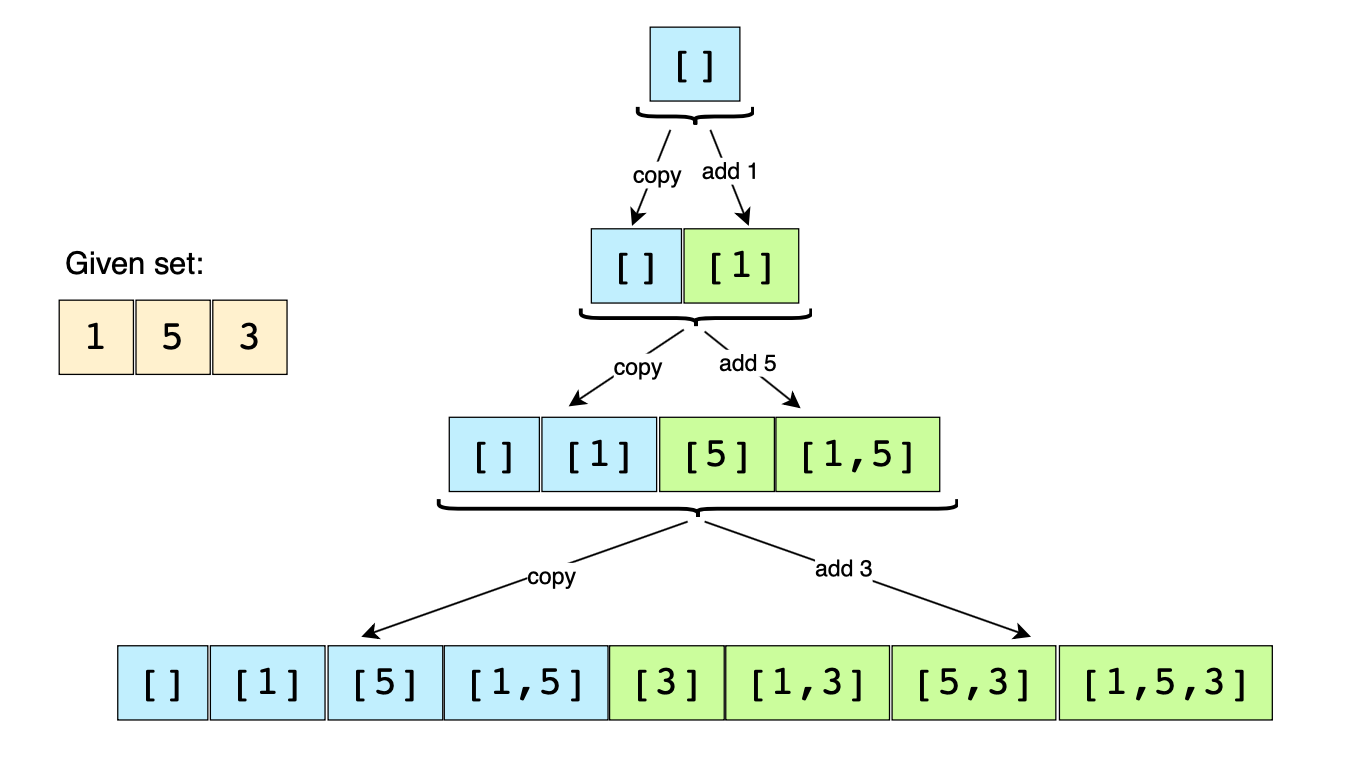
Since the input set has distinct elements, the above steps will ensure that we will not have any duplicate subsets.

Solution

import java.util.*;

class Subsets {

  public static List<List<Integer>> findSubsets(int[] nums) {
    List<List<Integer>> subsets = new ArrayList<>();
    // start by adding the empty subset
    subsets.add(new ArrayList<>());
    for (int currentNumber : nums) {
      // we will take all existing subsets and insert the current number in them to create new subsets
      int n = subsets.size();
      for (int i = 0; i < n; i++) {
        // create a new subset from the existing subset and insert the current element to it
        List<Integer> set = new ArrayList<>(subsets.get(i));
        set.add(currentNumber);
        subsets.add(set);
      }
    }
    return subsets;
  }

  public static void main(String[] args) {
    List<List<Integer>> result = Subsets.findSubsets(new int[] { 1, 3 });
    System.out.println("Here is the list of subsets: " + result);

    result = Subsets.findSubsets(new int[] { 1, 5, 3 });
    System.out.println("Here is the list of subsets: " + result);
  }
}

// output:
// Here is the list of subsets: [[], [1], [3], [1, 3]]
// Here is the list of subsets: [[], [1], [5], [1, 5], [3], [1, 3], [5, 3], [1, 5, 3]]

Source: Subsets

Subsets With Duplicates

Given a set of numbers that might contain duplicates, find all of its distinct subsets.

Example 1:

Input: [1, 3, 3]
Output: [], [1], [3], [1,3], [3,3], [1,3,3]

Example 2:

Input: [1, 5, 3, 3]
Output: [], [1], [5], [3], [1,5], [1,3], [5,3], [1,5,3], [3,3], [1,3,3], [3,3,5], [1,5,3,3]

Explanation

This problem follows the Subsets pattern and we can follow a similar Breadth First Search (BFS) approach. The only additional thing we need to do is handle duplicates. Since the given set can have duplicate numbers, if we follow the same approach discussed in Subsets, we will end up with duplicate subsets, which is not acceptable. To handle this, we will do two extra things:

Sort all numbers of the given set. This will ensure that all duplicate numbers are next to each other.
Follow the same BFS approach but whenever we are about to process a duplicate (i.e., when the current and the previous numbers are same), instead of adding the current number (which is a duplicate) to all the existing subsets, only add it to the subsets which were created in the previous step.

Let’s take Example-2 mentioned above to go through each step of our algorithm:

Given set: [1, 5, 3, 3]
Sorted set: [1, 3, 3, 5]

Start with an empty set: [[]]
Add the first number (1) to all the existing subsets to create new subsets: [[], [1]];
Add the second number (3) to all the existing subsets: [[], [1], [3], [1,3]].
The next number (3) is a duplicate. If we add it to all existing subsets we will get:
1
[[], [1], [3], [1,3], [3], [1,3], [3,3], [1,3,3]]
1
2
We got two duplicate subsets: [3], [1,3] Whereas we only needed the new subsets: [3,3], [1,3,3]
To handle this instead of adding (3) to all the existing subsets, we only add it to the new subsets which were created in the previous (3rd) step:
1
[[], [1], [3], [1,3], [3,3], [1,3,3]]
Finally, add the forth number (5) to all the existing subsets: [[], [1], [3], [1,3], [3,3], [1,3,3], [5], [1,5], [3,5], [1,3,5], [3,3,5], [1,3,3,5]]

Here is the visual representation of the above steps:

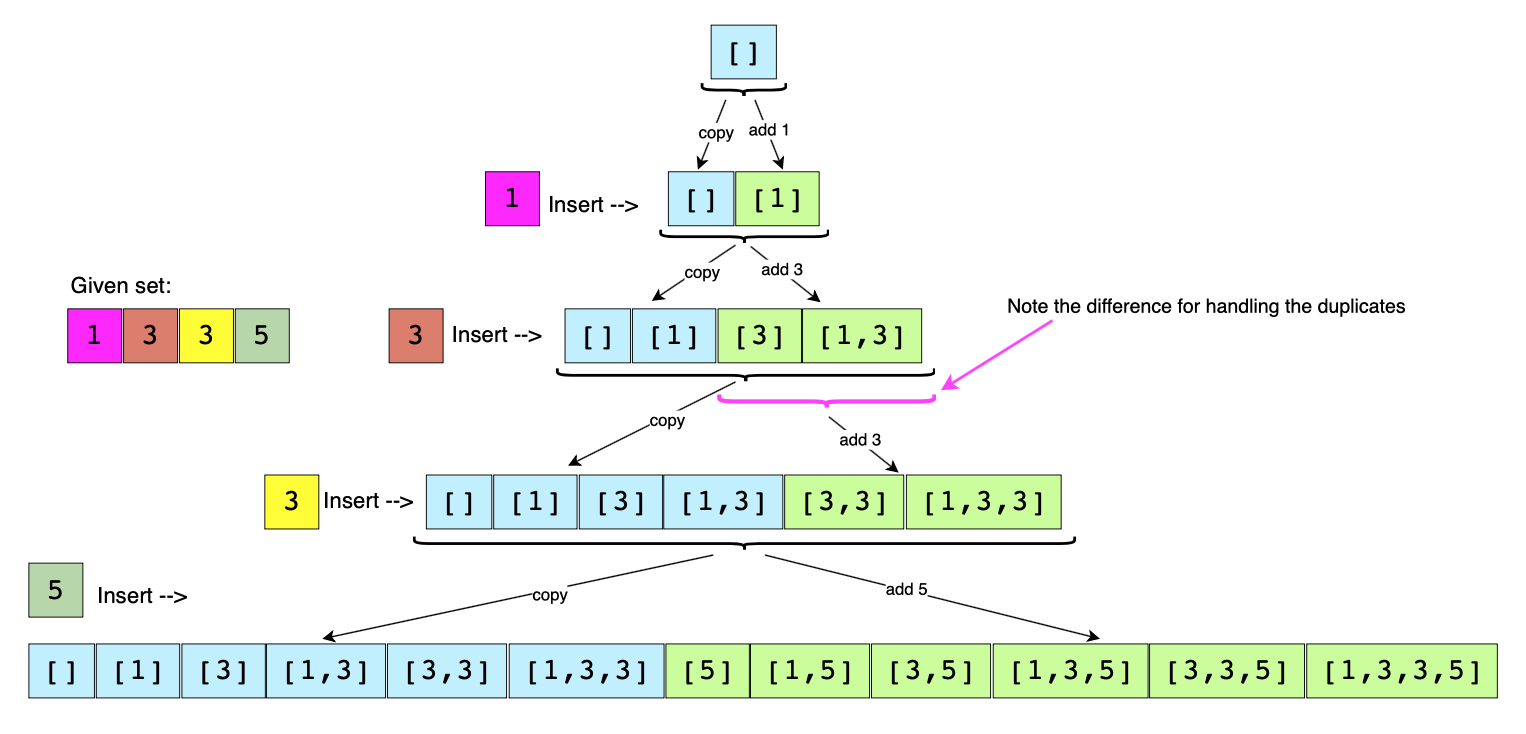
Solution

import java.util.*;

class SubsetWithDuplicates {

  public static List<List<Integer>> findSubsets(int[] nums) {
    // sort the numbers to handle duplicates
    Arrays.sort(nums);
    List<List<Integer>> subsets = new ArrayList<>();
    subsets.add(new ArrayList<>());
    int startIndex = 0, endIndex = 0;
    for (int i = 0; i < nums.length; i++) {
      startIndex = 0;
      // if current and the previous elements are same, create new subsets only from the subsets
      // added in the previous step
      if (i > 0 && nums[i] == nums[i - 1])
        startIndex = endIndex + 1;
      endIndex = subsets.size() - 1;
      for (int j = startIndex; j <= endIndex; j++) {
        // create a new subset from the existing subset and add the current element to it
        List<Integer> set = new ArrayList<>(subsets.get(j));
        set.add(nums[i]);
        subsets.add(set);
      }
    }
    return subsets;
  }

  public static void main(String[] args) {
    List<List<Integer>> result = SubsetWithDuplicates.findSubsets(new int[] { 1, 3, 3 });
    System.out.println("Here is the list of subsets: " + result);

    result = SubsetWithDuplicates.findSubsets(new int[] { 1, 5, 3, 3 });
    System.out.println("Here is the list of subsets: " + result);
  }
}

// Output:
// Here is the list of subsets: [[], [1], [3], [1, 3], [3, 3], [1, 3, 3]]
// Here is the list of subsets: [[], [1], [3], [1, 3], [3, 3], [1, 3, 3], [5], [1, 5], [3, 5], [1, 3, 5], [3, 3, 5], [1, 3, 3, 5]]

Time Complexity

Since, in each step, the number of subsets could double (if not duplicate) as we add each element to all the existing subsets, the time complexity of the above algorithm is $O(2^N)$, where N is the total number of elements in the input set. This also means that, in the end, we will have a total of $O(2^N)$, subsets at the most.

Space Complexity

All the additional space used by our algorithm is for the output list. Since at most we will have a total of $O(2^N)$, subsets, the space complexity of our algorithm is also $O(2^N)$.

Source: Subsets With Duplicates

Permutations

Given a set of distinct numbers, find all of its permutations.

Permutation is defined as the re-arranging of the elements of the set. For example, {1, 2, 3} has the following six permutations:

{1, 2, 3}
{1, 3, 2}
{2, 1, 3}
{2, 3, 1}
{3, 1, 2}
{3, 2, 1}

If a set has n distinct elements it will have $n!$ permutations.

Example 1:

Input: [1,3,5]
Output: [1,3,5], [1,5,3], [3,1,5], [3,5,1], [5,1,3], [5,3,1]

Explanation

This problem follows the Subsets pattern and we can follow a similar Breadth First Search (BFS) approach. However, unlike Subsets, every permutation must contain all the numbers.

Let’s take the example-1 mentioned above to generate all the permutations. Following a BFS approach, we will consider one number at a time:

If the given set is empty then we have only an empty permutation set: []
Let’s add the first element (1), the permutations will be: [1]
Let’s add the second element (3), the permutations will be: [3,1], [1,3]
Let’s add the third element (5), the permutations will be: [5,3,1], [3,5,1], [3,1,5], [5,1,3], [1,5,3], [1,3,5]

Let’s analyze the permutations in the 3rd and 4th step. How can we generate permutations in the 4th step from the permutations of the 3rd step?

If we look closely, we will realize that when we add a new number (5), we take each permutation of the previous step and insert the new number in every position to generate the new permutations. For example, inserting ‘5’ in different positions of [3,1] will give us the following permutations:

Inserting ‘5’ before ‘3’: [5,3,1]
Inserting ‘5’ between ‘3’ and ‘1’: [3,5,1]
Inserting ‘5’ after ‘1’: [3,1,5]

Here is the visual representation of this algorithm:

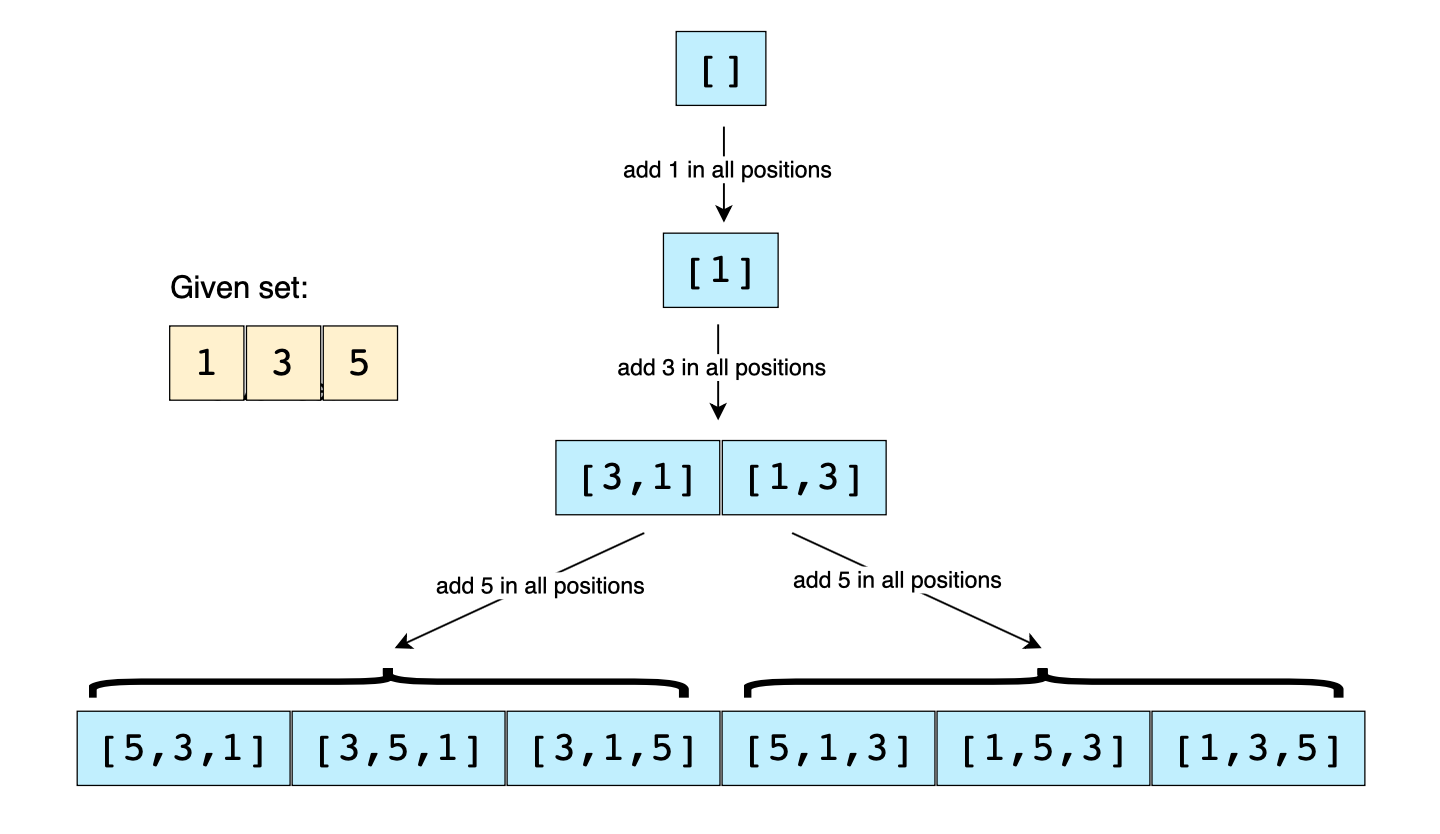
Solution

import java.util.*;

class Permutations {

  public static List<List<Integer>> findPermutations(int[] nums) {
    List<List<Integer>> result = new ArrayList<>();
    Queue<List<Integer>> permutations = new LinkedList<>();
    permutations.add(new ArrayList<>());
    for (int currentNumber : nums) {
      // we will take all existing permutations and add the current number to create new permutations
      int n = permutations.size();
      for (int i = 0; i < n; i++) {
        List<Integer> oldPermutation = permutations.poll();
        // create a new permutation by adding the current number at every position
        for (int j = 0; j <= oldPermutation.size(); j++) {
          List<Integer> newPermutation = new ArrayList<Integer>(oldPermutation);
          newPermutation.add(j, currentNumber);
          if (newPermutation.size() == nums.length)
            result.add(newPermutation);
          else
            permutations.add(newPermutation);
        }
      }
    }
    return result;
  }

  public static void main(String[] args) {
    List<List<Integer>> result = Permutations.findPermutations(new int[] { 1, 3, 5 });
    System.out.print("Here are all the permutations: " + result);
  }
}

// Output:
// Here are all the permutations: [[5, 3, 1], [3, 5, 1], [3, 1, 5], [5, 1, 3], [1, 5, 3], [1, 3, 5]]

Recursive Solution

import java.util.*;

class PermutationsRecursive {

  public static List<List<Integer>> generatePermutations(int[] nums) {
    List<List<Integer>> result = new ArrayList<>();
    generatePermutationsRecursive(nums, 0, new ArrayList<Integer>(), result);
    return result;
  }

  private static void generatePermutationsRecursive(int[] nums, int index, List<Integer> currentPermutation,
      List<List<Integer>> result) {
    if (index == nums.length) {
      result.add(currentPermutation);
    } else {
      // create a new permutation by adding the current number at every position
      for (int i = 0; i <= currentPermutation.size(); i++) {
        List<Integer> newPermutation = new ArrayList<Integer>(currentPermutation);
        newPermutation.add(i, nums[index]);
        generatePermutationsRecursive(nums, index + 1, newPermutation, result);
      }
    }
  }

  public static void main(String[] args) {
    List<List<Integer>> result = PermutationsRecursive.generatePermutations(new int[] { 1, 3, 5 });
    System.out.print("Here are all the permutations: " + result);
  }
}

// Output:
// Here are all the permutations: [[5, 3, 1], [3, 5, 1], [3, 1, 5], [5, 1, 3], [1, 5, 3], [1, 3, 5]]

LeetCode 784. Letter Case Permutation

Given a string S, we can transform every letter individually to be lowercase or uppercase to create another string. Return a list of all possible strings we could create.

Examples:
Input: S = "a1b2"
Output: ["a1b2", "a1B2", "A1b2", "A1B2"]

Input: S = "3z4"
Output: ["3z4", "3Z4"]

Input: S = "12345"
Output: ["12345"]

Note:

S will be a string with length between 1 and 12.
S will consist only of letters or digits.

Explanation

We can use BFS is putting the input string to the queue first.
Loop i through each character of the input string. If the current character is a digit, then we continue. Else, we loop j the current queue’s size, each time we poll the string out of the queue, then convert it to an array and update the index i character to lower case and append the updated string to the queue, similarlly, we also update the index i character to upper case and append the updated string to the queue.
At the end, the queue contains all the permutations.
For example, if the input string is abc, then we have:

[abc] put input string to the queue
[abc, Abc] updated index 0
[abc, aBc, Abc, ABc] updated index 1
[abc, abC, aBc, aBC, Abc, AbC, ABc, ABC] updated index 2

Solution

class Solution {
    public List<String> letterCasePermutation(String S) {
        if (S == null || S.length() == 0) return new LinkedList<>();

        Queue<String> queue = new LinkedList<>();
        queue.offer(S);

        for (int i = 0; i < S.length(); i++) {
            char cur = S.charAt(i);
            if (Character.isDigit(cur)) continue;

            int n = queue.size();
            for (int j = 0; j < n; j++) {
                String oldS = queue.poll();
                char[] arr = oldS.toCharArray();

                arr[i] = Character.toLowerCase(cur);
                queue.offer(String.valueOf(arr));

                arr[i] = Character.toUpperCase(cur);
                queue.offer(String.valueOf(arr));
            }
        }

        return new LinkedList<>(queue);
    }
}

LeetCode 301. Remove Invalid Parentheses

Remove the minimum number of invalid parentheses in order to make the input string valid. Return all possible results.

Note: The input string may contain letters other than the parentheses ( and ).

Example 1:

Input: "()())()"
Output: ["()()()", "(())()"]

Example 2:

Input: "(a)())()"
Output: ["(a)()()", "(a())()"]

Example 3:

Input: ")("
Output: [""]

Explanation

We can use BFS to solve this problem. First, add the input string to the queue. While the queue is not empty, we poll the string out, check if the poll string is valid. If the poll string is valid, then we add it to the result list and mark the variable found be true. Next, if found is true, we continue poll the queue. Else if found is false, then we loop through every character of the poll string. What we want is in each iteration, we remove a current iterated character to make a new string, then add this new string to the queue, and repeat until the queue is empty.

Solution

class Solution {
    boolean isValid(String s) {
        int cnt = 0;
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') cnt += 1;
            else if (s.charAt(i) == ')' && --cnt < 0) return false;
        }
        return cnt == 0;
    }

    public List<String> removeInvalidParentheses(String s) {
        List<String> res = new ArrayList<>();
        if (s == null) return res;

        Queue<String> queue = new LinkedList<>();
        Set<String> visited = new HashSet<>();
        boolean found = false;
        queue.offer(s);
        visited.add(s);

        while (!queue.isEmpty()) {
            String pollS = queue.poll();
            if (isValid(pollS)) {
                res.add(pollS);
                found = true;
            }
            if (found) continue;
            for (int i = 0; i < pollS.length(); i++) {
                if (pollS.charAt(i) != '(' && pollS.charAt(i) != ')') continue;
                String newS = pollS.substring(0, i) + pollS.substring(i+1, pollS.length());
                if (!visited.contains(newS)) {
                    queue.offer(newS);
                    visited.add(newS);
                }
            }
        }

        return res;
    }
}

LeetCode 320. Generalized Abbreviation

Write a function to generate the generalized abbreviations of a word.

Note: The order of the output does not matter.

Example:

Input: "word"
Output:
["word", "1ord", "w1rd", "wo1d", "wor1", "2rd", "w2d", "wo2", "1o1d", "1or1", "w1r1", "1o2", "2r1", "3d", "w3", "4"]

Explanation

We can solve this problem using BFS. First, we append an empty string to the queue.
Loop through every iterated character of the input string. Under each iteration, we loop every poll string in the queue. For each poll string, if the poll string ends with number, we will abbreviate the last number of the poll string with the iterated character and push back to the queue; we can also not abbreviate by just appending the iterated character to the end of the poll string and push back to the queue. Else if the poll string does not end with number, we will abbreviate by appending 1 to the end of the poll string and push back to the queue; we can also not abbreviate by just appending the iterated character to the end of the poll string and push back to the queue.
After we finish looping every character of the input string, we just return the queue which contains all the abbreviations.

Solution

class Solution {
    public List<String> generateAbbreviations(String word) {
        if (word == null) return new LinkedList<>();
        Queue<String> queue = new LinkedList<>();
        queue.offer("");
        for (int i = 0; i < word.length(); i++) {
            int n = queue.size();
            for (int j = 0; j < n; j++) {
                String pollS = queue.poll();
                char lastChar = ' ';
                if (pollS.length() > 0) {
                    lastChar = pollS.charAt(pollS.length()-1);
                }
                if (lastChar >= '0' && lastChar <= '9' ) {
                    queue.offer(pollS + word.charAt(i));

                    int lastCharIndex = pollS.length()-1;
                    for (lastCharIndex = pollS.length()-1; lastCharIndex >= 0; lastCharIndex--) {
                        if (!Character.isDigit(pollS.charAt(lastCharIndex))) break;
                    }
                    if (lastCharIndex == -1) {
                        queue.offer(String.valueOf(Integer.valueOf(pollS)+1));
                    } else {
                        queue.offer(pollS.substring(0, lastCharIndex+1) + String.valueOf(Integer.valueOf(pollS.substring(lastCharIndex+1))+1));
                    }
                } else {
                    queue.offer(pollS + word.charAt(i));
                    queue.offer(pollS + "1");
                }
            }
        }
        return new LinkedList<>(queue);
    }
}

Modified Binary Search

LeetCode 704. Binary Search

Given a sorted (in ascending order) integer array nums of n elements and a target value, write a function to search target in nums. If target exists, then return its index, otherwise return -1.

Example 1:

Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2:

Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

Note:

You may assume that all elements in nums are unique.
n will be in the range [1, 10000].
The value of each element in nums will be in the range [-9999, 9999].

Explanation

Standard binary search. First, initialize the range left = 0, right = nums.length-1. While left <= right, we find the middle index mid = left + (right - left) / 2. Then compare target with nums[mid]. If nums[mid] == target, we return mid. Else if nums[mid] < target, then we update left = mid + 1. Else if nums[mid] > target, then we update right = mid - 1.

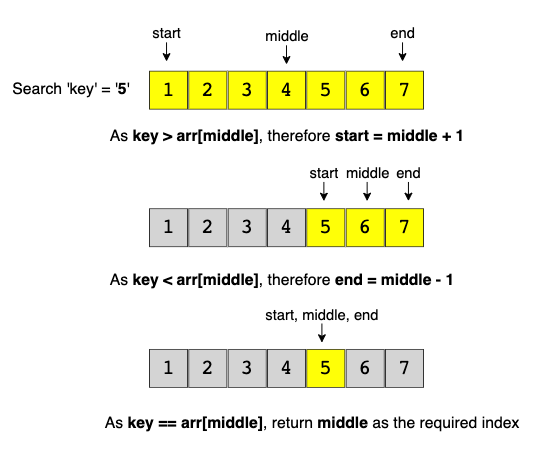
Source: Three Smart Ways to Use Binary Search in Coding Interviews

Solution

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }

        return -1;
    }
}

Ceiling of a Number

Given a sorted array of integers and an element K, return the index of the celing of K.

Ceiling of K is the smallest element in an array greater than or equal to K.

Example 1:

Input: nums = [-1,0,3,5,9,12], K = 7
Output: 4
Explanation: 9 is the celing of 7, and the index of 9 is 4.

Explanation

We can use binary search to solve this problem. While left <= right, if the middle index number is the ceiling arr[mid] >= target, then we update right = mid - 1, else we update left = mid + 1. Outside this while loop, we check arr[left] if it’s the ceiling, then we return its index, else there’s no ceiling so we return -1.

Solution

class Main {
    static int greater(int[] arr, int target) {
        int left = 0;
        int right = arr.length-1;
        while (left <= right) {
            int mid = left + ((right-left) >> 1);
            if (arr[mid] >= target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        if (arr[left] >= target) {
            return left;
        } else {
            return -1;
        }
    }
    public static void main (String[] args) {
        int[] arr = new int[] { -1, 0, 3, 5, 9, 12 };
        System.out.println(greater(arr, 7));
    }
}

LeetCode 744. Find Smallest Letter Greater Than Target

Given a list of sorted characters letters containing only lowercase letters, and given a target letter target, find the smallest element in the list that is larger than the given target.

Letters also wrap around. For example, if the target is target = 'z' and letters = ['a', 'b'], the answer is 'a'.

Examples:

Input:
letters = ["c", "f", "j"]
target = "a"
Output: "c"

Input:
letters = ["c", "f", "j"]
target = "c"
Output: "f"

Input:
letters = ["c", "f", "j"]
target = "d"
Output: "f"

Input:
letters = ["c", "f", "j"]
target = "g"
Output: "j"

Input:
letters = ["c", "f", "j"]
target = "j"
Output: "c"

Input:
letters = ["c", "f", "j"]
target = "k"
Output: "c"

Note:

letters has a length in range [2, 10000].
letters consists of lowercase letters, and contains at least 2 unique letters.
target is a lowercase letter.

Explanation

We can use binary search to find the first greater element in a sorted array. While left <= right, if arr[mid] <= target, then we update left = mid + 1; else we update right = mid - 1. Outside the while loop, we return arr[left]. In this problem, since the array is wrapped around, we can return arr[left % arr.size()].

Solution

class Solution {
    public char nextGreatestLetter(char[] letters, char target) {
        int left = 0, right = letters.length-1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (letters[mid] <= target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return letters[left % letters.length];
    }
}

LeetCode 34. Find First and Last Position of Element in Sorted Array

Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.

Your algorithm’s runtime complexity must be in the order of O(\log n).

If the target is not found in the array, return [-1, -1].

Example 1:

Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]

Example 2:

Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]

Explanation

Since we need to use $O(log n)$ runtime to solve this problem, we can use binary search to find the fist position, and use the binary search again to find the last position of the target.
To find the first position of the target, while left <= right, if nums[mid] >= target, we should move right to the left by right = mid - 1; else move left by left = mid + 1. Outside the while loop, left is pointing to the first position of the target. Before we return left, we need to check if left is less than the size of arr.
To find the last position of the target, while left <= right, if nums[mid] <= target, we should move left to the right by left = mid + 1; else move right by right = mid - 1. Outside the while loop, right is pointing to the last position of the target. Before we return right, we need to check if right is greater than or equal to 0.

Solution

class Solution {
    int findLeft(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        if (left < nums.length && nums[left] == target) return left;
        else return -1;
    }

    int findRight(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] <= target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        if (right >= 0 && nums[right] == target) return right;
        else return -1;
    }

    public int[] searchRange(int[] nums, int target) {
        int[] res = new int[] {-1, -1};
        if (nums == null || nums.length == 0) return res;
        int a = findLeft(nums, target);
        if (a == -1) return res;
        int b = findRight(nums, target);
        res[0] = a;
        res[1] = b;
        return res;
    }
}

LeetCode 702. Search in a Sorted Array of Unknown Size

Given an integer array sorted in ascending order, write a function to search target in nums. If target exists, then return its index, otherwise return -1. However, the array size is unknown to you. You may only access the array using an ArrayReader interface, where ArrayReader.get(k) returns the element of the array at index k (0-indexed).

You may assume all integers in the array are less than 10000, and if you access the array out of bounds, ArrayReader.get will return 2147483647.

Example 1:

Input: array = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2:

Input: array = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

Note:

You may assume that all elements in the array are unique.
The value of each element in the array will be in the range [-9999, 9999].

Explanation

Since the array has infinity size, we should first find the proper bounds of the array that the target is in between. Initially, we define left = 0 and right = 1, while reader.get(right) < target, we should exponentially increase the bound’s size, in other words, double the size until target is in between the bound.

Solution

class Solution {
    int binarySearch(ArrayReader reader, int target, int left, int right) {
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (reader.get(mid) == target) {
                return mid;
            } else if (reader.get(mid) < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;
    }

    public int search(ArrayReader reader, int target) {
        int left = 0, right = 1;
        while (reader.get(right) < target) {
            int newLeft = right + 1;
            right = right + (right - left + 1) * 2;
            left = newLeft;
        }
        return binarySearch(reader, target, left, right);
    }
}

Minimum Difference Element

Given an array of numbers sorted in ascending order. Find the element in the array that has the minimum difference with the given key. Assume there will be only 1 result.

Explanation

We can use binary search to solve this problem. If the arr[mid] == target, then we immediately return arr[mid]. Else if arr[mid] < target, then besides update left = mid + 1, we also calculate the difference between arr[mid] and target, if the difference is less than minDiff, then we update the minDiff and the result be arr[mid]. Similarlly, if arr[mid] > target, then besides update right = mid - 1, we also calculate the difference between arr[mid] and target, if the difference is less than minDiff, then we update the minDiff and the result be arr[mid].

Solution

class Main {
    static int solve(int[] arr, int target) {
        int left = 0, right = arr.length - 1;
        int minDiff = Integer.MAX_VALUE;
        int res = -1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (arr[mid] == target) {
                return arr[mid];
            } else if (arr[mid] < target) {
                if (target - arr[mid] < minDiff) {
                    res = arr[mid];
                    minDiff = target - arr[mid];
                }
                left = mid + 1;
            } else {
                if (arr[mid] - target < minDiff) {
                    res = arr[mid];
                    minDiff = arr[mid] - target;
                }
                right = mid - 1;
            }
        }
        return res;
    }

    public static void main (String[] args) {
        int[] arr = new int[] {1, 2, 3, 5, 5, 9};
        int target = 8;
        System.out.println(solve(arr, target));
    }
}

// Output:
// 9

LeetCode 162. Find Peak Element

A peak element is an element that is greater than its neighbors.

Given an input array nums, where nums[i] ≠ nums[i+1], find a peak element and return its index.

The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.

You may imagine that nums[-1] = nums[n] = -∞.

Example 1:

Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.

Example 2:

Input: nums = [1,2,1,3,5,6,4]
Output: 1 or 5
Explanation: Your function can return either index number 1 where the peak element is 2,
             or index number 5 where the peak element is 6.

Note:

Your solution should be in logarithmic complexity.

Explanation

First if the input array has size 1, then we return index 0 since nums[-1] = nums[n] = -∞.
We can use binary search to find the maximum element. We use while (left < right) since we compare nums[mid] and nums[mid+1]. If nums[mid+1] is greater, then we update left = mid + 1; else if nums[mid] <= nums[mid+1], then we update right = mid. Outside the while loop, nums[left] is pointing to the maximum element.

Solution

class Solution {
    public int findPeakElement(int[] nums) {
        if (nums == null) return -1;
        if (nums.length == 1) return 0;

        int left = 0, right = nums.length - 1;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < nums[mid+1]) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        return left;
    }
}

Bitwise XOR

LeetCode 136. Single Number

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Note:

Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory?

Example 1:

Input: [2,2,1]
Output: 1

Example 2:

Input: [4,1,2,1,2]
Output: 4

Explanation

We can use XOR to solve this problem. We know that 0 XOR 0 = 0, 1 XOR 1 = 0, 0 XOR 1 = 1 XOR 0 = 1. For example, we can initialize the res is 0000 first, loop through all the numbers, if the first number is 1010 then res XOR num = 0000 XOR 1010 = 1010. If the second number is also 1010, then res = res XOR num = 1010 XOR 1010 = 0000; If the third number is 1100, then the res = res XOR num = 0000 XOR 1100 = 1100. So we return the third number.

Solution

class Solution {
    public int singleNumber(int[] nums) {
        int res = 0;
        for (int num : nums) res ^= num;
        return res;
    }
}

LeetCode 260. Single Number III

Given an array of numbers nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.

Example:

Input:  [1,2,1,3,2,5]
Output: [3,5]

Note:

The order of the result is not important. So in the above example, [5, 3] is also correct.
Your algorithm should run in linear runtime complexity. Could you implement it using only constant space complexity?

Explanation

This problem asks us to find the two numbers (let say a and b) that are appear only once and they are different. If we want to use the XOR method by 136. Single Number, we need to seperate these two numbers into two different groups then apply the XOR method.
If we XOR all the numbers in the array, then the result will be xo = a ^ b because all other numbers are the same and appear twice and they will eventually become zero. Now, we want to seperate the array into two groups. Note, the xo cannot be zero here since a and b are different. We can use a bit as a seperate point, which is the xo right most non-zero bit as a seperate point. Because a and b on that bit will have different value. Note, the seperate point number will be only that bit is 1, other bit are 0. For example 00100.
We use this seperate number (let say diff) to AND all the numbers in the array. If the current iterated number AND this seperate number equals 0, then it’s one group; else equal 1, will be another group, since a and b on that bit are different.
We can use the XOR method to find that appeared only once number in a group to find a, and use the same method to find b in antoher group.
How do we find diff? After we XOR all numbers in the array to get xo, we use the formula diff = ~(xo-1) & xo to get diff. For example, if xo is 101100, then it subtract one equals 101011, not 101011 equals 010100. Then 010100 AND 101100 becomes 000100, which has only the right most 1 bit of xo.

Solution

class Solution {
    public int[] singleNumber(int[] nums) {
        int xo = 0;
        for (int num: nums) {
            xo ^= num;
        }
        int diff = ~(xo-1) & xo;
        int[] res = new int[2];
        for (int num: nums) {
            if ((num & diff) == 0) {
                res[0] ^= num;
            } else {
                res[1] ^= num;
            }
        }

        return res;
    }
}

LeetCode 1009. Complement of Base 10 Integer

Every non-negative integer N has a binary representation. For example, 5 can be represented as "101" in binary, 11 as "1011" in binary, and so on. Note that except for N = 0, there are no leading zeroes in any binary representation.

The complement of a binary representation is the number in binary you get when changing every 1 to a 0 and 0 to a 1. For example, the complement of "101" in binary is "010" in binary.

For a given number N in base-10, return the complement of it’s binary representation as a base-10 integer.

Example 1:

Input: 5
Output: 2
Explanation: 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10.

Example 2:

Input: 7
Output: 0
Explanation: 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10.

Example 3:

Input: 10
Output: 5
Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.

Note:

0 <= N < 10^9

Explanation

In order to make 101 becomes 010, we can just do 101 ^ 111 = 010. Similarlly, 111 ^ 111 = 000, and 1010 ^ 1111 = 0101.
From the above example, we know that we first need to find the smallest number a that has all bits set to 1 and a <= N. Initially, we define a = 1, while a < N, then we do a = (a << 1) + 1 or a = (a << 1) | 1. Outside the while loop, we return the result a ^ N.

Solution

class Solution {
    public int bitwiseComplement(int N) {
        int a = 1;
        while (a < N) {
            a = (a << 1) | 1;
        }
        return a ^ N;
    }
}

Top ‘K’ Elements

LeetCode 215. Kth Largest Element in an Array

Find the kth largest element in an unsorted array. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Example 1:

Input: [3,2,1,5,6,4] and k = 2
Output: 5

Example 2:

Input: [3,2,3,1,2,4,5,5,6] and k = 4
Output: 4

Note:

You may assume k is always valid, 1 ≤ k ≤ array’s length.

Explanation

We can use quick sort’s partition function to solve this problem in $O(1)$ time complexity because partition function return us the correct index, where all elements on the left side of the index are greather than this index number, all elements are on the right side of this index number are less than this index number. Note, we are sorting from largest to smallest.
First, we make a left pointer and right pointer that point to index 0 and the right most index. If the partition function return us p which equals to k-1, then we return nums[k-1]. Else if k-1 is greather than p, then left pointer moves to p+1, else if k-1 is smaller than p, then right pointer moves to p-1.
Inside the partition function, we first mark the first element as pivot. Left pointer moves one step forward, which is left+1, right poitner is the last index. While left pointer is smaller or equal to the right pointer, we start a while loop. If the left pointer number is smaller than the value of pivot and right pointer value is greather than pivot value, swap the left pointer and right pointer value. Then, if the left pointer value is greater or equal to the pivot value, then left pointer move right one step. If the right pointer value is smaller or equal than pivot, then right pointer value move left one step.
Out of the while loop, we swap pivot and the right pointer. Now, pivot is at its correct index. We finally return its index, which is the right pointer.

Solution

class Solution {
    void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }

    int partition(int[] nums, int start, int end) {
        int pivot = nums[start];
        int left = start + 1;
        int right = end;
        while (left <= right) {
            if (nums[left] < pivot && nums[right] > pivot) {
                swap(nums, left, right);
            }
            if (nums[left] >= pivot) left += 1;
            if (nums[right] <= pivot) right -= 1;
        }
        swap(nums, start, right);
        return right;
    }

    public int findKthLargest(int[] nums, int k) {
        int start = 0, end = nums.length - 1;
        while (start <= end) {
            int p = partition(nums, start, end);
            if (k-1 == p) return nums[k-1];
            else if (p > k-1) end = p-1;
            else if (p < k-1) start = p+1;
        }

        return -1;
    }
}

Kth Smallest Number

Given an array and a number k where k is smaller than the size of the array, we need to find the k’th smallest element in the given array. It is given that all array elements are distinct.

Examples:

Input: arr[] = {7, 10, 4, 3, 20, 15}
       k = 3
Output: 7

Input: arr[] = {7, 10, 4, 3, 20, 15}
       k = 4
Output: 10

Source: K’th Smallest/Largest Element in Unsorted Array Set 1

Explanation

Loop through the array, putting the first k elements into the max-heap. For the rest of numbers in the array, in each iteration, we compare the iterated number with the top or maximum number of the max-heap. If the iterated number is smaller, then we extract out the top element of the max-heap, and put the iterated number into the max-heap.

Solution

import java.util.*;

class Main {
    public static int findKthSmallest(int[] arr, int k) {
        Queue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());
        for (int i = 0; i < k; i++) {
            pq.offer(arr[i]);
        }

        for (int i = k; i < arr.length; i++) {
            if (arr[i] < pq.peek()) {
                pq.poll();
                pq.offer(arr[i]);
            }
        }

        return pq.peek();
    }

    public static void main(String[] args) {
        int[] arr = new int[] {7, 5, 6, 3, 9, 1};
        int k = 3;
        System.out.println("K'th smallest element in the array is " + findKthSmallest(arr, k));
    }
}

// Output:
// K'th smallest element in the array is 5

LeetCode 973. K Closest Points to Origin

We have a list of points on the plane. Find the K closest points to the origin (0, 0).

(Here, the distance between two points on a plane is the Euclidean distance.)

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in.)

Example 1:

Input: points = [[1,3],[-2,2]], K = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest K = 1 points from the origin, so the answer is just [[-2,2]].

Example 2:

Input: points = [[3,3],[5,-1],[-2,4]], K = 2
Output: [[3,3],[-2,4]]
(The answer [[-2,4],[3,3]] would also be accepted.)

Note:

1 <= K <= points.length <= 10000
-10000 < points[i][0] < 10000
-10000 < points[i][1] < 10000

Explanation

This problem asks us to find the first K short distance points and return them without sorting, so we can use quick select method to solve this problem in $O(N)$ average time complexity.

Solution

class Solution {
    double calc(int[] point) {
        int x = point[0];
        int y = point[1];
        return Math.sqrt(x * x + y * y);
    }

    void swap(int[][] points, int a, int b) {
        int ax = points[a][0];
        int ay = points[a][1];
        points[a][0] = points[b][0];
        points[a][1] = points[b][1];
        points[b][0] = ax;
        points[b][1] = ay;
    }

    int partition(int[][] points, int start, int end) {
        double pivotDist = calc(points[start]);
        int left = start + 1;
        int right = end;
        while (left <= right) {
            double leftDist = calc(points[left]);
            double rightDist = calc(points[right]);
            if (leftDist > pivotDist && rightDist < pivotDist) {
                swap(points, left, right);
                double temp = leftDist;
                leftDist = rightDist;
                rightDist = temp;
            }
            if (leftDist <= pivotDist) left += 1;
            if (rightDist >= pivotDist) right -= 1;
        }
        swap(points, start, right);
        return right;
    }

    public int[][] kClosest(int[][] points, int K) {
        int left = 0, right = points.length - 1;
        while (left <= right) {
            int p = partition(points, left, right);
            if (p == K-1) {
                return Arrays.copyOfRange(points, 0, K);
            } else if (p < K-1) {
                left = p + 1;
            } else {
                right = p - 1;
            }
        }
        return new int[0][0];
    }
}

LeetCode 1167. Minimum Cost to Connect Sticks

You have some sticks with positive integer lengths.

You can connect any two sticks of lengths X and Y into one stick by paying a cost of X + Y. You perform this action until there is one stick remaining.

Return the minimum cost of connecting all the given sticks into one stick in this way.

Example 1:

Input: sticks = [2,4,3]
Output: 14

Example 2:

Input: sticks = [1,8,3,5]
Output: 30

Constraints:

1 <= sticks.length <= 10^4
1 <= sticks[i] <= 10^4

Explanation

Everytime we want to connect the two shortest sticks first, then put the connected sticks back, and repeat this process.
We can use min-heap to solve this problem. First put the array of integers into a min-heap. While the heap has size more than 1, we want to extract 2 minimum integers out of the heap and sum them, update the result, then put the sum back to the heap.

Solution

class Solution {
    public int connectSticks(int[] sticks) {
        int res = 0;
        Queue<Integer> pq = new PriorityQueue<>();
        for (int stick: sticks) pq.offer(stick);

        while (pq.size() > 1) {
            int sum = pq.poll() + pq.poll();
            res += sum;
            pq.offer(sum);
        }

        return res;
    }
}

LeetCode 347. Top K Frequent Elements

Given a non-empty array of integers, return the k most frequent elements.

Example 1:

Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]

Example 2:

Input: nums = [1], k = 1
Output: [1]

Note:

You may assume k is always valid, 1 ≤ k ≤ number of unique elements.
Your algorithm’s time complexity must be better than O(n log n), where n is the array’s size.

Explanation

We can use bucket sort with $O(n)$ runtime to solve this problem.
First, we create a hashmap to store each number and its frequency. Then, we find out the maximum frequency, and use the maximum frequency as the length of a new array. The array will have length maximum frequency plus one, since we want the maximum frequency is the last index of this array.
Each array element will be a new array list. Then, we loop through the HashMap, put the entry’s frequency as the array’s index, number will add it to the list arr[i].
Now, we can loop from the back of the array to front, for each arraylist arr[i], we store their number into our res list until the res list has size k.

Solution

class Solution {
    public List<Integer> topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> hm = new HashMap<>();
        for (int num: nums) {
            hm.put(num, hm.getOrDefault(num, 0)+1);
        }

        int mx = 0;
        for (Map.Entry<Integer, Integer> e: hm.entrySet()) {
            mx = Math.max(mx, e.getValue());
        }

        List<Integer>[] arr = new List[mx + 1];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = new ArrayList<>();
        }

        for (Map.Entry<Integer, Integer> e: hm.entrySet()) {
            int num = e.getKey();
            int freq = e.getValue();
            arr[freq].add(num);
        }

        List<Integer> res = new ArrayList<>();
        for (int i = mx; i >= 0; i--) {
            for (int a: arr[i]) {
                if (res.size() == k) {
                    return res;
                }
                res.add(a);
            }
        }

        return res;
    }
}

LeetCode 451. Sort Characters By Frequency

Given a string, sort it in decreasing order based on the frequency of characters.

Example 1:

Input:
"tree"

Output:
"eert"

Explanation:
'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr" is also a valid answer.

Example 2:

Input:
"cccaaa"

Output:
"cccaaa"

Explanation:
Both 'c' and 'a' appear three times, so "aaaccc" is also a valid answer.
Note that "cacaca" is incorrect, as the same characters must be together.

Example 3:

Input:
"Aabb"

Output:
"bbAa"

Explanation:
"bbaA" is also a valid answer, but "Aabb" is incorrect.
Note that 'A' and 'a' are treated as two different characters.

Explanation

We can also use bucket sort to solve this problem. First, we store the character and its frequency to a HashMap. Next, we create an array of list. Iterate the HashMap, for each entry, its frequency will be the array’s index, its key, in other words, the character will be added to the list on that index.
Next, we iterate the array from right to left, if the element on the current index is null, that means there’s no list, so we continue. Else, the current index has a list, then we append the list’s character the number of index times to the StringBuilder.

Solution

class Solution {
    public String frequencySort(String s) {
        Map<Character, Integer> hm = new HashMap<>();
        char[] arr = s.toCharArray();
        for (char c: arr) {
            hm.put(c, hm.getOrDefault(c, 0)+1);
        }
        List<Character>[] buckets = new List[s.length()+1];
        for (Map.Entry<Character, Integer> e: hm.entrySet()) {
            int idx = e.getValue();
            char c = e.getKey();
            if (buckets[idx] == null) buckets[idx] = new ArrayList<>();
            buckets[idx].add(c);
        }

        StringBuilder sb = new StringBuilder();
        for (int i = buckets.length-1; i >= 0; i--) {
            if (buckets[i] == null) continue;
            for (Character c: buckets[i]) {
                for (int j = 0; j < i; j++) {
                    sb.append(c);
                }
            }
        }

        return sb.toString();
    }
}

LeetCode 703. Kth Largest Element in a Stream

Design a class to find the kth largest element in a stream. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Your KthLargest class will have a constructor which accepts an integer k and an integer array nums, which contains initial elements from the stream. For each call to the method KthLargest.add, return the element representing the kth largest element in the stream.

Example:

int k = 3;
int[] arr = [4,5,8,2];
KthLargest kthLargest = new KthLargest(3, arr);
kthLargest.add(3);   // returns 4
kthLargest.add(5);   // returns 5
kthLargest.add(10);  // returns 5
kthLargest.add(9);   // returns 8
kthLargest.add(4);   // returns 8

Note:

You may assume that nums’ length ≥ k-1 and k ≥ 1.

Explanation

Similar to LeetCode 215. Kth Largest Element in an Array, the difference is in this problem, the size of the stream is unknown. We can solve it using a min heap with size k. If the heap has size more than k, we pop out the min value to maintain all elements in the heap are the K largest elements.

Solution

class KthLargest {
    Queue<Integer> pq;
    int k;

    public KthLargest(int k, int[] nums) {
        this.pq = new PriorityQueue<>();
        this.k = k;
        for (int n: nums) {
            pq.offer(n);
            if (pq.size() > k) pq.poll();
        }
    }

    public int add(int val) {
        pq.offer(val);
        if (pq.size() > k) pq.poll();
        return pq.peek();
    }
}

/**
 * Your KthLargest object will be instantiated and called as such:
 * KthLargest obj = new KthLargest(k, nums);
 * int param_1 = obj.add(val);
 */

LeetCode 658. Find K Closest Elements

Given a sorted array, two integers k and x, find the k closest elements to x in the array. The result should also be sorted in ascending order. If there is a tie, the smaller elements are always preferred.

Example 1:

Input: [1,2,3,4,5], k=4, x=3
Output: [1,2,3,4]

Example 2:

Input: [1,2,3,4,5], k=4, x=-1
Output: [1,2,3,4]

Note:

The value k is positive and will always be smaller than the length of the sorted array.
Length of the given array is positive and will not exceed 104
Absolute value of elements in the array and x will not exceed 104

UPDATE (2017/9/19):

The arr parameter had been changed to an array of integers (instead of a list of integers). Please reload the code definition to get the latest changes.

Explanation

Since the array is sorted, we can use binary search. We are trying to use binary search to find the starting index of the result array. So the range of the starting index will be left=0 to right=arr.length-k inclusive.
While left < right, we calculate the mid as the starting index of the result array and arr[mid+k] as the next k positions’ starting index. Then we compare the difference between x-arr[mid] and arr[mid+k]-x. If the difference between arr[mid] and x is greater, we move left to the right side. Else we move right to the left side.
When left == right, that means we find the starting index of the result array. So we starting from this index and loop till index left + k and adding all these iterated elements to the result array.

Solution

class Solution {
    public List<Integer> findClosestElements(int[] arr, int k, int x) {
        int left = 0, right = arr.length - k;
        while (left < right) {
            int mid = left + (right - left) / 2;
            if (x - arr[mid] > arr[mid+k] - x) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        int[] res = Arrays.copyOfRange(arr, left, left + k);
        return Arrays.stream(res).boxed().collect(Collectors.toList());
    }
}

Maximum Distinct Elements

Given an array arr[] containing n elements. The problem is to find maximum number of distinct elements (non-repeating) after removing k elements from the array.

Note: 1 <= k <= n.

Example:

Input : arr[] = {5, 7, 5, 5, 1, 2, 2}, k = 3
Output : 4
Remove 2 occurrences of element 5 and
1 occurrence of element 2.

Input : arr[] = {1, 2, 3, 4, 5, 6, 7}, k = 5
Output : 2

Input : arr[] = {1, 2, 2, 2}, k = 1
Output : 1

Source: Maximum distinct elements after removing k elements

Explanation

Create a hashmap and store all the array elements’ frequency.
Loop through the hashmap, if the entry has frequency 1, then we increase the result. Else, we push the entry’s frequency into a min-heap.
While k > 0 and the min-heap is not empty, we extract the minimum frequency out and decrease it by 1. If the updated extracted frequency is equal to 1, then we increase the result; else we push back the updated extracted frequency into the min-heap.
Outside the while loop, we return the result.

Solution

import java.util.*;

class Main {
    static int maxDistinctNum(int[] arr, int k) {
        int res = 0;
        Map<Integer, Integer> hm = new HashMap<>();
        Queue<Integer> pq = new PriorityQueue<>();

        for (int i = 0; i < arr.length; i++) {
            hm.put(arr[i], hm.getOrDefault(arr[i], 0) + 1);
        }

        for (Map.Entry<Integer, Integer> entry : hm.entrySet()) {
            int freq = entry.getValue();
            if (freq == 1) {
                res += 1;
            } else {
                pq.offer(freq);
            }
        }

        while (k > 0 && !pq.isEmpty()) {
            int pollFreq = pq.poll();
            pollFreq -= 1;
            if (pollFreq == 1) {
                res += 1;
            } else {
                pq.offer(pollFreq);
            }
            k -= 1;
        }

        return res;
    }

    public static void main(String args[]) {
        int[] arr = { 5, 7, 5, 5, 1, 2, 2 };
        int k = 3;
        System.out.println("Maximum distinct elements = " +  maxDistinctNum(arr, k));
    }
}

// Output:
// Maximum distinct elements = 4

Sum of Elements

Given an array of integers and two numbers k1 and k2. Find the sum of all elements between given two k1’th and k2’th smallest elements of the array. It may be assumed that (1 <= k1 < k2 <= n) and all elements of array are distinct.

Examples :

Input : arr[] = {20, 8, 22, 4, 12, 10, 14},  k1 = 3,  k2 = 6
Output : 26
         3rd smallest element is 10. 6th smallest element
         is 20. Sum of all element between k1 & k2 is
         12 + 14 = 26

Input : arr[] = {10, 2, 50, 12, 48, 13}, k1 = 2, k2 = 6
Output : 73

Source: Sum of all elements between k1’th and k2’th smallest elements

Explanation 1

Sort the array. Then loop through the array from index k1 to index k2-2 inclusive and sum the iterated elements.

Solution 1

import java.util.*;

class Main {
    static int sumBetweenTwoKth(int arr[], int k1, int k2) {
        int res = 0;
        Arrays.sort(arr);
        for (int i = k1; i <= k2 - 2; i++) res += arr[i];
        return res;
    }

    public static void main(String[] args) {
        int arr[] = { 20, 8, 22, 4, 12, 10, 14 };
        int k1 = 3, k2 = 6;
        System.out.print(sumBetweenTwoKth(arr, k1, k2));
    }
}

// Output:
// 26

Explanation 2

Create a min-heap for all array elements. (This takes O(n) time).
Extract the minimum element k1 times (This takes O(k1 Log n) time).
Extract the minimum element k2 – k1 – 1 times and sum all these extracted elements. (This takes O ((k2 – k1) * Log n) time).

Solution 2

class Main {
    static void minHeapify(int[] arr, int rootIdx, int n) {
        int small = rootIdx;
        int left = 2 * rootIdx + 1;
        int right = 2 * rootIdx + 2;

        if (left < n && arr[left] < arr[small]) small = left;
        if (right < n && arr[right] < arr[small]) small = right;

        if (small != rootIdx) {
            int temp = arr[small];
            arr[small] = arr[rootIdx];
            arr[rootIdx] = temp;
            minHeapify(arr, small, n);
        }
    }

    static void buildMinHeap(int[] arr) {
        for (int i = (arr.length / 2) - 1; i >= 0; i--) {
            minHeapify(arr, i, arr.length);
        }
    }

    static int sumBetweenTwoKth(int arr[], int k1, int k2) {
        int res = 0;
        int n = arr.length;

        buildMinHeap(arr);

        for (int i = 0; i < k1; i++) {
            arr[0] = arr[n - 1];
            n--;
            minHeapify(arr, 0, n);
        }

        for (int i = 0; i < (k2 - k1 - 1); i++) {
            res += arr[0];
            arr[0] = arr[n - 1];
            n--;
            minHeapify(arr, 0, n);
        }

        return res;
    }

    public static void main (String[] args) {
        int k1 = 3;
        int k2 = 6;
        int [] arr = { 20, 8, 22, 4, 12, 10, 14 };
        System.out.println(sumBetweenTwoKth(arr, k1, k2));
    }
}

// Output:
// 26

LeetCode 767. Reorganize String

Given a string S, check if the letters can be rearranged so that two characters that are adjacent to each other are not the same.

If possible, output any possible result. If not possible, return the empty string.

Example 1:

Input: S = "aab"
Output: "aba"

Example 2:

Input: S = "aaab"
Output: ""

Note:

S will consist of lowercase letters and have length in range [1, 500].

Explanation

First getting every character’s frequency. Then we append the highest frequency character to the result StringBuilder first, the second highest frequency frequency character to the result StringBuilder second. After we appending these two characters, we update their frequency and repeat this process.
To achieve the above implementation, we need to create a new class which grouping the character and its frequency, and we need a priority queue to store the grouping and sorting by highest frequency in front.
The result will be an empty string only if any of the character frequency is higher than half of the string length. So before we append the grouping to the priority queue, we check if the result will be an empty string.

Solution

class CharFreq {
    char ch;
    int freq;

    CharFreq(char ch, int freq) {
        this.ch = ch;
        this.freq = freq;
    }
}

class Solution {
    public String reorganizeString(String S) {
        int[] count = new int[26];
        for (char c: S.toCharArray()) {
            count[c - 'a'] += 1;
        }
        PriorityQueue<CharFreq> pq = new PriorityQueue<>((a, b) -> a.freq == b.freq ? a.ch - b.ch : b.freq - a.freq);

        for (int i = 0; i < 26; i++) {
            if (count[i] == 0) continue;
            if (count[i] > (S.length() + 1) / 2) return "";
            pq.offer(new CharFreq((char)(i+'a'), count[i]));
        }

        StringBuilder res = new StringBuilder();
        while (pq.size() >= 2) {
            CharFreq a = pq.poll();
            CharFreq b = pq.poll();
            res.append(a.ch);
            res.append(b.ch);
            if (--a.freq > 0) pq.offer(a);
            if (--b.freq > 0) pq.offer(b);
        }

        if (pq.size() == 1) res.append(pq.poll().ch);

        return res.toString();
    }
}

K-way merge

LeetCode 23. Merge k Sorted Lists

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

Example:

Input:
[
  1->4->5,
  1->3->4,
  2->6
]
Output: 1->1->2->3->4->4->5->6

Explanation 1

We can use divide and conquer method to solve this problem. For example, if we have 6 ListNode, then we can solve ListNode1 with ListNode4, ListNode2 with ListNode5, ListNode3 with ListNode6.
Then, we have 3 ListNode need to sort. We then sort ListNode1 with ListNode3.
Then, we have 2 ListNode need to sort. We then sort ListNode1 with ListNode2.
Finally, we return the result of ListNode1.
Since there are $k$ ListNode in the array, similarly to merge sort, we divide $k$ ListNode takes $\log(k)$ time, and there are total of $kn$ nodes to compare, so the total time complexity is $kn\log(k)$. The space complexity is $log(k)$ because of the recursive stack.

Solution 1

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) return l2;
        if (l2 == null) return l1;
        if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }

    public ListNode mergeKLists(ListNode[] lists) {
        int n = lists.length;
        if (n < 1) return null;
        if (n == 1) return lists[0];
        while (n >= 2) {
            int mid = (n+1)/2;
            for (int i = 0; i < n/2; i++) {
                lists[i] = mergeTwoLists(lists[i], lists[i+mid]);
            }
            n = mid;
        }
        return lists[0];
    }
}

// Iterated way of merging 2 ListNode

// class Solution {
//     ListNode merge(ListNode list1, ListNode list2) {
//         ListNode dummy = new ListNode(-1);
//         ListNode pre = dummy;
//         ListNode ptr1 = list1, ptr2 = list2;
//         pre.next = ptr1;
//         while (ptr1 != null && ptr2 != null) {
//             if (ptr1.val < ptr2.val) {
//                 ptr1 = ptr1.next;
//             } else {
//                 ListNode nex = ptr2.next;
//                 pre.next = ptr2;
//                 ptr2.next = ptr1;
//                 ptr2 = nex;
//             }
//             pre = pre.next;
//         }
//         if (ptr2 != null) {
//             pre.next = ptr2;
//         }
//         return dummy.next;
//     }

//     ListNode helper(ListNode[] lists, int left, int right) {
//         while (left < right) {
//             int mid = left + (right - left) / 2;
//             return merge(helper(lists, left, mid), helper(lists, mid+1, right));
//         }
//         return lists[left];
//     }

//     public ListNode mergeKLists(ListNode[] lists) {
//         if (lists.length == 0) return null;
//         if (lists.length == 1) return lists[0];
//         return helper(lists, 0, lists.length - 1);
//     }
// }

Explanation 2

We can create a min-heap by using the PriorityQueue data structure to store all ListNode. If there are $k$ ListNode inside the input array, then we store all $k$ ListNode. They are sorted by their first Node value.
We create a res ListNode, then extract the minimum ListNode and put it’s value into the res ListNode. If the extracted ListNode’s next node is not empty, put it back to the priority queue. Repeat this process until the priority queue is empty.
Finally return the res ListNode.
Since there are $k$ ListNode in the array, and there are $n$ ListNode in each ListNode, so there are total of $kn$ elements in the array. Because each element adding to the queue costs $log(k)$ time, so the total time complexity is $kn\log(k)$. The space complexity is $O(k)$ because of the min-heap size will have maximum $k$ ListNodes.

Solution 2

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists.length == 0) return null;
        if (lists.length == 1) return lists[0];
        Queue<ListNode> pq = new PriorityQueue<>((a, b) -> {
            return a.val - b.val;
        });

        for (ListNode list: lists) {
            if (list != null) pq.offer(list);
        }

        ListNode dummy = new ListNode(-1);
        ListNode pre = dummy;
        while (!pq.isEmpty()) {
            ListNode pollNode = pq.poll();
            pre.next = pollNode;
            pre = pre.next;
            if (pollNode.next != null) {
                pq.offer(pollNode.next);
            }
        }

        return dummy.next;
    }
}

Kth Smallest Number in M Sorted Lists

Given M sorted arrays of possibly different sizes, find K-th smallest value in the merged array.

Examples:

Input: K = 5
       lists[][] = {
                    {1, 3},
                    {2, 4, 6},
                    {0, 9, 10, 11}
                   };
Output: 4
Explanation: The merged array would be {0 1 2 3 4 6 9 10 11}.
The 5-th smallest element in this merged array is 4.

Input: K = 6
      lists[][] = {
                    {1, 3, 20},
                    {2, 4, 6}
                  };
Output: 20

Explanation

Create a min-heap of size M, then put the first element of every sorted list into the min-heap.
Loop K-1 times, in each iteration, we pop the minimum element out of the heap and insert the pop element’s next element into the min-heap.
After looping K-1 times, the Kth smallest element will be the top element in the min-heap.

Solution

import java.util.*;

class EleIdx {
    int ele;
    int idx;
    int subIdx;

    EleIdx(int ele, int idx, int subIdx) {
        this.ele = ele;
        this.idx = idx;
        this.subIdx = subIdx;
    }
}

class Main {
    static int kthSmallest(List<List<Integer>> lists, int k) {
        Queue<EleIdx> pq = new PriorityQueue<>((a, b) -> {
            return a.ele - b.ele;
        });
        for (int i = 0; i < lists.size(); i++) {
            List<Integer> curList = lists.get(i);
            if (!curList.isEmpty()) {
                pq.offer(new EleIdx(curList.get(0), i, 0));
            }
        }
        for (int i = 0; i < k-1; i++) {
            EleIdx pollEleIdx = pq.poll();
            List<Integer> pollList = lists.get(pollEleIdx.idx);
            if (pollEleIdx.subIdx+1 < pollList.size()) {
                pq.offer(new EleIdx(pollList.get(pollEleIdx.subIdx+1), pollEleIdx.idx, pollEleIdx.subIdx+1));
            }
        }
        return pq.peek().ele;
    }

    public static void main(String[] args) {
        List<List<Integer>> lists = new ArrayList<>();
        lists.add(new ArrayList<>(Arrays.asList(1, 3)));
        lists.add(new ArrayList<>(Arrays.asList(2, 4, 6)));
        lists.add(new ArrayList<>(Arrays.asList(0, 9, 10, 11)));
        System.out.println(kthSmallest(lists, 7));
    }
}

// Output:
// 9

Kth Smallest Number in a Sorted Matrix

Given an N ∗ N matrix where each row and column is sorted in ascending order, find the Kth smallest element in the matrix.

Example 1:

Input: Matrix=[
    [2, 6, 8],
    [3, 7, 10],
    [5, 8, 11]
  ],
  K=5
Output: 7
Explanation: The 5th smallest number in the matrix is 7.

Explanation 1

As each row (or column) of the given matrix can be seen as a sorted list, we essentially need to find the Kth smallest number in N sorted lists.
We can create a class Node to record the row and column. Row is the index for the sublist, col is the index for the element in the sublist. We also create a min-heap to store the Node and sort by their element from smallest to largest.
We put the first element as a new Node of each sublist into the min-heap. While the min-heap is not empty, we extract the minimum Node out, then update the result be matrix[Node.row][Node.col]. Then increase the counter, if the counter is K, then we break out this while loop and return the result. Else, we increase the extracted Node’s col, check if the updated col is less than its corresponding subist’s length, then we push the updated extracted Node back into the min-heap.
Time complexity. First, we inserted at most K or one element from each of the N rows, which will take $O(min(K, N))$. Then we went through at most K elements in the matrix and remove/add one element in the heap in each step. As we can’t have more than N elements in the heap in any condition, therefore, the overall time complexity of the above algorithm will be $O(min(K, N) + K log N)$.
Space complexity. The space complexity will be $O(N)$ because, in the worst case, our min-heap will be storing one number from each of the N rows.

Solution 1

import java.util.*;

class Node {
  int row;
  int col;

  Node(int row, int col) {
    this.row = row;
    this.col = col;
  }
}

class Main {
  public static int findKthSmallest(int[][] matrix, int k) {
    PriorityQueue<Node> minHeap = new PriorityQueue<Node>((n1, n2) -> matrix[n1.row][n1.col] - matrix[n2.row][n2.col]);

    for (int i = 0; i < matrix.length && i < k; i++) {
      minHeap.add(new Node(i, 0));
    }

    int numberCount = 0, result = 0;
    while (!minHeap.isEmpty()) {
      Node node = minHeap.poll();
      result = matrix[node.row][node.col];
      if (++numberCount == k) break;
      node.col++;
      if (matrix[0].length > node.col) minHeap.add(node);
    }
    return result;
  }

  public static void main(String[] args) {
    int matrix[][] = { { 2, 6, 8 }, { 3, 7, 10 }, { 5, 8, 11 } };
    int result = Main.findKthSmallest(matrix, 5);
    System.out.print("Kth smallest number is: " + result);
  }
}

// Output:
// Kth smallest number is: 7

Explanation 2

We apply the Binary Search on the “number range” instead of the “index range”. As we know that the smallest number of our matrix is at the top left corner and the biggest number is at the bottom right corner. These two numbers can represent the “range” i.e., the start and the end for the Binary Search.
Start the Binary Search with start = matrix[0][0] and end = matrix[n-1][n-1].
Find middle of the start and the end. This middle number is NOT necessarily an element in the matrix.
Count all the numbers smaller than or equal to middle in the matrix. As the matrix is sorted, we can do this in $O(N)$.
While counting, we can keep track of the “smallest number greater than the middle” (let’s call it n1) and at the same time the “biggest number less than or equal to the middle” (let’s call it n2). These two numbers will be used to adjust the “number range” for the Binary Search in the next iteration.
If the count is equal to K, n1 will be our required number as it is the “biggest number less than or equal to the middle”, and is definitely present in the matrix.
If the count is less than K, we can update start = n2 to search in the higher part of the matrix and if the count is greater than K, we can update end = n1 to search in the lower part of the matrix in the next iteration.

Solution 2

class Main {
  public static int findKthSmallest(int[][] matrix, int k) {
    int n = matrix.length;
    int start = matrix[0][0], end = matrix[n - 1][n - 1];
    while (start < end) {
      int mid = start + (end - start) / 2;
      int[] smallLargePair = { matrix[0][0], matrix[n - 1][n - 1] };
      int count = countLessEqual(matrix, mid, smallLargePair);
      if (count == k)
        return smallLargePair[0];
      if (count < k)
        start = smallLargePair[1]; // search higher
      else
        end = smallLargePair[0]; // search lower
    }

    return start;
  }

  private static int countLessEqual(int[][] matrix, int mid, int[] smallLargePair) {
    int count = 0;
    int n = matrix.length, row = n - 1, col = 0;
    while (row >= 0 && col < n) {
      if (matrix[row][col] > mid) {
        smallLargePair[1] = Math.min(smallLargePair[1], matrix[row][col]);
        row--;
      } else {
        smallLargePair[0] = Math.max(smallLargePair[0], matrix[row][col]);
        count += row + 1;
        col++;
      }
    }
    return count;
  }

  public static void main(String[] args) {
    int matrix[][] = { { 1, 4 }, { 2, 5 } };
    int result = Main.findKthSmallest(matrix, 2);
    System.out.println("Kth smallest number is: " + result);

    int matrix1[][] = { { -5 } };
    result = Main.findKthSmallest(matrix1, 1);
    System.out.println("Kth smallest number is: " + result);

    int matrix2[][] = { { 2, 6, 8 }, { 3, 7, 10 }, { 5, 8, 11 } };
    result = Main.findKthSmallest(matrix2, 5);
    System.out.println("Kth smallest number is: " + result);

    int matrix3[][] = { { 1, 5, 9 }, { 10, 11, 13 }, { 12, 13, 15 } };
    result = Main.findKthSmallest(matrix3, 8);
    System.out.println("Kth smallest number is: " + result);

  }
}

// Output:
// Kth smallest number is: 2
// Kth smallest number is: -5
// Kth smallest number is: 7
// Kth smallest number is: 13

Source: Kth Smallest Number in a Sorted Matrix (Hard)

LeetCode 632. Smallest Range Covering Elements from K Lists

You have k lists of sorted integers in ascending order. Find the smallest range that includes at least one number from each of the k lists.

We define the range [a,b] is smaller than range [c,d] if b-a < d-c or a < c if b-a == d-c.

Explanation

First, we put all the sublists’ first number into a min-heap. While we putting the first number, we also record the maximum number curMax. After finishing putting the first numbers, we can calculate the diff which is the maximum number subtract the top number of the min-heap. Also, we can initalize the result range be the min-heap’s top number and the curMax.
Now, while the min-heap’s top element is not the last element in its corresponding list, we extract out the minimum number from the min-heap. Then we get the next number from the extracted number’s list, and compare it with curMax to update curMax. After comparing, we put that next number into the min-heap. Then, we calculate the newDiff by curMax subtract the top element of the min-heap. If the newDiff is less than diff, then we update diff = newDiff and the result range be top element of the min-heap and curMax.
The time complexity is the O(N * log K) where N is the maximum size of the sublists and K is the nubmer of sub-lists.

Solution

class Node {
    int row;
    int col;
    Node (int row, int col) {
        this.row = row;
        this.col = col;
    }
}

class Solution {
    public int[] smallestRange(List<List<Integer>> nums) {
        int[] res = {Integer.MIN_VALUE, Integer.MAX_VALUE};
        int curMax = Integer.MIN_VALUE;
        int diff = Integer.MAX_VALUE;

        Queue<Node> pq = new PriorityQueue<>((a, b) -> {
            return nums.get(a.row).get(a.col) - nums.get(b.row).get(b.col);
        });
        for (int r = 0; r < nums.size(); r++) {
            if (!nums.get(r).isEmpty()) {
                curMax = Math.max(curMax, nums.get(r).get(0));
                pq.offer(new Node(r, 0));
            }
        }
        diff = curMax - nums.get(pq.peek().row).get(pq.peek().col);
        res[0] = nums.get(pq.peek().row).get(pq.peek().col);
        res[1] = curMax;

        while (pq.peek().col+1 < nums.get(pq.peek().row).size()) {
            Node pollNode = pq.poll();
            pollNode.col += 1;
            curMax = Math.max(curMax, nums.get(pollNode.row).get(pollNode.col));
            pq.offer(pollNode);
            int newDiff = curMax - nums.get(pq.peek().row).get(pq.peek().col);
            if (newDiff < diff) {
                diff = newDiff;
                res[0] = nums.get(pq.peek().row).get(pq.peek().col);;
                res[1] = curMax;
            }
        }

        return res;
    }
}

0/1 Knapsack (Dynamic Programming)

0/1 Knapsack

Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays val[0..n-1] and weight[0..n-1] which represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the maximum value subset of val[] such that sum of the weights of this subset is smaller than or equal to W. You cannot break an item, either pick the complete item, or don’t pick it (0-1 property).

Source: 0-1 Knapsack Problem DP-10

Explanation

I had written a post about Knapsack Problem which is explained in detail.
Dynamic Programming is an algorithmic paradigm that solves a given complex problem by breaking it into subproblems and stores the results of subproblems to avoid computing the same results again. Following are the two main properties of a problem that suggests that the given problem can be solved using Dynamic programming.
1. Overlapping Subproblems
2. Optimal Substructure
Overlapping Subproblems: Dynamic Programming is mainly used when solutions of same subproblems are needed again and again. In dynamic programming, computed solutions to subproblems are stored in a table so that these don’t have to be recomputed.

Optimal Substructure: A given problems has Optimal Substructure Property if optimal solution of the given problem can be obtained by using optimal solutions of its subproblems.
We can use dynamic programming to solve this problem. We create a 2 dimensional array dp[i][j] which represents the the maximum value we can make by putting the first i item in a knapsack with j capacity. We have:
- dp[i][0] = dp[0][j] = 0
- dp[i][j] = dp[i-1][j] if weight[i] > j
- dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i]] + val[i]) if j >= weight[i]

Source:

Overlapping Subproblems Property in Dynamic Programming DP-1

Optimal Substructure Property in Dynamic Programming DP-2

Solution

public class Main {
    public static void main(String[] args) {
        int[] weight = { 3, 5, 2, 6, 4 };
        int[] val = { 4, 4, 3, 5, 3 };
        int W = 12;
        int n = val.length;

        int[][] dp = new int[n + 1][W + 1];
        int[][] path = new int[n + 1][W + 1];
        // intialize the first row and column
        // no need to fill full the knapsack
        for (int i = 0; i < dp[0].length; i++) {
            dp[0][i] = 0;
        }
        for (int i = 0; i < dp.length; i++) {
            dp[i][0] = 0;
        }
        // dynamic function
        for (int i = 1; i < dp.length; i++) {
            for (int j = 1; j < dp[0].length; j++) {
                if (weight[i - 1] > j)
                    dp[i][j] = dp[i - 1][j];
                else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + val[i - 1]);
                }
            }
        }

        // stores the result of Knapsack
        int res = dp[n][W];
        System.out.println("Maximum value " + res);

        int w = W;
        // check if the last row has the same result
        for (int i = n; i > 0 && res > 0; i--) {
            if (dp[i - 1][w] == res)
                continue;
            else {
                System.out.println("Choose the " + i + "th item.");
                res = res - val[i - 1];
                w = w - weight[i - 1];
            }
        }
    }
}

// Output:
// Maximum value 12
// Choose the 4th item.
// Choose the 3th item.
// Choose the 1th item.

LeetCode 416. Partition Equal Subset Sum

Given a non-empty array containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Note:

Each of the array element will not exceed 100.
The array size will not exceed 200.

Example 1:

Input: [1, 5, 11, 5]

Output: true

Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

Input: [1, 2, 3, 5]

Output: false

Explanation: The array cannot be partitioned into equal sum subsets.

Explanation

This problem is asking for all the numbers in the array, can any of these numbers form the sum sum / 2. This is a 0-1 knapsack problem. Dynamic state is boolean[][] dp[i][j] and it represents for the first i numbers, they can form the sum j or not.
Dynamic init is first row are false, dp[0][c] = false where c != 0 because for the first 0 number, we cannot form any sum. dp[r][0] = true because if the sum is 0, then for the first any number we can always form the sum 0.
Dynamic function. For every number, we either choose it to form the sum j or not choose it. If we don’t choose the current number, then we have dp[r][c] = dp[r-1][c]. If we choose the current number, then we have dp[r][c] = dp[r-1][c-curNum] where curNum = nums[r-1].
Dynamic result is dp[nums.length][sum / 2].

Solution

class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num: nums) sum += num;
        if (sum % 2 != 0) return false;
        int target = sum / 2;

        boolean[][] dp = new boolean[nums.length + 1][target + 1];
        for (int c = 0; c < dp[0].length; c++) {
            dp[0][c] = false;
        }
        for (int r = 0; r < dp.length; r++) {
            dp[r][0] = true;
        }

        for (int r = 1; r < dp.length; r++) {
            for (int c = 1; c < dp[0].length; c++) {
                dp[r][c] = dp[r-1][c];
                if (nums[r-1] <= c) {
                    dp[r][c] = dp[r][c] || dp[r-1][c-nums[r-1]];
                }
            }
        }

        return dp[nums.length][target];
    }
}

// class Solution {
//     public boolean canPartition(int[] nums) {
//         int sum = 0;
//         for (int num: nums) sum += num;
//         if (sum % 2 != 0) return false;
//         int target = sum / 2;

//         boolean[] dp = new boolean[target + 1];
//         dp[0] = true;

//         for (int num: nums) {
//             for (int j = dp.length-1; j >= 0; j--) {
//                 if (j - num >= 0) dp[j] = dp[j] || dp[j-num];
//             }
//         }

//         return dp[target];
//     }
// }

Subset Sum

Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.

Example

Input:  nums[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output:  True  //There is a subset (4, 5) with sum 9.

Source:

Subset Sum Problem DP-25

Perfect Sum Problem (Print all subsets with given sum)

Explanation

Same as Partition Equal Subset Sum, we can create a two dimensional array dp[i][j] which represents for the first i number, if any of them can form the sum j. At the end, we will return dp[nums.length][sum].

Solution

class Main {
    static boolean canPartition(int[] nums, int sum) {
        boolean[] dp = new boolean[sum + 1];
        dp[0] = true;

        for (int num: nums) {
            for (int i = dp.length-1; i >= 0; i--) {
                if (i - num >= 0) dp[i] = dp[i] || dp[i-num];
            }
        }

        return dp[sum];
    }

    public static void main (String[] args) {
        int[] nums = {3, 34, 4, 12, 5, 2};
        int sum = 9;
        System.out.println(canPartition(nums, sum));
    }
}

// Output:
// true

Minimum Subset Sum Difference

Given a set of positive integers, write a function to divide it into two sets S1 and S2 such that the absolute difference between their sums is minimum.

If there is a set S with n elements, then if we assume Subset1 has m elements, Subset2 must have n-m elements and the value of abs(sum(Subset1) – sum(Subset2)) should be minimum.

Example 1:

Input: nums = [1, 6, 11, 5]
Output: 1
Explanation:
Subset1 = [1, 5, 6], sum of Subset1 = 12
Subset2 = [11], sum of Subset2 = 11
abs(11 - 12) = 1

Example 2:

Input: nums = [1, 2, 3, 4]
Output: 0
Explanation:
Subset1 = [1, 4], sum of Subset1 = 5
Subset2 = [2, 3], sum of Subset2 = 5
abs(5 - 5) = 0

Source: 724. Minimum Partition

Explanation

Since we want the difference between S1’s sum and S2’s sum be minimum, then S1’s sum and S2’s sum should be closed to equal. In other words, S1’s sum and S2’s sum should be closed to totalSum / 2.
For all the elements of the array, loop from i = totalSum / 2 down to i = 1, can we find a subset sum equal to i. If we can find the subset sum equal to i, then we have S1’s sum be i and S2’s sum be totalSum - i. Their difference will be totalSum - i - i.

Solution

public class Solution {
    // public int findMin(int[] nums) {
    //     int sum = 0;
    //     for (int num: nums) {
    //         sum += num;
    //     }
    //     boolean[][] dp = new boolean[nums.length + 1][sum / 2 + 1];
    //     for (int c = 0; c < dp[0].length; c++) {
    //         dp[0][c] = false;
    //     }
    //     for (int r = 0; r < dp.length; r++) {
    //         dp[r][0] = true;
    //     }

    //     for (int r = 1; r < dp.length; r++) {
    //         for (int c = 1; c < dp[0].length; c++) {
    //             dp[r][c] = dp[r-1][c];
    //             if (c - nums[r-1] >= 0) dp[r][c] = dp[r][c] || dp[r-1][c - nums[r-1]];
    //         }
    //     }

    //     int diff = -1;
    //     for (int i = sum / 2; i >= 0; i--) {
    //         if (dp[nums.length][i]) {
    //             diff = sum - i - i;
    //             break;
    //         }
    //     }

    //     return diff;
    // }

    public int findMin(int[] nums) {
        int sum = 0;
        for (int num: nums) {
            sum += num;
        }
        boolean[] dp = new boolean[sum / 2 + 1];
        dp[0] = true;

        for (int num: nums) {
            for (int i = dp.length - 1; i >= 0; i--) {
                if (i - num >= 0) dp[i] = dp[i] || dp[i - num];
            }
        }

        int diff = -1;
        for (int i = dp.length - 1; i >= 0; i--) {
            if (dp[i]) {
                diff = sum - i - i;
                break;
            }
        }

        return diff;
    }
}

Perfect Sum Problem (Print all subsets with given sum)

Given an array of integers and a sum, the task is to print all subsets of given array with sum equal to given sum.

Example

Input : arr[] = {2, 3, 5, 6, 8, 10}
        sum = 10
Output : 5 2 3
         2 8
         10

Input : arr[] = {1, 2, 3, 4, 5}
        sum = 10
Output : 4 3 2 1
         5 3 2
         5 4 1

Source: Perfect Sum Problem (Print all subsets with given sum)

Explanation

First, we need to build the 2 dimensional dp table using the bottom up method. Then we will use backtracking method to print all the subsets. In the backtracking helper method, we will pass the dp table, the target sum, the current index (we will start from the last index back to the first index and we will start from the bottom right cornor), the result list, the sub list, and the nums array.
In the backtracking method, the base case is if the sum is equals to 0, then we add the current list to the result list. If the index is less than 0, or the target sum is less than 0, then we return.
After checking the base case, if the dp[index][target] is true, then it means we can form the target using numbers between nums[0] to nums[index] inclusive. If dp[index][target] is false, then we return out since it can’t form the target. So when it’s true, we only consider two cases. Either include nums[index] in the subset or not. In other words, when not include, it’s recursively calling the helper method with index - 1, and other parameters are the same. If we include, we add nums[index] to the sublist, then recursively calling the helper method with target = target - nums[index] and index = index - 1. Next we also need to backtrack to remove the last added element from the sublist.

Solution

class Solution {
    void helper(boolean[][] dp, int target, int idx, List<List<Integer>> res, List<Integer> cur, int[] nums) {
        if (target == 0) {
            res.add(new ArrayList<>(cur));
            return;
        }
        if (idx < 0 || target < 0) return;
        if (dp[idx][target]) {
            helper(dp, target, idx-1, res, cur, nums);
            cur.add(nums[idx]);
            helper(dp, target-nums[idx], idx-1, res, cur, nums);
            cur.remove(cur.size()-1);
        }
    }

    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int num: nums) sum += num;
        if (sum % 2 != 0) return false;
        int target = sum / 2;
        boolean[][] dp = new boolean[nums.length][target + 1];

        for (int r = 0; r < dp.length; r++) {
            dp[r][0] = true;
        }
        for (int c = 1; c < dp[0].length; c++) {
            if (nums[0] == c) dp[0][c] = true;
        }

        for (int r = 1; r < dp.length; r++) {
            for (int c = 1; c < dp[0].length; c++) {
                dp[r][c] = dp[r-1][c];
                if (nums[r] <= c) {
                    dp[r][c] = dp[r][c] || dp[r-1][c - nums[r]];
                }
            }
        }

        // return dp[nums.length-1][target];
        if (!dp[nums.length-1][target]) return false;

        List<List<Integer>> res = new ArrayList<>();
        List<Integer> cur = new ArrayList<>();
        helper(dp, target, dp.length-1, res, cur, nums);
        System.out.println(res);
        return true;
    }
}

LeetCode 494. Target Sum

You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

Input: nums is [1, 1, 1, 1, 1], S is 3.
Output: 5
Explanation:

-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

Note:

The length of the given array is positive and will not exceed 20.
The sum of elements in the given array will not exceed 1000.
Your output answer is guaranteed to be fitted in a 32-bit integer.

Explanation 1

This problem asks us to find the sum of all elements (we can make these elements positive or negative) equals to S. We can use recursion to solve this problem. First, think about if we plus the first number nums[i], then the rest of the number should sum up to S-nums[i]. So, it’s the same problem as the original problem. So now the S becomes S-nums[i], the first number becomes nums[i+1]. The base case is if i == nums.length, then at means we already try all elements, so we check if S == 0 then we increase res. Similarlly, if we minus the first number, then the rest of the number should equals to S + nums[i].

Solution 1

class Solution {
    int res = 0;

    void helper(int[] nums, int S, int start) {
        if (start == nums.length) {
            if (S == 0) {
                res += 1;
            }
            return;
        }
        helper(nums, S-nums[start], start+1);
        helper(nums, S+nums[start], start+1);
    }

    public int findTargetSumWays(int[] nums, int S) {
        helper(nums, S, 0);
        return res;
    }
}

Explanation 2

We can optimize the runtime for solution1. Starting at index start, we can record how many ways to form a sum S1 and S2, etc. So we need to create an array of HashMap, dp[start] is a HashMap, the key is the sum, the value is the number of ways to form that sum.
The helper function will return an int. The base case is when start == nums.length, we check if S equals to 0. If it is, then we return 1, else return 0. Same as explanation1, we have two cases, either plus the first number or minus the first number, so dp[start].get(S) will equals to the sum of recursive result of both cases.

Solution 2

class Solution {
    int helper(int[] nums, int S, int start, Map<Integer, Integer>[] dp) {
        if (start == nums.length) {
            if (S == 0) {
                return 1;
            } else {
                return 0;
            }
        }
        if (dp[start].containsKey(S)) {
            return dp[start].get(S);
        }
        int cnt1 = helper(nums, S-nums[start], start+1, dp);
        int cnt2 = helper(nums, S+nums[start], start+1, dp);
        dp[start].put(S, cnt1+cnt2);
        return dp[start].get(S);
    }

    public int findTargetSumWays(int[] nums, int S) {
        Map<Integer, Integer>[] dp = new HashMap[nums.length];
        for (int i = 0; i < dp.length; i++) {
            dp[i] = new HashMap<Integer, Integer>();
        }
        return helper(nums, S, 0, dp);
    }
}

Explanation 3

The recursive solution is very slow, because its runtime is exponential.

The original problem statement is equivalent to:

Find a subset of nums that need to be positive, and the rest of them negative, such that the sum is equal to target.

Let P be the positive subset and N be the negative subset. For example:

Given nums = [1, 2, 3, 4, 5] and target = 3 then one possible solution is +1-2+3-4+5 = 3.

Here positive subset is P = [1, 3, 5] and negative subset is N = [2, 4]

Then let’s see how this can be converted to a subset sum problem:

```
                  sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)
                       2 * sum(P) = target + sum(nums)
```

So the original problem has been converted to a subset sum problem as follows:

Find a subset P of nums such that sum(P) = (target + sum(nums)) / 2

Note that the above formula has proved that target + sum(nums) must be even.

We can use that fact to quickly identify inputs that do not have a solution.

Solution 3

class Solution {
    int subsetSum(int[] nums, int target) {
        int[] dp = new int[target+1];
        dp[0] = 1;
        for (int num: nums) {
            for (int i = target; i >= num; i--) {
                dp[i] += dp[i-num];
            }
        }
        return dp[target];
    }

    public int findTargetSumWays(int[] nums, int S) {
        int sum = 0;
        for (int num: nums) sum += num;
        return sum < S || (S + sum) % 2 != 0 ? 0: subsetSum(nums, (S + sum)/2);
    }
}

Topological Sort (Graph)

Topological Sort

Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u->v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.

For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 0 3 1”. The first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no incoming edges). One example for Topological Sort is build dependency problem. If dependencyA depends on dependencyB and dependencyC, then dependencyA can be resolved anytime after dependencyB and dependencyC are resolved.

Topological Sorting vs Depth First Traversal (DFS):

For example, in the given graph, the vertex ‘5’ should be printed before vertex ‘0’, but unlike DFS, in topological sort, the vertex ‘4’ should also be printed before vertex ‘0’. So Topological sorting is different from DFS. For example, a DFS of the shown graph is “5 2 3 1 0 4”, but it is not a topological sorting.

Source: Topological Sorting

Explanation 1

I had written a post about Topological Sort which is explained in detail.
Using queue method. First, we need to have an adjacent list. For example adjancentList[v] = {a, b, c} means before we visit a or b or c, we first visit v. Then we update every vertex’s number of inDegree or dependencies. For example, inDegree[a] = 1 means before we visit vertex a, we need to visit 1 other vertex.
Next, we push all vertex that has 0 dependencies to the queue. While the queue is not empty, we poll the current vertex out and add to the result list. Then we subtract 1 of the inDegree for every vertex in the poll vertex’s adjancentList. For example, if we poll the v out, then we update inDegree[a] -= 1, inDegree[b] -= 1 and inDegree[c] -= 1. After updating, if any of these vertex has 0 indegree, we push it to the queue.
Outside of the queue, if the result list has the same size as the number of vertex, then we return the result list.

Solution 1

import java.util.*;

class Graph {
    private int numVertices; // Number of vertices
    private List<Integer>[] adjLst; // Adjacency List

    // Constructor
    Graph(int n) {
        numVertices = n;
        adjLst = new LinkedList[numVertices];
        for (int i = 0; i < numVertices; ++i) {
            adjLst[i] = new LinkedList<>();
        }
    }

    public void addEdge(int u, int v) {
        adjLst[u].add(v);
    }

    public int getNumVertices() {
        return numVertices;
    }

    public List<Integer>[] getAdj() {
        return this.adjLst;
    }
}

public class Main {
    public static List<Integer> topologicalSort(Graph g) {
        List<Integer> res = new ArrayList<>();

        int numVertices = g.getNumVertices();
        int[] inDegree = new int[numVertices];

        List<Integer>[] adjacencyList = g.getAdj();
        for (List<Integer> lst : adjacencyList) {
            for (int v : lst) {
                inDegree[v]++;
            }
        }

        Queue<Integer> queue = new LinkedList<>();

        // start from nodes with in degree 0
        for (int i = 0; i < numVertices; i++) {
            if (inDegree[i] == 0)
                queue.offer(i);
        }

        while (!queue.isEmpty()) {
            int curr = queue.poll();
            res.add(curr);
            for (int child : adjacencyList[curr]) {
                inDegree[child]--;
                if (inDegree[child] == 0) {
                    queue.offer(child);
                }
            }
        }

        return res.size() == numVertices ? res : new ArrayList<>();
    }

    public static void main(String args[]) {
        Graph g = new Graph(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);

        List<Integer> res = topologicalSort(g);
        System.out.println(res.toString());
    }
}

// Output:
// [4, 5, 2, 0, 3, 1]

Explanation 2

We can also use stack method to solve this problem.
Loop through every vertex, if the iterated vertex is not visited, then we pass it to the recursively helper method.
In the helper method, we first mark the current vertex as visited. Then we loop through its adjacent vertices and call these adjacent vertices with the helper method. Outside of the this loop, we push the vertex to the stack. In other words, a vertex is pushed to stack only when all of its adjacent vertices (and their adjacent vertices and so on) are already in stack.
In the main method, we print the stack from top to bottom.

Solution 2

import java.util.*;

class Graph {
    private int numVertices; // Number of vertices
    private List<Integer>[] adjLst; // Adjacency List

    // Constructor
    Graph(int n) {
        numVertices = n;
        adjLst = new LinkedList[numVertices];
        for (int i = 0; i < numVertices; ++i) {
            adjLst[i] = new LinkedList<>();
        }
    }

    public void addEdge(int u, int v) {
        adjLst[u].add(v);
    }

    public int getNumVertices() {
        return numVertices;
    }

    public List<Integer>[] getAdj() {
        return this.adjLst;
    }
}

public class Main {
    private static void helper(int u, Stack<Integer> stack, Set<Integer> visited, List<Integer>[] adjLst) {
        visited.add(u);
        for (int v : adjLst[u]) {
            if (visited.contains(v)) {
                continue;
            }
            helper(v, stack, visited, adjLst);
        }
        stack.push(u);
    }

    public static List<Integer> topologicalSort(Graph graph) {
        Stack<Integer> stack = new Stack<>();
        Set<Integer> visited = new HashSet<>();
        List<Integer>[] adjLst = graph.getAdj();
        int numVertices = graph.getNumVertices();

        for (int u = 0; u < numVertices; u++) {
            if (visited.contains(u)) {
                continue;
            }
            helper(u, stack, visited, adjLst);
        }

        List<Integer> res = new ArrayList<>();
        while (!stack.isEmpty()) {
            res.add(stack.pop());
        }

        return res.size() == numVertices ? res : new ArrayList<>();
    }

    public static void main(String args[]) {
        Graph g = new Graph(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);

        List<Integer> res = topologicalSort(g);
        System.out.println(res.toString());
    }
}

// Output:
// [5, 4, 2, 3, 1, 0]

LeetCode 207. Course Schedule

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

Example 1:

Input: 2, [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
             To take course 1 you should have finished course 0. So it is possible.

Example 2:

Input: 2, [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
             To take course 1 you should have finished course 0, and to take course 0 you should
             also have finished course 1. So it is impossible.

Note:

The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
You may assume that there are no duplicate edges in the input prerequisites.

Explanation 1

First, we need to build an adjancent list and the inDegree array.
Push all the courses that have inDegree 0, in other words, the courses that have no prerequisite to the queue. While the queue is not empty, we poll the course out and increae the counter, update the indegree of its adjancent list’s courses. If any of these updated course has inDegree 0, we push it to the queue.
Outside the queue, we check if the counter is equal to the number of courses. If the counter is equal to the number of courses, that means we can visit all the courses, so we return true, else return false.

Solution 1

class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<Integer>[] adjancentList = new List[numCourses];
        for (int i = 0; i < adjancentList.length; i++) {
            adjancentList[i] = new ArrayList<>();
        }

        int[] inDegree = new int[numCourses];
        for (int[] prereq: prerequisites) {
            adjancentList[prereq[1]].add(prereq[0]);
            inDegree[prereq[0]] += 1;
        }

        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < inDegree.length; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        int cnt = 0;
        while (!queue.isEmpty()) {
            int pollCourse = queue.poll();
            cnt += 1;
            for (int a: adjancentList[pollCourse]) {
                inDegree[a] -= 1;
                if (inDegree[a] == 0) {
                    queue.offer(a);
                }
            }
        }

        return cnt == numCourses;
    }
}

Explanation 2

We can also use DFS to solve this problem. First, we make a directed graph as above. Also, we need to make a one dimensional array visit[] which is used to record if the class i is visited or not. We use 0 as unvisit, 1 as visit, -1 as conflict. Since we use DFS, we can think of checking the classes linearly, if these classes make a circle, then it’s conflict and we return false.
We loop through all the classes, for each class, we think of it as a starting point and use the helper function to check it.
In the helper function, before we DFS into the deeper class, we mark the class in the visit array -1. So the base case is if the class is already mark as -1, then it means we make a circle, and we immediatly return false. After checking all the classes in index i, in other word, sublist of graph[i], we mark class i as visit 1. So the base case add one more condition, if visit[i] is 1, then we immediately return true since we confirm that base on starting point class i, all its advanced class do not make a circle.

Solution 2

class Solution {
    boolean helper(List<Integer>[] graph, int[] visit, int i) {
        if (visit[i] == 1) return true;
        if (visit[i] == -1) return false;
        visit[i] = -1;
        for (int a: graph[i]) {
            if (!helper(graph, visit, a)) return false;
        }
        visit[i] = 1;
        return true;
    }

    public boolean canFinish(int numCourses, int[][] prerequisites) {
        List<Integer>[] graph = new ArrayList[numCourses];
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] pair: prerequisites) {
            graph[pair[1]].add(pair[0]);
        }

        int[] visit = new int[numCourses];
        for (int i = 0; i < numCourses; i++) {
            if (!helper(graph, visit, i)) return false;
        }

        return true;
    }
}

LeetCode 210. Course Schedule II

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, return the ordering of courses you should take to finish all courses.

There may be multiple correct orders, you just need to return one of them. If it is impossible to finish all courses, return an empty array.

Example 1:

Input: 2, [[1,0]]
Output: [0,1]
Explanation: There are a total of 2 courses to take. To take course 1 you should have finished
             course 0. So the correct course order is [0,1] .

Example 2:

Input: 4, [[1,0],[2,0],[3,1],[3,2]]
Output: [0,1,2,3] or [0,2,1,3]
Explanation: There are a total of 4 courses to take. To take course 3 you should have finished both
             courses 1 and 2. Both courses 1 and 2 should be taken after you finished course 0.
             So one correct course order is [0,1,2,3]. Another correct ordering is [0,2,1,3] .

Note:

The input prerequisites is a graph represented by a list of edges, not adjacency matrices. Read more about how a graph is represented.
You may assume that there are no duplicate edges in the input prerequisites.

Explanation 1

Using the same queue method as LeetCode 207. Course Schedule, all we need to do is create a result array. When we poll the course out of the queue, we add it to the result array. At the end, if the counter is equal to the number of courses, then we return the result array.

Solution 1

class Solution {
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int[] res = new int[numCourses];
        List<Integer>[] adjancentList = new List[numCourses];
        for (int i = 0; i < adjancentList.length; i++) {
            adjancentList[i] = new ArrayList<>();
        }

        int[] inDegree = new int[numCourses];
        for (int[] prereq: prerequisites) {
            adjancentList[prereq[1]].add(prereq[0]);
            inDegree[prereq[0]] += 1;
        }

        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < inDegree.length; i++) {
            if (inDegree[i] == 0) {
                queue.offer(i);
            }
        }

        int cnt = 0;
        while (!queue.isEmpty()) {
            int pollCourse = queue.poll();
            res[cnt++] = pollCourse;
            for (int a: adjancentList[pollCourse]) {
                inDegree[a] -= 1;
                if (inDegree[a] == 0) {
                    queue.offer(a);
                }
            }
        }

        return cnt == numCourses ? res : new int[0];
    }
}

Explanation 2

Using the same stack method as LeetCode 207. Course Schedule, all we need to do is creating a stack and pass it to the helper method. After we visited[curCourse] = 1, we then push the curCourse to the stack.
At the end, we pop the stack and add the pop course to the result array.

Solution 2

class Solution {
    boolean helper(List<Integer>[] graph, int[] visit, int i, Stack<Integer> st) {
        if (visit[i] == 1) return true;
        if (visit[i] == -1) return false;
        visit[i] = -1;
        for (int a: graph[i]) {
            if (!helper(graph, visit, a, st)) return false;
        }
        visit[i] = 1;
        st.push(i);
        return true;
    }

    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int[] res = new int[numCourses];
        List<Integer>[] graph = new ArrayList[numCourses];
        for (int i = 0; i < numCourses; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] pair: prerequisites) {
            graph[pair[1]].add(pair[0]);
        }

        int[] visit = new int[numCourses];
        Stack<Integer> st = new Stack<>();
        for (int i = 0; i < numCourses; i++) {
            if (!helper(graph, visit, i, st)) return new int[0];
        }

        int idx = 0;
        while(!st.isEmpty()) {
            res[idx++] = st.pop();
        }
        return res;
    }
}

All Tasks Scheduling Orders

Given a Directed Acyclic Graph (DAG), print all topological sorts of the graph.

Example:

All topological sorts of the given graph are:

5 0 2 3 1
5 2 0 3 1
5 2 3 0 1
5 2 3 1 0
2 3 4 0 1
2 3 4 1 0
2 4 0 3 1
2 4 3 0 1
2 4 3 1 0
4 0 2 3 1
4 2 0 3 1
4 2 3 0 1
4 2 3 1 0

Explanation

We can use backtracking method to print all the paths. First, we build the adjancent list and the inDegree list. Then we call a helper method by passing the graph, the number of vertexes, the visited array, and the list of path.
In the helper method, we loop through all the vertexes, if the current vertex has inDegree 0 and it’s not visited, then we add it to the path and mark it as visited. Also we loop through its adjancent vertexes and update their inDegree subtract 1. Then we recursively call the helper method. After calling the recursive helper method, we need to backtrack. So we restore the current vertex’s adjancent vertexes’ inDegree plus 1, remove the current vertex from the path list, and mark it as not visited.
In the helper method, after looping through all the vertexes, if the path list has size N, then we print the path list.

Solution

import java.util.*;

class Edge {
    int source, dest;
    public Edge(int source, int dest) {
        this.source = source;
        this.dest = dest;
    }
};

class Graph {
    List<List<Integer>> adjList = null;
    List<Integer> indegree = null;

    Graph(List<Edge> edges, int N) {
        adjList = new ArrayList<>(N);
        for (int i = 0; i < N; i++) {
            adjList.add(i, new ArrayList<>());
        }

        indegree = new ArrayList<>(Collections.nCopies(N, 0));

        for (int i = 0; i < edges.size(); i++) {
            int src = edges.get(i).source;
            int dest = edges.get(i).dest;

            adjList.get(src).add(dest);
            indegree.set(dest, indegree.get(dest) + 1);
        }
    }
}

class Main {
    public static void findAllTopologicalOrders(Graph graph, List<Integer> path,
                                                boolean[] discovered, int N) {
        for (int v = 0; v < N; v++) {
            if (graph.indegree.get(v) == 0 && !discovered[v]) {
                for (int u: graph.adjList.get(v)) {
                    graph.indegree.set(u, graph.indegree.get(u) - 1);
                }
                path.add(v);
                discovered[v] = true;

                findAllTopologicalOrders(graph, path, discovered, N);

                for (int u: graph.adjList.get(v)) {
                    graph.indegree.set(u, graph.indegree.get(u) + 1);
                }
                path.remove(path.size() - 1);
                discovered[v] = false;
            }
        }

        if (path.size() == N) {
            System.out.println(path);
        }
    }

    public static void printAllTopologicalOrders(Graph graph) {
        int N = graph.adjList.size();
        boolean[] discovered = new boolean[N];
        List<Integer> path = new ArrayList<>();
        findAllTopologicalOrders(graph, path, discovered, N);
    }

    public static void main(String[] args) {
        List<Edge> edges = Arrays.asList(
                                new Edge(5, 2), new Edge(5, 0),
                                new Edge(4, 0), new Edge(4, 1),
                                new Edge(2, 3), new Edge(3, 1)
                            );
        int N = 6;
        Graph graph = new Graph(edges, N);
        printAllTopologicalOrders(graph);
    }
}

// Output:
// [4, 5, 0, 2, 3, 1]
// [4, 5, 2, 0, 3, 1]
// [4, 5, 2, 3, 0, 1]
// [4, 5, 2, 3, 1, 0]
// [5, 2, 3, 4, 0, 1]
// [5, 2, 3, 4, 1, 0]
// [5, 2, 4, 0, 3, 1]
// [5, 2, 4, 3, 0, 1]
// [5, 2, 4, 3, 1, 0]
// [5, 4, 0, 2, 3, 1]
// [5, 4, 2, 0, 3, 1]
// [5, 4, 2, 3, 0, 1]
// [5, 4, 2, 3, 1, 0]

Source:

All Topological Sorts of a Directed Acyclic Graph

Find all Possible Topological Orderings of a DAG

LeetCode 269. Alien Dictionary

There is a new alien language which uses the latin alphabet. However, the order among letters are unknown to you. You receive a list of non-empty words from the dictionary, where words are sorted lexicographically by the rules of this new language. Derive the order of letters in this language.

Example 1:

Input:
[
  "wrt",
  "wrf",
  "er",
  "ett",
  "rftt"
]

Output: "wertf"

Example 2:

Input:
[
  "z",
  "x"
]

Output: "zx"

Example 3:

Input:
[
  "z",
  "x",
  "z"
]

Output: ""

Explanation: The order is invalid, so return "".

Note:

You may assume all letters are in lowercase.
You may assume that if a is a prefix of b, then a must appear before b in the given dictionary.
If the order is invalid, return an empty string.
There may be multiple valid order of letters, return any one of them is fine.

Explanation

We can use Topological Sort to solve this problem. First, we need to build the adjancent list array and the inDegree array. How do we know the dependencies? We can loop through the input list, and each time we compare the current iterated word words[i] with its next word words[i + 1]. For example, by comparing wrt and wrf, if the character is different, then we have the dependencies that t is before f.

Solution

class Solution {
    public String alienOrder(String[] words) {
        if (words.length == 1) {
            char[] arr = words[0].toCharArray();
            Arrays.sort(arr);
            return new String(arr);
        }

        List<Character>[] adjLst = new List[26];
        for (int i = 0; i < adjLst.length; i++) {
            adjLst[i] = new ArrayList<>();
        }
        int[] inDegree = new int[26];
        Arrays.fill(inDegree, -1);
        for (int i = 0; i < words.length - 1; i++) {
            char[] wordA = words[i].toCharArray();
            char[] wordB = words[i + 1].toCharArray();
            for (char c: wordA) {
                if (inDegree[c - 'a'] == -1) inDegree[c - 'a'] = 0;
            }
            for (char c: wordB) {
                if (inDegree[c - 'a'] == -1) inDegree[c - 'a'] = 0;
            }
            int minLen = wordA.length;
            if (wordB.length < minLen) minLen = wordB.length;
            for (int j = 0; j < minLen; j++) {
                if (wordA[j] != wordB[j]) {
                    adjLst[wordA[j] - 'a'].add(wordB[j]);
                    inDegree[wordB[j] - 'a'] += 1;
                    break;
                }
            }
        }
        Queue<Character> queue = new LinkedList<>();
        for (int i = 0; i < inDegree.length; i++) {
            if (inDegree[i] == 0) queue.offer((char) ('a' + i));
        }

        StringBuilder sb = new StringBuilder();
        int cnt = 0;
        while (!queue.isEmpty()) {
            Character pollCh = queue.poll();
            cnt += 1;
            sb.append(pollCh);
            for (Character ch: adjLst[pollCh - 'a']) {
                inDegree[ch - 'a'] -= 1;
                if (inDegree[ch - 'a'] == 0) {
                    queue.offer(ch);
                }
            }
        }

        int numUnused = 0;
        for (int i = 0; i < inDegree.length; i++) {
            if (inDegree[i] == -1) numUnused += 1;
        }

        return 26 - numUnused == cnt ? sb.toString() : "";
    }
}

Miscellaneous

LeetCode 668. Kth Smallest Number in Multiplication Table

Nearly every one have used the Multiplication Table. But could you find out the k-th smallest number quickly from the multiplication table?

Given the height m and the length n of a m * n Multiplication Table, and a positive integer k, you need to return the k-th smallest number in this table.

Example 1:

Input: m = 3, n = 3, k = 5
Output:
Explanation:
The Multiplication Table:
1   2   3
2   4   6
3   6   9

The 5-th smallest number is 3 (1, 2, 2, 3, 3).

Example 2:

Input: m = 2, n = 3, k = 6
Output:
Explanation:
The Multiplication Table:
1   2   3
2   4   6

The 6-th smallest number is 6 (1, 2, 2, 3, 4, 6).

Note:

The m and n will be in the range [1, 30000].
The k will be in the range [1, m * n]

Explanation

Similar to Kth Smallest Number in a Sorted Matrix, we can use binary search method to solve this problem. The range will be 1 to m * n.
First, we know the smallest number left is 1, the larget number right is m * n. While left < right, we can calculate the mid. Next, we want to calculate how many numbers less than or equal to mid and let say it’s called cnt.
We can compare mid with the bottom left number, and we use i=m, j=1 to define the position of the bottom left number’s row and column. If the bottom left number is less than or equal to mid, then we move the bottom left number to the right, in other word, j += 1, and update numLessEqualMid += i. Else we move the bottom left number 1 row up, which is i -= 1. Repeat this process while i >= 1 && j <= n.
If cnt is less than k, then we need to update left = mid + 1, else we update right = mid. Repeat this process while left < right.
Outside of the while loop when left is right are equal, we can just return left as our answer.

Solution

class Solution {
    public int findKthNumber(int m, int n, int k) {
        int left = 1, right = m * n;
        while (left < right) {
            int mid = left + (right - left) / 2;
            int cnt = 0, i = m, j = 1;
            while (i >= 1 && j <= n) {
                if (i * j <= mid) {
                    cnt += i;
                    j += 1;
                } else {
                    i -= 1;
                }
            }
            if (cnt < k) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }

        return left;
    }
}