September LeetCoding Challenge

Posted on | In

Last month I got an email said would go back to office to work after labor day, not sure if will postpone or not because originaly said go back to office in July, then postponed to August, now is September. Anyway, Let’s continue September LeetCoding Challenge.

Week 1: September 1st - September 7th

Read N Characters Given Read4

Given a file and assume that you can only read the file using a given method read4, implement a method to read n characters.

Method read4:

The API read4 reads 4 consecutive characters from the file, then writes those characters into the buffer array buf.

The return value is the number of actual characters read.

Note that read4() has its own file pointer, much like FILE *fp in C.

Definition of read4:

1
2
3
4
    Parameter:  char[] buf4
    Returns:    int

Note: buf4[] is destination not source, the results from read4 will be copied to buf4[]

Below is a high level example of how read4 works:

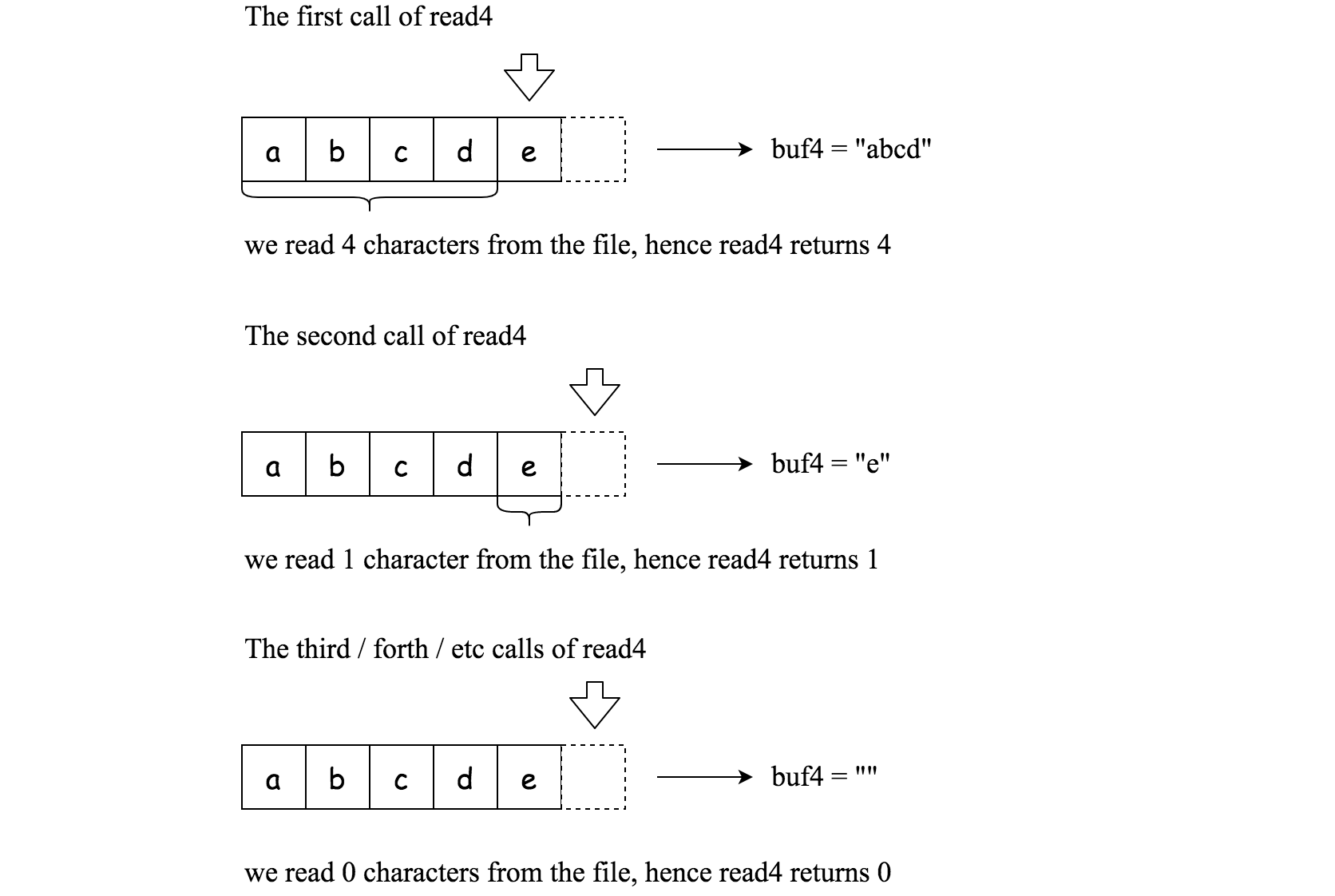
Read N Characters Given Read4

1
2
3
4
5
File file("abcde"); // File is "abcde", initially file pointer (fp) points to 'a'
char[] buf4 = new char[4]; // Create buffer with enough space to store characters
read4(buf4); // read4 returns 4. Now buf = "abcd", fp points to 'e'
read4(buf4); // read4 returns 1. Now buf = "e", fp points to end of file
read4(buf4); // read4 returns 0. Now buf = "", fp points to end of file

Method read:

By using the read4 method, implement the method read that reads n characters from the file and store it in the buffer array buf. Consider that you cannot manipulate the file directly.

The return value is the number of actual characters read.

Definition of read:

1
2
3
4
    Parameters: char[] buf, int n
    Returns:    int

Note: buf[] is destination not source, you will need to write the results to buf[]

Example 1:

1
2
3
Input: file = "abc", n = 4
Output: 3
Explanation: After calling your read method, buf should contain "abc". We read a total of 3 characters from the file, so return 3. Note that "abc" is the file's content, not buf. buf is the destination buffer that you will have to write the results to.

Example 2:

1
2
3
Input: file = "abcde", n = 5
Output: 5
Explanation: After calling your read method, buf should contain "abcde". We read a total of 5 characters from the file, so return 5.

Example 3:

1
2
3
Input: file = "abcdABCD1234", n = 12
Output: 12
Explanation: After calling your read method, buf should contain "abcdABCD1234". We read a total of 12 characters from the file, so return 12.

Example 4:

1
2
3
Input: file = "leetcode", n = 5
Output: 5
Explanation: After calling your read method, buf should contain "leetc". We read a total of 5 characters from the file, so return 5.

Note:

  • Consider that you cannot manipulate the file directly, the file is only accesible for read4 but not for read.

  • The read function will only be called once for each test case.

  • You may assume the destination buffer array, buf, is guaranteed to have enough space for storing n characters.

Explanation

  1. In this problem, we need to store n characters into the buf[], so we cannot directly pass the input buf[] into read4(). Instead, we can call read4() with a temporary buffer array, then copy the temporary buffer array’s content into buf[]. When we copying, we need to record both buf[] and temp[]’s index as bufIdx and tempIdx. At the end, we need to return the file’s content length which is the bufIdx.

  2. First, we call cnt = read4(temp) where temp[] stores the content and cnt it’s the content length. While cnt is not equal to 0 and bufIdx is less than n, we start copying temp[tempIdx] into buf[bufIdx]. If we finish reading temporary buffer’s content, then we call the read4() function and update the content length cnt, and also reset tempIdx back to 0.

  3. Outside the while loop, it’s either the content length is 0 or bufIdx is equal to n, so we stop and return the bufIdx which is the number of character we read.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * The read4 API is defined in the parent class Reader4.
 *     int read4(char[] buf4);
 */

public class Solution extends Reader4 {
    /**
     * @param buf Destination buffer
     * @param n   Number of characters to read
     * @return    The number of actual characters read
     */
    public int read(char[] buf, int n) {
        // if (n == 4) return read4(buf);
        char[] temp = new char[4];
        int bufIdx = 0;
        int tempIdx = 0;

        int cnt = read4(temp);
        while (cnt != 0 && bufIdx < n) {
            buf[bufIdx] = temp[tempIdx];
            bufIdx += 1;
            tempIdx += 1;
            if (tempIdx == cnt) {
                cnt = read4(temp);
                tempIdx = 0;
            }
        }

        return bufIdx;
    }
}

Largest Time for Given Digits

Given an array of 4 digits, return the largest 24 hour time that can be made.

The smallest 24 hour time is 00:00, and the largest is 23:59. Starting from 00:00, a time is larger if more time has elapsed since midnight.

Return the answer as a string of length 5. If no valid time can be made, return an empty string.

Example 1:

1
2
Input: [1,2,3,4]
Output: "23:41"

Example 2:

1
2
Input: [5,5,5,5]
Output: ""

Note:

  1. A.length == 4

  2. 0 <= A[i] <= 9

Explanation

  1. We can find all 4! number of permutations and compare them to get the largest time.

  2. The result will be hh:mm. We can loop the input array trying all possibilities for the first h, second h, first m and second m. Instead of 4 loops, we can have 3 loops because there are total 4 digits, if we know 3 digits, then we will know the last digit.

  3. To validate hh is from 00 to 23, we can actually compare hh and "23" in string format (think about “abc” < “acb”) and make sure "hh" <= "23". Similarlly for mm cannot greater than "59".

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func largestTimeFromDigits(A []int) string {
    res := ""
    for i := 0; i < 4; i++ {
        for j := 0; j < 4; j++ {
            for k := 0; k < 4; k++ {
                if i == j || j == k || k == i { continue }
                hh := strconv.Itoa(A[i]) + strconv.Itoa(A[j])
                mm := strconv.Itoa(A[k]) + strconv.Itoa(A[6-i-j-k])
                temp := hh + ":" + mm
                if hh <= "23" && mm <= "59" && temp > res {
                    res = temp
                }
            }
        }
    }
    return res
}

Contains Duplicate III

Given an array of integers, find out whether there are two distinct indices i and j in the array such that the absolute difference between nums[i] and nums[j] is at most t and the absolute difference between i and j is at most k.

Example 1:

1
2
Input: nums = [1,2,3,1], k = 3, t = 0
Output: true

Example 2:

1
2
Input: nums = [1,0,1,1], k = 1, t = 2
Output: true

Example 3:

1
2
Input: nums = [1,5,9,1,5,9], k = 2, t = 3
Output: false

Hint 1:

Time complexity O(n logk) - This will give an indication that sorting is involved for k elements.

Hint 2:

Use already existing state to evaluate next state - Like, a set of k sorted numbers are only needed to be tracked. When we are processing the next number in array, then we can utilize the existing sorted state and it is not necessary to sort next overlapping set of k numbers again.

Explanation

  1. We can use brute force to solve this problem. We loop all pair of numbers by using 2 loops and compare these two numbers. If their absolute difference is less than or equal to t, then return true.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func containsNearbyAlmostDuplicate(nums []int, k int, t int) bool {
    for i := 0; i < len(nums); i++ {
        for j := i + 1; j < len(nums) && j <= i + k; j++ {
            if abs(nums[i] - nums[j]) <= t {
                return true
            }
        }
    }
    return false
}

func abs(a int) int {
    if a < 0 {
        return -a
    } else {
        return a
    }
}

Repeated Substring Pattern

Given a non-empty string check if it can be constructed by taking a substring of it and appending multiple copies of the substring together. You may assume the given string consists of lowercase English letters only and its length will not exceed 10000.

Example 1:

1
2
3
Input: "abab"
Output: True
Explanation: It's the substring "ab" twice.

Example 2:

1
2
Input: "aba"
Output: False

Example 3:

1
2
3
Input: "abcabcabcabc"
Output: True
Explanation: It's the substring "abc" four times. (And the substring "abcabc" twice.)

Explanation

  1. We can append the input string at the end of the input string. For example, if input string is abab then after appending, the new string is abababab.

  2. Then, we check if the original string is inside the new string’s substrring newStr.substring[1:-1]. If inside, we return true. Otherwise, return false.

Solution

1
2
3
4
func repeatedSubstringPattern(s string) bool {
    ss := s + s
    return strings.Contains(ss[1:len(ss)-1], s)
}

Partition Labels

A string S of lowercase English letters is given. We want to partition this string into as many parts as possible so that each letter appears in at most one part, and return a list of integers representing the size of these parts.

Example 1:

1
2
3
4
5
6
Input: S = "ababcbacadefegdehijhklij"
Output: [9,7,8]
Explanation:
The partition is "ababcbaca", "defegde", "hijhklij".
This is a partition so that each letter appears in at most one part.
A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less parts.

Note:

  • S will have length in range [1, 500].

  • S will consist of lowercase English letters ('a' to 'z') only.

Hint 1:

Try to greedily choose the smallest partition that includes the first letter. If you have something like “abaccbdeffed”, then you might need to add b. You can use an map like “last[‘b’] = 5” to help you expand the width of your partition.

Explanation

  1. In this problem, the same characters can only be inside one group, and we need to make sure the there are as many groups as possible.

  2. We notice that if a character appears many times, then the last same character and the current character are in the same group. From the problem’s example, character a, e, j are the last appear character in each group. So we need to find out every character’s last seen index.

  3. Next, we use a variable end represents the potential group or substring’s ending index, and start represent the group’s first index. They both initialize to 0. Then, we loop through the input string characters, in each iteration, we update the end be the maximum last seen index. If the current index i is equals to end, then we found one group since all the character str[i]’s last seen index is not greater than end, so these characters are in the same group. We can calculate this group’s length be end - start + 1. After we found one group, we need to update start = end + 1.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func partitionLabels(S string) []int {
    lastSeen := make(map[rune]int)
    for i, ch := range S {
        lastSeen[ch] = i
    }

    res := make([]int, 0)
    start, end := 0, 0
    for i, ch := range S {
        end = max(end, lastSeen[ch])
        if i == end {
            res = append(res, i - start + 1)
            start = i + 1
        }
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

All Elements in Two Binary Search Trees

Given two binary search trees root1 and root2.

Return a list containing all the integers from both trees sorted in ascending order.

Example 1:

All Elements in Two Binary Search Trees

1
2
Input: root1 = [2,1,4], root2 = [1,0,3]
Output: [0,1,1,2,3,4]

Example 2:

1
2
Input: root1 = [0,-10,10], root2 = [5,1,7,0,2]
Output: [-10,0,0,1,2,5,7,10]

Example 3:

1
2
Input: root1 = [], root2 = [5,1,7,0,2]
Output: [0,1,2,5,7]

Example 4:

1
2
Input: root1 = [0,-10,10], root2 = []
Output: [-10,0,10]

Example 5:

All Elements in Two Binary Search Trees

1
2
Input: root1 = [1,null,8], root2 = [8,1]
Output: [1,1,8,8]

Constraints:

  • Each tree has at most 5000 nodes.

  • Each node’s value is between [-10^5, 10^5].

Hint 1:

Traverse the first tree in list1 and the second tree in list2.

Hint 2:

Merge the two trees in one list and sort it.

Explanation

  1. We can save space complexity by using the stack way of in-order traversal since the stack way will only save the number of height of the tree nodes, whereas recursive in-order will save all the nodes into a list.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func getAllElements(root1 *TreeNode, root2 *TreeNode) []int {
    res := make([]int, 0)
    cur1, cur2 := root1, root2
    s1, s2 := make([]*TreeNode, 0), make([]*TreeNode, 0)

    for cur1 != nil || cur2 != nil || len(s1) > 0 || len(s2) > 0 {
        for cur1 != nil {
            s1 = append(s1, cur1)
            cur1 = cur1.Left
        }
        for cur2 != nil {
            s2 = append(s2, cur2)
            cur2 = cur2.Left
        }
        if len(s2) == 0 || len(s1) > 0 && s1[len(s1)-1].Val < s2[len(s2)-1].Val {
            cur1 = s1[len(s1)-1]
            s1 = s1[:len(s1)-1]
            res = append(res, cur1.Val)
            cur1 = cur1.Right
        } else {
            cur2 = s2[len(s2)-1]
            s2 = s2[:len(s2)-1]
            res = append(res, cur2.Val)
            cur2 = cur2.Right
        }
    }

    return res
}

Image Overlap

Two images A and B are given, represented as binary, square matrices of the same size. (A binary matrix has only 0s and 1s as values.)

We translate one image however we choose (sliding it left, right, up, or down any number of units), and place it on top of the other image. After, the overlap of this translation is the number of positions that have a 1 in both images.

(Note also that a translation does not include any kind of rotation.)

What is the largest possible overlap?

Example 1:

1
2
3
4
5
6
7
8
Input: A = [[1,1,0],
            [0,1,0],
            [0,1,0]]
       B = [[0,0,0],
            [0,1,1],
            [0,0,1]]
Output: 3
Explanation: We slide A to right by 1 unit and down by 1 unit.

Notes:

  1. 1 <= A.length = A[0].length = B.length = B[0].length <= 30

  2. 0 <= A[i][j], B[i][j] <= 1

Explanation

  1. This problem askes we can move the entire square left, right, up, or down. Then find the maximum number of overlap 1s. We can use brute force to solve this problem.

  2. In one helper function, we fix A and move B down right. Then this is the same as move A up left and fix B. We can use 2 for loops to try all possibility of moving B down and right, then inside these 2 for loops, we create a counter cur to keep track of the number of overlapping 1s. Then we use another 2 for loops to iterate the overlapping part and count the overlap 1s. After counting, we update the global maximum of counter res. Outside these 4 for loops, we return the global maximum counter res.

  3. In another helper function, we fix A and move B up right. This is the same as move A down left and fix B. Similarlly to the above helper function, we will use 4 for loops to calculate the maximum number of overlapping 1s.

  4. At the end, we return the maximum from the these 2 helper functions.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
func largestOverlap(A [][]int, B [][]int) int {
    a := max(helper(A, B), helper(B, A))
    b := max(helper2(A, B), helper(B, A))
    return max(a, b)
}

func helper(A, B [][]int) int {
    res := 0
    n := len(A)

    for moveDown := 0; moveDown < n; moveDown++ {
        for moveRight := 0; moveRight < n; moveRight++ {
            cur := 0
            for r := moveDown; r < n; r++ {
                for c := moveRight; c < n; c++ {
                    if A[r][c] == 1 && B[r-moveDown][c-moveRight] == 1 {
                        cur += 1
                    }
                }
            }
            res = max(res, cur)
        }
    }

    return res
}

func helper2(A, B [][]int) int {
    res := 0
    n := len(A)

    for moveUp := 0; moveUp < n; moveUp++ {
        for moveRight := 0; moveRight < n; moveRight++ {
            cur := 0
            for r := moveUp; r < n; r++ {
                for c := moveRight; c < n; c++ {
                    if A[r-moveUp][c] == 1 && B[r][c-moveRight] == 1 {
                        cur += 1
                    }
                }
            }
            res = max(res, cur)
        }
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Word Pattern

Given a pattern and a string str, find if str follows the same pattern.

Here follow means a full match, such that there is a bijection between a letter in pattern and a non-empty word in str.

Example 1:

1
2
Input: pattern = "abba", str = "dog cat cat dog"
Output: true

Example 2:

1
2
Input:pattern = "abba", str = "dog cat cat fish"
Output: false

Example 3:

1
2
Input: pattern = "aaaa", str = "dog cat cat dog"
Output: false

Example 4:

1
2
Input: pattern = "abba", str = "dog dog dog dog"
Output: false

Notes:

You may assume pattern contains only lowercase letters, and str contains lowercase letters that may be separated by a single space.

Explanation

  1. We can use a hashmap to solve this problem.

  2. First we check if the pattern length is not equal to the word length, then we simply return false. In the hashmap, we store key as pattern character, value as the word. Loop through each word.

  3. If the hashmap doesn’t have the current pattern character as key, then we check if the current word is also not visited before, then we add the character and word into the map, and add the word into the visited set. But if the current word is visited before, then we return false. One example is pattern = "abc", str = "dog dog dog". In this example, the map doesn’t have the pattern before, but the word is visited before, so we return false.

  4. If the hashmap have the current pattern character as key, then we simply compare its corresponding word with the iterated word. If they are not equal, then we return false.

  5. After looping every character and word, we return true.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func wordPattern(pattern string, str string) bool {
    wordArr := strings.Fields(str)
    if len(pattern) != len(wordArr) { return false }

    hm := make(map[byte]string)
    visited := make(map[string]bool)

    for i := 0; i < len(pattern); i++ {
        ch := pattern[i]
        word := wordArr[i]

        if _, ok := hm[ch]; !ok {
            if _, ok := visited[word]; !ok {
                hm[ch] = word
                visited[word] = true
            } else {
                return false
            }
        } else {
            if hm[ch] != word { return false }
        }
    }

    return true
}

Week 2: September 8th - September 14th

Moving Average from Data Stream

Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.

Example:

1
2
3
4
5
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3

Explanation 1

  1. We can use a queue as out sliding window. In the constructor method, we need to instinatiate the limit size, the sum, and the queue.

  2. In the next method, first we check if the queue’s size is equal to the limit size, then we poll the first element out from the queue, and sum needs to subtract this poll element. Next, we add the input val into the queue, and update the sum. Now, we can return the result as sum / queueSize.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class MovingAverage {
    Queue<Integer> queue;
    int sum;
    int size;

    /** Initialize your data structure here. */
    public MovingAverage(int size) {
        this.queue = new LinkedList<>();
        this.sum = 0;
        this.size = size;
    }

    public double next(int val) {
        if (queue.size() == this.size) {
            sum -= queue.poll();
        }
        queue.offer(val);
        sum += val;
        return (double) sum / queue.size();
    }
}

/**
 * Your MovingAverage object will be instantiated and called as such:
 * MovingAverage obj = new MovingAverage(size);
 * double param_1 = obj.next(val);
 */

Explanation 2

  1. We can also use an array instead of queue to solve this problem. First, we need to create an array that has the same size as the limit size. How do we know which element we need to poll? We can use tailIdx = (tailIdx + 1) % limitSize to point to the next index that we will insert the element on. Now tailIdx is in a loop of repeated value, if we have the same size as the limit size, the next index will be the oldest or first index we inserted. Before we update the sum and insert the element in tailIdx of the array, we need to subtract arr[tailIdx] from sum because initially arr[tailIdx] = 0 which is fine to subtract 0. But if arr[tailIdx] is not 0, that means we exceed the limit size so we need to subtract arr[tailIdx] from sum.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class MovingAverage {
    int[] arr;
    int sum;
    int size;
    int cnt;
    int tailIdx;

    /** Initialize your data structure here. */
    public MovingAverage(int size) {
        this.arr = new int[size];
        this.size = size;
    }

    public double next(int val) {
        if (cnt < this.size) {
            cnt += 1;
        }
        sum -= arr[tailIdx];
        arr[tailIdx] = val;
        sum += val;
        tailIdx = (tailIdx + 1) % this.size;
        return 1.0 * sum / cnt;
    }
}

/**
 * Your MovingAverage object will be instantiated and called as such:
 * MovingAverage obj = new MovingAverage(size);
 * double param_1 = obj.next(val);
 */

Sum of Root To Leaf Binary Numbers

Given a binary tree, each node has value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit. For example, if the path is 0 -> 1 -> 1 -> 0 -> 1, then this could represent 01101 in binary, which is 13.

For all leaves in the tree, consider the numbers represented by the path from the root to that leaf.

Return the sum of these numbers.

Example 1:

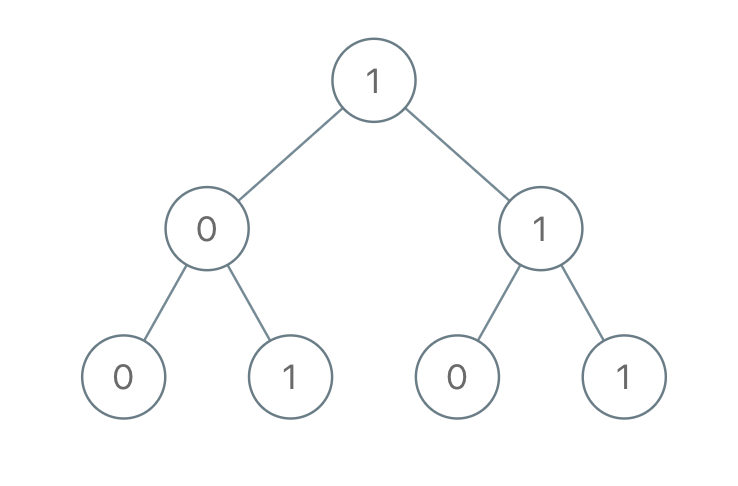
Sum of Root To Leaf Binary Numbers

1
2
3
Input: [1,0,1,0,1,0,1]
Output: 22
Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22

Note:

  1. The number of nodes in the tree is between 1 and 1000.

  2. node.val is 0 or 1.

  3. The answer will not exceed 2^31 - 1.

Hint 1:

Find each path, then transform that path to an integer in base 10.

Explanation

  1. We can use recursion to solve this problem. For example, in the problem’s example, we need to pass the current root value 1 to both its left child and right child. When we are in the left child, we need to left shift the passed value 1 by 1 then add the current node’s value, in other words, we get (1 << 1) + 0 = 10 in binary format. Similarlly, in the right child, we get (1 << 1) + 1 = 11 in binary format.

  2. In the main function, we start the helper function with root and 0. The base case is if the root is null, we return 0. After we update the current value, if root is leaf, we return the updated current value. Else, we return the sum of helper(root.left, updatedCurVal) and helper(root.right, updatedCurVal).

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func sumRootToLeaf(root *TreeNode) int {
    return helper(root, 0)
}

func helper(root *TreeNode, cur int) int {
    if root == nil { return 0 }

    cur <<= 1
    cur += root.Val

    if root.Left == nil && root.Right == nil {
        return cur
    }

    return helper(root.Left, cur) + helper(root.Right, cur)
}

Compare Version Numbers

Compare two version numbers version1 and version2.

If version1 > version2 return 1; if version1 < version2 return -1; otherwise return 0.

You may assume that the version strings are non-empty and contain only digits and the . character.

The . character does not represent a decimal point and is used to separate number sequences.

For instance, 2.5 is not “two and a half” or “half way to version three”, it is the fifth second-level revision of the second first-level revision.

You may assume the default revision number for each level of a version number to be 0. For example, version number 3.4 has a revision number of 3 and 4 for its first and second level revision number. Its third and fourth level revision number are both 0.

Example 1:

1
2
Input: version1 = "0.1", version2 = "1.1"
Output: -1

Example 2:

1
2
Input: version1 = "1.0.1", version2 = "1"
Output: 1

Example 3:

1
2
Input: version1 = "7.5.2.4", version2 = "7.5.3"
Output: -1

Example 4:

1
2
3
Input: version1 = "1.01", version2 = "1.001"
Output: 0
Explanation: Ignoring leading zeroes, both “01” and “001" represent the same number “1”

Example 5:

1
2
3
Input: version1 = "1.0", version2 = "1.0.0"
Output: 0
Explanation: The first version number does not have a third level revision number, which means its third level revision number is default to "0"

Note:

  1. Version strings are composed of numeric strings separated by dots . and this numeric strings may have leading zeroes.

  2. Version strings do not start or end with dots, and they will not be two consecutive dots.

Explanation

  1. We can split the version string by . and convert the substring to integer and compare their version.

  2. If one string finish splitting, in other word, another string has more length, then we can make the short string as 0 by default and compare the long substring.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func compareVersion(version1 string, version2 string) int {
    v1 := strings.Split(version1, ".")
    v2 := strings.Split(version2, ".")
    idx1, idx2 := 0, 0

    for idx1 < len(v1) || idx2 < len(v2) {
        n1, n2 := 0, 0
        if idx1 < len(v1) {
            n1, _ = strconv.Atoi(v1[idx1])
        }
        if idx2 < len(v2) {
            n2, _ = strconv.Atoi(v2[idx2])
        }

        if n1 < n2 {
            return -1
        }
        if n1 > n2 {
            return 1
        }

        idx1 += 1
        idx2 += 1
    }

    return 0
}

Bulls and Cows

You are playing the following Bulls and Cows game with your friend: You write down a number and ask your friend to guess what the number is. Each time your friend makes a guess, you provide a hint that indicates how many digits in said guess match your secret number exactly in both digit and position (called “bulls”) and how many digits match the secret number but locate in the wrong position (called “cows”). Your friend will use successive guesses and hints to eventually derive the secret number.

Write a function to return a hint according to the secret number and friend’s guess, use A to indicate the bulls and B to indicate the cows.

Please note that both secret number and friend’s guess may contain duplicate digits.

Example 1:

1
2
3
4
5
Input: secret = "1807", guess = "7810"

Output: "1A3B"

Explanation: 1 bull and 3 cows. The bull is 8, the cows are 0, 1 and 7.

Example 2:

1
2
3
4
5
Input: secret = "1123", guess = "0111"

Output: "1A1B"

Explanation: The 1st 1 in friend's guess is a bull, the 2nd or 3rd 1 is a cow.

Note: You may assume that the secret number and your friend’s guess only contain digits, and their lengths are always equal.

Explanation

  1. We can also solve this problem using one iteration. We will create an array arr of size 10 to count the increment of secretChar and decrement of guessChar.

  2. Loop through either one of the string, if both secret and guess’s current character is the same, then we increase bull. Else, we check if arr[secretChar] is less than 0, if true, then we increase cow, and no matter it is less than 0 or geater than or equal to zero, we will increase arr[secretChar]. Then, we check if arr[guessChar] is greater than 0, if true, then we increase cow, and no matter it is greater than 0 or less than or equal to zero, we will decrease arr[guessChar].

  3. We do this because in the next iteration, if arr[secretChar] is less than 0, that means in the previous iterations, guessChar appeared had appeared. Similarlly, if arr[guessChar] is greater than 0, that means secretChar had appeared in the previous iterations.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func getHint(secret string, guess string) string {
    bull, cow := 0, 0
    arr := make([]int, 10)

    for i := 0; i < len(secret); i++ {
        secretChar := secret[i]
        guessChar := guess[i]
        if (secretChar == guessChar) {
            bull += 1
        } else {
            if arr[secretChar - '0'] < 0 { cow += 1 }
            if arr[guessChar - '0'] > 0 { cow += 1 }
            arr[secretChar - '0'] += 1
            arr[guessChar - '0'] -= 1
        }
    }

    return strconv.Itoa(bull) + "A" + strconv.Itoa(cow) + "B"
}

Maximum Product Subarray

Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.

Example 1:

1
2
3
Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

Example 2:

1
2
3
Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

Explanation

  1. We can solve this problem in one loop. In each iteration, we need to keep track of the maximum result ending here curMax, and minimum result ending here curMin. We can initialize curMax, curMin, and result res all be the first number of the array.

  2. Start from the second number, let say when we are on the ith number, if the ith number is positive, then we use the current maximum number multiple by it in order to get the maximum result. If the ith number is negative, then we use the current minimum number multiple by it to get the maximum result. Therefore, no matter the ith number is positive or negative, we can get the maximum result by curMax = max(nums[i], curMax * nums[i], curMin * nums[i]). Similarlly, we can get the minimum result by curMin = min(nums[i], curMax * nums[i], curMin * nums[i]). After getting curMax and curMin, we will update the result res = max(res, curMax).

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func maxProduct(nums []int) int {
    res := nums[0]
    curMax, curMin := nums[0], nums[0]

    for i := 1; i < len(nums); i++ {
        temp := curMax
        curMax = max(nums[i], max(curMax * nums[i], curMin * nums[i]))
        curMin = min(nums[i], min(temp * nums[i], curMin * nums[i]))
        res = max(res, curMax)
    }

    return res
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

Combination Sum III

Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.

Note:

  • All numbers will be positive integers.

  • The solution set must not contain duplicate combinations.

Example 1:

1
2
Input: k = 3, n = 7
Output: [[1,2,4]]

Example 2:

1
2
Input: k = 3, n = 9
Output: [[1,2,6], [1,3,5], [2,3,4]]

Explanation

  1. We can use backtracking to solve this problem. First we initialize a result list, a temperoary sublist. In the DFS helper function, we will pass these two lists and the k and n, also the starting number, which is 1.

  2. Inside the helper function, the base case is if the temperoary sublist’s size is equal to k, then we also check if n is zero, then we add the sublist to the result list, and we will return immediatly. Another basecase is if start is greater than n, then we return immediately. If no base case satisfy, then we will loop start from start to 9, recursivly calling the helper function, adding the iterative number to the sublist and update the start = i + 1 and n = n - i. After the helper function, remember remove the added number. Then it will add the next iterative number.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
func combinationSum3(k int, n int) [][]int {
    res := make([][]int, 0)
    cur := make([]int, 0)
    helper(k, n, cur, &res, 1)
    return res
}

func helper(k int, n int, cur []int, res*[][]int, start int) {
    if len(cur) == k {
        if n == 0 {
            temp := make([]int, k)
            copy(temp, cur)
            *res = append(*res, temp)
        }
        return
    }

    if start > n { return }

    for i := start; i <= 9; i++ {
        cur = append(cur, i)
        helper(k, n-i, cur, res, i+1)
        cur = cur[:len(cur)-1]
    }
}

Insert Interval

Given a set of non-overlapping intervals, insert a new interval into the intervals (merge if necessary).

You may assume that the intervals were initially sorted according to their start times.

Example 1:

1
2
Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]

Example 2:

1
2
3
Input: intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
Output: [[1,2],[3,10],[12,16]]
Explanation: Because the new interval [4,8] overlaps with [3,5],[6,7],[8,10].

NOTE: input types have been changed on April 15, 2019. Please reset to default code definition to get new method signature.

Explanation

  1. We need to draw a picture to illustrate this problem.

    1
    2
    3
    4
       original interval: - - - - - -      - - - - -           - - - - -             - - - - - -
   added interval:                           - - - - - - - - - - - - - - -

   result:            - - - - - -      - - - - - - - - - - — - - - - - - -       - - - - - - -

  2. Iterate the original interval, if the interval’s end is greater than the added interval’s start, then they can merge, and we choose the smallest starting point between these two as the merge interval’s starting point. Then keep iterating, until the current interval’s start is greater than the added interval’s end, then we compare the previous interval with the added interval’s ending point and choose the greater ending point as the merge interval’s ending point.

    1
    2
    3
    4
     original interval: - - - - - -   - - - - -                   - - - - -            - - - - -
 added interval:                                 - - - -

 result:            - - - - - -    - - - - -     - - - -      — - - - -             - - - - -

  3. In the above case, step2’s method also apply.

    1
    2
    3
    4
     original interval:               - - - - -            - - - - -
 added interval:     - - - -

 result:             - - - -      - - - - -             — - - - -

  4. In the above case, we can initialize the merge inteval’s starting point and ending point as the added interval’s start and ending point.

    1
    2
    3
    4
     original interval:  - - - - -            - - - -
 added interval:                                        - - - - -

 result:             - - - - -            - - - -       - - - - -

  5. In the above case, after iterate to the last interval and we haven’t find the merge interval, we can just added the added interval to the result and return the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
func insert(intervals [][]int, newInterval []int) [][]int {
    res := make([][]int, 0)
    idx := 0
    nStart, nEnd := newInterval[0], newInterval[1]

    for idx < len(intervals) && intervals[idx][1] < newInterval[0] {
        res = append(res, intervals[idx])
        idx += 1
    }

    for idx < len(intervals) && intervals[idx][0] <= newInterval[1] {
        nStart = min(nStart, intervals[idx][0])
        nEnd = max(intervals[idx][1], newInterval[1])
        idx += 1
    }
    res = append(res, []int{nStart, nEnd})

    for idx < len(intervals) {
        res = append(res, intervals[idx])
        idx += 1
    }

    return res
}

func min(a, b int) int {
    if a < b {
        return a
    } else {
        return b
    }
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

Example 1:

1
2
3
4
Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
             Total amount you can rob = 1 + 3 = 4.

Example 2:

1
2
3
4
Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
             Total amount you can rob = 2 + 9 + 1 = 12.

Constraints:

  • 0 <= nums.length <= 100

  • 0 <= nums[i] <= 400

Explanation

  1. We can use dynamic programming to solve this problem.

  2. Dynamic state is creating a one dimensional array dp. dp[i] means the total maximum money when rob start from the first house to the index i house.

  3. Dynamic init. For example if nums = [3, 2, 1, 5], then in index0 dp[0] = 3; then in index1, dp[1] = 3 because 3 > 2.

  4. Dyamic function. In index2, because we cannot rob the adjancent houses, so if we rob the current index2 house, then we cannot rob index1 house, in other word, if we rob index2, then dp[2] = dp[0] + nums[2]; if we don’t rob index2 house, then dp[2] = dp[1]; so we can take the maximum of rob or not rob, which is max(dp[0]+nums[2], dp[1]). Therefore, dynamic function is dp[i] = max(dp[i-2] + nums[i], dp[i-1]).

  5. Dynamic result is returning the last index of dp.

  6. Since dp[i] is only depends on dp[i-2] and dp[i-1], we can store these two as variables and save space.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func rob(nums []int) int {
    if len(nums) == 0 { return 0 }
    if len(nums) == 1 { return nums[0] }

    prevMax := nums[0]
    curMax := max(nums[0], nums[1])

    for i := 2; i < len(nums); i++ {
        temp := curMax
        curMax = max(curMax, prevMax + nums[i])
        prevMax = temp
    }

    return curMax
}

func max(a, b int) int {
    if a < b {
        return b
    } else {
        return a
    }
}

Week 3: September 15th - September 21st

Inorder Successor in BST II

Given a node in a binary search tree, find the in-order successor of that node in the BST.

If that node has no in-order successor, return null.

The successor of a node is the node with the smallest key greater than node.val.

You will have direct access to the node but not to the root of the tree. Each node will have a reference to its parent node. Below is the definition for Node:

1
2
3
4
5
6
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

Follow up:

Could you solve it without looking up any of the node’s values?

Example 1:

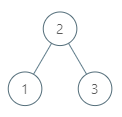
Inorder Successor in BST II

1
2
3
Input: tree = [2,1,3], node = 1
Output: 2
Explanation: 1's in-order successor node is 2. Note that both the node and the return value is of Node type.

Example 2:

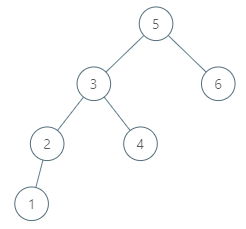
Inorder Successor in BST II

1
2
3
Input: tree = [5,3,6,2,4,null,null,1], node = 6
Output: null
Explanation: There is no in-order successor of the current node, so the answer is null.

Example 3:

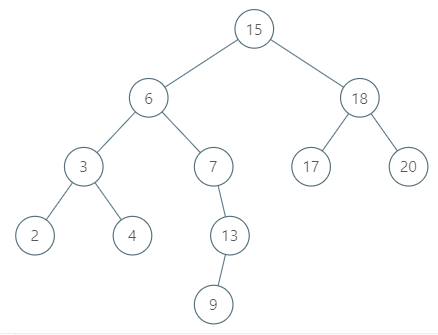
Inorder Successor in BST II

1
2
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 15
Output: 17

Example 4:

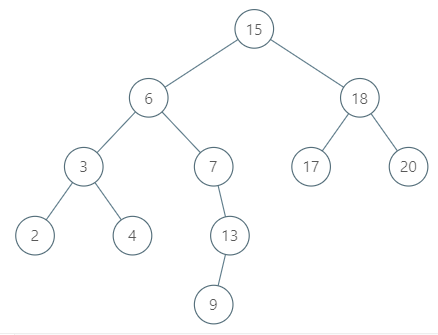
Inorder Successor in BST II

1
2
Input: tree = [15,6,18,3,7,17,20,2,4,null,13,null,null,null,null,null,null,null,null,9], node = 13
Output: 15

Example 5:

1
2
Input: tree = [0], node = 0
Output: null

Constraints:

  • -10^5 <= Node.val <= 10^5

  • 1 <= Number of Nodes <= 10^4

  • All Nodes will have unique values.

Explanation

  1. To find the inorder successor, we have two cases.

  2. The first case is if the node has right child, then the inorder successor is the node’s right child’s most left child node.

  3. The second case is if the node doesn’t have right child, then the inorder success is the node’s parent node, and we will traverse up until the parent node has value greater than node’s value. Then the result is this parent node.

Solution 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node inorderSuccessor(Node node) {
        Node res;
        if (node.right != null) {
            res = node.right;
            while (res.left != null) {
                res = res.left;
            }
        } else {
            res = node.parent;
            while (res != null && res.val < node.val) {
                res = res.parent;
            }
        }
        return res;
    }
}

Explanation 2

  1. For the second case, we can achieve it by not comparing value. We will traverse up until the current node is the left child of the current node’s parent node. Then the result is the current node’s parent node.

Solution 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node inorderSuccessor(Node node) {
        Node res;
        if (node.right != null) {
            res = node.right;
            while (res.left != null) {
                res = res.left;
            }
        } else {
            res = node;
            while (res != null && res.parent != null && res != res.parent.left) {
                res = res.parent;
            }
            res = res.parent;
        }
        return res;
    }
}

Length of Last Word

Given a string s consists of upper/lower-case alphabets and empty space characters ' ', return the length of last word (last word means the last appearing word if we loop from left to right) in the string.

If the last word does not exist, return 0.

Note: A word is defined as a maximal substring consisting of non-space characters only.

Example:

1
2
Input: "Hello World"
Output: 5

Explanation

  1. We can solve it in one line. First trim the string and get its length len, then subtract 1 is the last index, then again subtract the last index of space of the trimmed string, which returns us the last word’s length.

  2. The second way is create a pointer that starts from the end, find the last character’s index, then set the result counter to 0. Increase 1 until the pointer poinits to empty space. Return the counter result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
func lengthOfLastWord(s string) int {
    for i := len(s)-1; i >= 0; i-- {
        if s[i] != ' ' {
            res := 0
            for i >= 0 && s[i] != ' ' {
                res += 1
                i -= 1
            }
            return res
        }
    }
    return 0
}

Maximum XOR of Two Numbers in an Array

Given an integer array nums, return the maximum result of nums[i] XOR nums[j], where 0 ≤ i ≤ j < n.

Follow up: Could you do this in O(n) runtime?

Example 1:

1
2
3
Input: nums = [3,10,5,25,2,8]
Output: 28
Explanation: The maximum result is 5 XOR 25 = 28.

Example 2:

1
2
Input: nums = [0]
Output: 0

Example 3:

1
2
Input: nums = [2,4]
Output: 6

Example 4:

1
2
Input: nums = [8,10,2]
Output: 10

Example 5:

1
2
Input: nums = [14,70,53,83,49,91,36,80,92,51,66,70]
Output: 127

Constraints:

  • 1 <= nums.length <= 2 * 10^4

  • 0 <= nums[i] <= 2^31 - 1

Explanation

  1. We know that if a ^ b = x, then a ^ x = b.

  2. For example to find the result’s highest bit. We put all numbers highest bit into a HashSet, then use 1 to XOR all numbers in the HashSet. If the result is inside the HashSet, that means the result’s highest bit is 1, not 0. In other words, we first assume the result’s highest bit is 1, then use 1 to XOR all numbers in the HashSet. If 1 ^ a = b, and b is in the HashSet, that means two numbers from the HashSet XOR can have result 1 (a ^ b = 1), else no two numbers from the HashSet is equals to 1, so the assumption is wrong, and the highest bit is 0. Similarlly, we can find the result’s second bit, third bit, etc.

  3. To find the result’s n bits, we put all numbers’ first left n bit into the HashSet. Then we use the result’s first left n-1 bit OR the nth bit which is 1 because we assume the nth bit is 1. Then use this temp result to XOR all numbers in the HashSet. If the XOR result is inside the HashSet, then temp is the result’s first n bit result.

  4. For example, if input array is [14, 11, 7, 2], its binary form is [1110, 1011, 0111, 0010], we can start from the fourth bit since know input has 4 bits. So i=3.

    1
    2
    3
    4
         1. i = 3, set = {1000, 0000} => max = 1000
     2. i = 2, set = {1100, 1000, 0100, 0000} => max = 1100 because temp = 1000 | 0100, then temp XOR all numbers from the set.
     3. i = 1, set = {1110, 1010, 0110, 0010} => max = 1100
     4. i = 0, set = {1110, 1011, 0111, 0010} => max = 1100

    Final answer is 1100 => 12, 1011 ^ 0111 = 1100(11 ^ 7 = 12).

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func findMaximumXOR(nums []int) int {
    res := 0
    mask := 0

    for i := 31; i >= 0; i-- {
        mask = mask | (1 << i)
        set := make(map[int]bool)
        for _, num := range nums {
            set[num & mask] = true
        }

        temp := res | (1 << i)
        for pre := range set {
            if set[pre ^ temp] == true {
                res = temp
                break
            }
        }
    }

    return res
}

Robot Bounded In Circle

On an infinite plane, a robot initially stands at (0, 0) and faces north. The robot can receive one of three instructions:

  • "G": go straight 1 unit;

  • "L": turn 90 degrees to the left;

  • "R": turn 90 degress to the right.

The robot performs the instructions given in order, and repeats them forever.

Return true if and only if there exists a circle in the plane such that the robot never leaves the circle.

Example 1:

1
2
3
4
5
Input: "GGLLGG"
Output: true
Explanation:
The robot moves from (0,0) to (0,2), turns 180 degrees, and then returns to (0,0).
When repeating these instructions, the robot remains in the circle of radius 2 centered at the origin.

Example 2:

1
2
3
4
Input: "GG"
Output: false
Explanation:
The robot moves north indefinitely.

Example 3:

1
2
3
4
Input: "GL"
Output: true
Explanation:
The robot moves from (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ...

Note:

  1. 1 <= instructions.length <= 100

  2. instructions[i] is in {'G', 'L', 'R'}

Hint 1:

Calculate the final vector of how the robot travels after executing all instructions once - it consists of a change in position plus a change in direction.

Hint 2:

The robot stays in the circle iff (looking at the final vector) it changes direction (ie. doesn’t stay pointing north), or it moves 0.

Explanation

  1. From the hint, we know that after executing all the instructions, if the current position is (0, 0) or the current direction is changed, then we have circle.

  2. First, we initialize the top, right, bottom, left direction diff dirs as [(0, 1), (1, 0), (0, -1), (-1, 0)], the direction index d is 0, and we initialize the current x, y position as (0, 0).

  3. If the current instruction is 'G', then we update curX += dirs[d][0] and curY += dirs[d][1]. Else if the current instruction is 'L', then we only need to update the direction index as (d + 3) % 4 because the left direction diff is at index 3 base on the initialization we defined. Else if the current instruction is 'R', then we update the direction index as (d + 1) % 4.

  4. After looping all instructions, if current position is (0, 0) or current direction index is different than the direction we started, that means there is circle, so we return True, else return False.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func isRobotBounded(instructions string) bool {
    curX, curY := 0, 0
    dirs := [][]int{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}
    d := 0

    for _, instruction := range instructions {
        if instruction == 'L' {
            d = (d + 3) % 4
        } else if instruction == 'R' {
            d = (d + 1) % 4
        } else if instruction == 'G' {
            curX += dirs[d][0]
            curY += dirs[d][1]
        }
    }

    return (curX == 0 && curY == 0) || (d != 0)
}

Best Time to Buy and Sell Stock

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

1
2
3
4
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Example 2:

1
2
3
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Explanation

  1. While we iterating the array, we need to keep track of the minimum element, and in each iteration, we subtract the minimum to get the current profit.

  2. Also, each iteration we need to compare the maximum profit with the current profit.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func maxProfit(prices []int) int {
    maxProfit := 0
    minPrice := math.MaxInt32
    for _, price := range prices {
        minPrice = min(minPrice, price)
        maxProfit = max(maxProfit, price - minPrice)
    }
    return maxProfit
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

func max(a, b int) int {
    if a < b {
        return b
    }
    return a
}

Sequential Digits

An integer has sequential digits if and only if each digit in the number is one more than the previous digit.

Return a sorted list of all the integers in the range [low, high] inclusive that have sequential digits.

Example 1:

1
2
Input: low = 100, high = 300
Output: [123,234]

Example 2:

1
2
Input: low = 1000, high = 13000
Output: [1234,2345,3456,4567,5678,6789,12345]

Constraints:

  • 10 <= low <= high <= 10^9

Hint 1:

Generate all numbers with sequential digits and check if they are in the given range.

Hint 2:

Fix the starting digit then do a recursion that tries to append all valid digits.

Explanation

  1. First creating a string “123456789”, then use a sliding window logic to get the sequential number, then compare the sequential number with low and high and add it to the result list.

  2. If number low has 4 digits, and number high has 5 digits, then we loop from window size 4 to window size 5 inclusive. Inside this for loop, we create an inner for loop to try all possible sequential number that has number of windowSize digits. For example, if the current window size is 4, then the inner for loop will try 1234, 2345, 3456, 4567, 5678, 6789. If the current number is inside the low and high range, then we add it to the result list.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func sequentialDigits(low int, high int) []int {
    res := make([]int, 0)
    digits := "123456789"
    lowLen, highLen := len(strconv.Itoa(low)), len(strconv.Itoa(high))

    for i := lowLen; i <= highLen; i++ {
        for left := 0; left <= len(digits)-i; left++ {
            num, _ := strconv.Atoi(digits[left: left+i])
            if low <= num && num <= high {
                res = append(res, num)
            }
        }
    }

    return res
}

Unique Paths III

On a 2-dimensional grid, there are 4 types of squares:

  • 1 represents the starting square. There is exactly one starting square.

  • 2 represents the ending square. There is exactly one ending square.

  • 0 represents empty squares we can walk over.

  • -1 represents obstacles that we cannot walk over.

Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.

Example 1:

1
2
3
4
5
Input: [[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
Output: 2
Explanation: We have the following two paths:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

Example 2:

1
2
3
4
5
6
7
Input: [[1,0,0,0],[0,0,0,0],[0,0,0,2]]
Output: 4
Explanation: We have the following four paths:
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

Example 3:

1
2
3
4
5
Input: [[0,1],[2,0]]
Output: 0
Explanation:
There is no path that walks over every empty square exactly once.
Note that the starting and ending square can be anywhere in the grid.

Note:

  1. 1 <= grid.length * grid[0].length <= 20

Explanation

  1. We can use DFS brute force to solve this problem. We find out every possible paths from starting square to ending square, once we reach the ending square, we compare the number of zero squares we visited with the total number of zero squares, if they match, then it means we walk over every zero square once.

  2. First, we loop through every square to count the total number of zeros squares and record the starting square’s position.

  3. We start the DFS helper function with the starting position (startRow, startCol) and the total number of zeros zeros. Inside the DFS helper function, the base case are if current position is out of bound, we return 0; if current position is -1, we return 0; if the current position is the ending square, we check if zeros is 0, which mean we visit every zero squares, so we find one path and return 1 else return 0. If the current square is a zero square, then we subtract 1 from zeros. Next, we update the current position to number -1 to mark this position is visited, then recursively call the helper function with the current position’s 4 directions. The totalPaths will be the 4 recursive function’s sum. Next, we need to backtrack this position and change -1 to its original number.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func uniquePathsIII(grid [][]int) int {
    zeros := 0
    startRow, startCol := 0, 0
    for r := 0; r < len(grid); r++ {
        for c := 0; c < len(grid[0]); c++ {
            if grid[r][c] == 0 {
                zeros += 1
            } else if grid[r][c] == 1 {
                startRow = r
                startCol = c
            }
        }
    }

    return helper(grid, startRow, startCol, zeros)
}

func helper(grid [][]int, curRow, curCol, zeros int) int {
    if curRow < 0 || curRow >= len(grid) || curCol < 0 || curCol >= len(grid[0]) {
        return 0
    }
    if grid[curRow][curCol] == -1 {
        return 0
    }
    if grid[curRow][curCol] == 2 {
        if zeros == 0 {
            return 1
        } else {
            return 0
        }
    }
    if grid[curRow][curCol] == 0 {
        zeros -= 1
    }
    temp := grid[curRow][curCol]
    grid[curRow][curCol] = -1
    totalPaths := helper(grid, curRow-1, curCol, zeros) +
                    helper(grid, curRow+1, curCol, zeros) +
                    helper(grid, curRow, curCol-1, zeros) +
                    helper(grid, curRow, curCol+1, zeros)
    grid[curRow][curCol] = temp

    return totalPaths
}

Car Pooling

You are driving a vehicle that has capacity empty seats initially available for passengers. The vehicle only drives east (ie. it cannot turn around and drive west.)

Given a list of trips, trip[i] = [num_passengers, start_location, end_location] contains information about the i-th trip: the number of passengers that must be picked up, and the locations to pick them up and drop them off. The locations are given as the number of kilometers due east from your vehicle’s initial location.

Return true if and only if it is possible to pick up and drop off all passengers for all the given trips.

Example 1:

1
2
Input: trips = [[2,1,5],[3,3,7]], capacity = 4
Output: false

Example 2:

1
2
Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: true

Example 3:

1
2
Input: trips = [[2,1,5],[3,5,7]], capacity = 3
Output: true

Example 4:

1
2
Input: trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11
Output: true

Constraints:

  1. trips.length <= 1000

  2. trips[i].length == 3

  3. 1 <= trips[i][0] <= 100

  4. 0 <= trips[i][1] < trips[i][2] <= 1000

  5. 1 <= capacity <= 100000

Hint 1:

Sort the pickup and dropoff events by location, then process them in order.

Explanation

  1. We can use brute force to solve this problem. Since the constraints trips[i][2] <= 1000, we can create an integer array distance[] that has size 1001. Loop through the trips[], in start location, we add the number of people in distance[startLocation]; in end location, we subtract the number of people in distance[endLocation]. Then loop through the distance[], accumulate the count of number of people cnt += distance[i], if cnt > capacity, then we return false immediately. After the loop, return true.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func carPooling(trips [][]int, capacity int) bool {
    distance := make([]int, 1001)
    for _, trip := range trips {
        distance[trip[1]] += trip[0]
        distance[trip[2]] -= trip[0]
    }

    cnt := 0
    for _, numPeople := range distance {
        cnt += numPeople
        if cnt > capacity {
            return false
        }
    }

    return true
}

Week 4: September 22nd - September 28th

Insert into a Sorted Circular Linked List

Given a node from a Circular Linked List which is sorted in ascending order, write a function to insert a value insertVal into the list such that it remains a sorted circular list. The given node can be a reference to any single node in the list, and may not be necessarily the smallest value in the circular list.

If there are multiple suitable places for insertion, you may choose any place to insert the new value. After the insertion, the circular list should remain sorted.

If the list is empty (i.e., given node is null), you should create a new single circular list and return the reference to that single node. Otherwise, you should return the original given node.

Example 1:

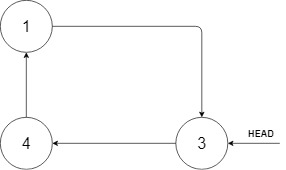
Insert into a Sorted Circular Linked List

1
2
3
Input: head = [3,4,1], insertVal = 2
Output: [3,4,1,2]
Explanation: In the figure above, there is a sorted circular list of three elements. You are given a reference to the node with value 3, and we need to insert 2 into the list. The new node should be inserted between node 1 and node 3. After the insertion, the list should look like this, and we should still return node 3.

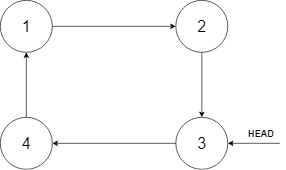
Insert into a Sorted Circular Linked List

Example 2:

1
2
3
Input: head = [], insertVal = 1
Output: [1]
Explanation: The list is empty (given head is null). We create a new single circular list and return the reference to that single node.

Example 3:

1
2
Input: head = [1], insertVal = 0
Output: [1,0]

Constraints:

  • 0 <= Number of Nodes <= 5 * 10^4

  • -10^6 <= Node.val <= 10^6

  • -10^6 <= insertVal <= 10^6

Explanation

  1. First, if the list is empty, then we can create a node with the value equals to the insertVal and make its next pointer pointing to itself.

  2. If the list is not empty, then we need to consider two cases.

    • First case is if the insertVal is in between the minimum node value and maximum node value. This can only happen if the insertVal is greater than the maximum node value or insertVal is less than the minimum node value. For example, from the problem’s example 1, the maximum node value is 4, the minimum node value is 1. If the insertVal is 5 or 0, then insertVal will be inserted between node 4 and node 1.

    • Second case is the general case. For example, from the problem’s example 1, the insertVal is 2. We want to insert 2 in between node 1 and node 3. We can achieve this by creating two pointers pre and cur. We then check if pre.val <= insertVal <= cur.val and insert it after node pre.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
// Definition for a Node.
class Node {
    public int val;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _next) {
        val = _val;
        next = _next;
    }
};
*/

class Solution {
    public Node insert(Node head, int insertVal) {
        if (head == null) {
            Node res = new Node(insertVal);
            res.next = res;
            return res;
        }

        Node pre = head;
        Node cur = pre.next;
        while (cur != head) {
            if (pre.val > cur.val && (insertVal >= pre.val || insertVal <= cur.val)) break;
            if (pre.val <= insertVal && insertVal <= cur.val) break;
            pre = cur;
            cur = cur.next;
        }

        Node insertNode = new Node(insertVal, cur);
        pre.next = insertNode;
        return head;
    }
}

Majority Element II

Given an integer array of size n, find all elements that appear more than ⌊ n/3 ⌋ times.

Note: The algorithm should run in linear time and in O(1) space.

Example 1:

1
2
Input: [3,2,3]
Output: [3]

Example 2:

1
2
Input: [1,1,1,3,3,2,2,2]
Output: [1,2]

Hint 1:

How many majority elements could it possibly have? Do you have a better hint? Suggest it!

Explanation

  1. Similar to 169. Majority Element, this time we need to find elements more than n/3 times. There are must be at most two elements. If there are three elements that have more than $n/3$, then $3 * n/3 > 1$. So, we can use Moore Voting algorithm to find two most appeared numbers.

  2. After we find the two most appeared numbers a and b, we also need to loop one more time of the array to check if countA and countB are actually more than n/3. Because it maybe only one element in the array have more than $n/3$ times.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func majorityElement(nums []int) []int {
    a, b := 0, 0
    cntA, cntB := 0, 0

    for _, num := range nums {
        if num == a {
            cntA += 1
        } else if num == b {
            cntB += 1
        } else if cntA == 0 {
            a = num
            cntA += 1
        } else if cntB == 0 {
            b = num
            cntB += 1
        } else {
            cntA -= 1
            cntB -= 1
        }
    }

    cntA, cntB = 0, 0
    for _, num := range nums {
        if num == a {
            cntA += 1
        } else if num == b {
            cntB += 1
        }
    }

    res := make([]int, 0)
    if cntA > len(nums) / 3 { res = append(res, a) }
    if cntB > len(nums) / 3 { res = append(res, b) }
    return res
}

Gas Station

There are N gas stations along a circular route, where the amount of gas at station i is gas[i].

You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations.

Return the starting gas station’s index if you can travel around the circuit once in the clockwise direction, otherwise return -1.

Note:

  • If there exists a solution, it is guaranteed to be unique.

  • Both input arrays are non-empty and have the same length.

  • Each element in the input arrays is a non-negative integer.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input:
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

Output: 3

Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
Input:
gas  = [2,3,4]
cost = [3,4,3]

Output: -1

Explanation:
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.

Explanation

  1. In order to loop all elements, total gas must equal or greater than total cost, then the start can exist.

  2. If we start from index 0, if current gas is equal or greater than current cost, then we can move forward. After we successfully move forward, we use the remaining gas plus the current gas minus the current cost to get the difference. If the difference is less than 0, that means we cannot start from any indexes between index 0 and current index inclusive. For example, we start from index 0, now when we are on index i, and curGas + gas[i] - cost[i] < 0, we know that after index i-1, curGas >= 0, after index i-2, old_curGas >= 0, etc. Any index before i will only bring positive curGas, so if at index i and the difference is negative, then the start cannot be any index between 0 and i inclusive, so we update start = i + 1. When finish looping, we return start if the total gas is equal or greater than total cost.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func canCompleteCircuit(gas []int, cost []int) int {
    res := 0
    totalGas, totalCost := 0, 0
    curRemainGas := 0
    n := len(gas)

    for i := 0; i < n; i++ {
        totalGas += gas[i]
        totalCost += cost[i]
        curRemainGas += gas[i] - cost[i]
        if curRemainGas < 0 {
            res = i + 1
            curRemainGas = 0
        }
    }

    if totalGas >= totalCost {
        return res
    } else {
        return -1
    }
}

Find the Difference

Given two strings s and t which consist of only lowercase letters.

String t is generated by random shuffling string s and then add one more letter at a random position.

Find the letter that was added in t.

Example:

1
2
3
4
5
6
7
8
9
Input:
s = "abcd"
t = "abcde"

Output:
e

Explanation:
'e' is the letter that was added.

Explanation

  1. We can also use XOR to solve this problem because if two same chacter XOR, it will become zero. If there’s only one character added, then the result will be that character.

Solution

1
2
3
4
5
6
func findTheDifference(s string, t string) byte {
    res := byte(0)
    for i := range s { res ^= s[i] }
    for i := range t { res ^= t[i] }
    return res
}

Largest Number

Given a list of non negative integers, arrange them such that they form the largest number.

Example 1:

1
2
Input: [10,2]
Output: "210"

Example 2:

1
2
Input: [3,30,34,5,9]
Output: "9534330"

Note: The result may be very large, so you need to return a string instead of an integer.

Explanation

  1. If we find out the most significatn digit by using c = n / Math.pow(10, log10(n)), then it’s complicated.

  2. We can convert each integer number to string, then make a comparator to compare two string’s concatnation and sort them.

  3. Special case is if the first string starts with 0 like 00, we can return 0 as the result.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func largestNumber(nums []int) string {
    if len(nums) == 0 { return "" }
    strNums := make([]string, len(nums))
    for i := range nums {
        strNums[i] = strconv.Itoa(nums[i])
    }
    sort.Slice(strNums, func (i, j int) bool {
        return (strNums[j] + strNums[i]) < (strNums[i] + strNums[j])
    })
    if strNums[0][0] == '0' {
        return "0"
    } else {
        return strings.Join(strNums, "")
    }
}

Teemo Attacking

In LOL world, there is a hero called Teemo and his attacking can make his enemy Ashe be in poisoned condition. Now, given the Teemo’s attacking ascending time series towards Ashe and the poisoning time duration per Teemo’s attacking, you need to output the total time that Ashe is in poisoned condition.

You may assume that Teemo attacks at the very beginning of a specific time point, and makes Ashe be in poisoned condition immediately.

Example 1:

1
2
3
4
5
6
Input: [1,4], 2
Output: 4
Explanation: At time point 1, Teemo starts attacking Ashe and makes Ashe be poisoned immediately.
This poisoned status will last 2 seconds until the end of time point 2.
And at time point 4, Teemo attacks Ashe again, and causes Ashe to be in poisoned status for another 2 seconds.
So you finally need to output 4.

Example 2:

1
2
3
4
5
6
7
Input: [1,2], 2
Output: 3
Explanation: At time point 1, Teemo starts attacking Ashe and makes Ashe be poisoned.
This poisoned status will last 2 seconds until the end of time point 2.
However, at the beginning of time point 2, Teemo attacks Ashe again who is already in poisoned status.
Since the poisoned status won't add up together, though the second poisoning attack will still work at time point 2, it will stop at the end of time point 3.
So you finally need to output 3.

Note:

  1. You may assume the length of given time series array won’t exceed 10000.

  2. You may assume the numbers in the Teemo’s attacking time series and his poisoning time duration per attacking are non-negative integers, which won’t exceed 10,000,000.

Explanation

  1. We can use greedy method to solve this problem. If the difference between two adjacent time series is equals or greater than duration, we increase the result by duration. Else, we increase the result by their difference.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func findPoisonedDuration(timeSeries []int, duration int) int {
    if (len(timeSeries) == 0 || duration == 0) { return 0 }

    res := duration
    for i := 1; i < len(timeSeries); i++ {
        if timeSeries[i] - timeSeries[i-1] > duration {
            res += duration
        } else {
            res += timeSeries[i]-timeSeries[i-1]
        }
    }

    return res
}

Evaluate Division

You are given equations in the format A / B = k, where A and B are variables represented as strings, and k is a real number (floating-point number). Given some queries, return the answers. If the answer does not exist, return -1.0.

The input is always valid. You may assume that evaluating the queries will result in no division by zero and there is no contradiction.

Example 1:

1
2
3
4
5
6
Input: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
Explanation:
Given: a / b = 2.0, b / c = 3.0
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
return: [6.0, 0.5, -1.0, 1.0, -1.0 ]

Example 2:

1
2
Input: equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
Output: [3.75000,0.40000,5.00000,0.20000]

Example 3:

1
2
Input: equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
Output: [0.50000,2.00000,-1.00000,-1.00000]

Constraints:

  • 1 <= equations.length <= 20

  • equations[i].length == 2

  • 1 <= equations[i][0], equations[i][1] <= 5

  • values.length == equations.length

  • 0.0 < values[i] <= 20.0

  • 1 <= queries.length <= 20

  • queries[i].length == 2

  • 1 <= queries[i][0], queries[i][1] <= 5

  • equations[i][0], equations[i][1], queries[i][0], queries[i][1] consist of lower case English letters and digits.

Hint 1:

Do you recognize this as a graph problem?

Explanation

  1. We can solve this problem using DFS. We create a variable Map<String, HashMap<String, Double>> graph. If A/B=2.0, then we have graph[A][B] = 2.0, and graph[B][A] = 1.0/2.0. If we know A/B and B/C, then we can calculate A/C = A/B * B/C. In other words, A / C = graph[A][B] * graph[B][C].

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
func calcEquation(equations [][]string, values []float64, queries [][]string) []float64 {
    graph := make(map[string]map[string]float64)
    buildGraph(graph, equations, values)

    res := make([]float64, len(queries))
    for i := range res {
        res[i] = -1.0
    }

    for idx, query := range queries {
        a := query[0]
        b := query[1]
        if _, ok := graph[a]; !ok { continue }
        if _, ok := graph[b]; !ok { continue }
        visited := make(map[string]bool)
        helper(graph, a, b, res, idx, 1.0, visited)
    }

    return res
}

func buildGraph(graph map[string]map[string]float64, equations [][]string, values []float64) {
    for i, equation := range equations {
        a := equation[0]
        b := equation[1]
        if graph[a] == nil { graph[a] = make(map[string]float64) }
        if graph[b] == nil { graph[b] = make(map[string]float64) }
        graph[a][b] = values[i]
        graph[b][a] = 1 / values[i]
        graph[a][a] = 1.0
        graph[b][b] = 1.0
    }
}

func helper(graph map[string]map[string]float64, a string, b string, res []float64, idx int, cur float64, visited map[string]bool) {
    if _, ok := graph[a]; !ok { return }
    if visited[a] == true { return }
    visited[a] = true

    if _, ok := graph[a][b]; ok {
        res[idx] = cur * graph[a][b]
        return
    }

    for neighbor, _ := range graph[a] {
        if visited[neighbor] == true { continue }
        helper(graph, neighbor, b, res, idx, cur * graph[a][neighbor], visited)
    }
}

Subarray Product Less Than K

Your are given an array of positive integers nums.

Count and print the number of (contiguous) subarrays where the product of all the elements in the subarray is less than k.

Example 1:

1
2
3
4
Input: nums = [10, 5, 2, 6], k = 100
Output: 8
Explanation: The 8 subarrays that have product less than 100 are: [10], [5], [2], [6], [10, 5], [5, 2], [2, 6], [5, 2, 6].
Note that [10, 5, 2] is not included as the product of 100 is not strictly less than k.

Note:

  • 0 < nums.length <= 50000.

  • 0 < nums[i] < 1000.

  • 0 <= k < 10^6.

Hint 1:

For each j, let opt(j) be the smallest i so that nums[i] * nums[i+1] * … * nums[j] is less than k. opt is an increasing function.

Explanation

  1. Since this is a subarray problem, we can think of using sliding window technique or two pointers (slow, fast pointers) technique. In this problem, we will use two pointers technique.

  2. If k less than or equal to 1, we will return 0 since all elements in the input array are positive. We initialize slow = 0 and fast = 0. Loop fast from 0 to the last index of the input array, we can think of fast be the last element of the subarray, slow be the first element of the subarray. In each iteration, we calculate the production by prod *= nums[fast]. If prod < k, we can count the number of subarray be fast - slow + 1. Else, while prod >= k, we need to update prod /= nums[slow] and move slow 1 step forward.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
func numSubarrayProductLessThanK(nums []int, k int) int {
    if k <= 1 { return 0 }

    res := 0
    prod := 1
    slow := 0

    for fast := 0; fast < len(nums); fast++ {
        prod *= nums[fast]
        for prod >= k && slow <= fast {
            prod /= nums[slow]
            slow += 1
        }
        res += fast - slow + 1
    }

    return res
}

Week 5: September 29th - September 30th

Word Squares

Given a set of words (without duplicates), find all word squares you can build from them.

A sequence of words forms a valid word square if the kth row and column read the exact same string, where 0 ≤ k < max(numRows, numColumns).

For example, the word sequence ["ball","area","lead","lady"] forms a word square because each word reads the same both horizontally and vertically.

1
2
3
4
b a l l
a r e a
l e a d
l a d y

Note:

  1. There are at least 1 and at most 1000 words.

  2. All words will have the exact same length.

  3. Word length is at least 1 and at most 5.

  4. Each word contains only lowercase English alphabet a-z.

Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input:
["area","lead","wall","lady","ball"]

Output:
[
  [ "wall",
    "area",
    "lead",
    "lady"
  ],
  [ "ball",
    "area",
    "lead",
    "lady"
  ]
]

Explanation:
The output consists of two word squares. The order of output does not matter (just the order of words in each word square matters).

Example 2:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Input:
["abat","baba","atan","atal"]

Output:
[
  [ "baba",
    "abat",
    "baba",
    "atan"
  ],
  [ "baba",
    "abat",
    "baba",
    "atal"
  ]
]

Explanation:
The output consists of two word squares. The order of output does not matter (just the order of words in each word square matters).

Explanation

  1. Let’s analyze the problem’s first example. Assume the first word is b a l l, then what can the second word be? The answer is the second word must starts with a. Now, assume we have the first word and second word, then what can the third word be? The answer is the third word must starts with l e. Now, we notice that we need to quickly find a word that starts with certain characters or prefixes, the first thing pop up is using Trie. Also, this problem asks us to find different possiblities, we will use recursion to solve this kind of problem.

  2. First, we will create our Trie data structure. For the TrieNode class, in addition to the TrieNode children[], we will also have a property List<String> startWith to store a list of strings that have the same prefix.

  3. After we have our Trie setup, we need to think of how the recursion function’s signature look like. We will pass in the input String[] words, the Trie trie, the result builder List<String> cur, and the result List<List<String>> res. The basecase is if the result builder’s size is equal to the length of a word, then we can add this result builder into the result. Next, we will find the prefix from the result builder, then use the trie to get a list of words that have this prefix. Then loop through this list of words, add it to the result builder, recursively call the helper function. After the recursive function, we need to backtrack by poping the added word from the result builder.

  4. Now we have our helper function setup. In the main function, we can loop through the input String[] words. We try each word as the first word of the word squares by adding it to the result builder and call the helper function. Also remember to backtrack the added word.

Source: https://youtu.be/TdX3EgW4_eM

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
class TrieNode {
    List<String> startWith;
    TrieNode[] children;

    TrieNode() {
        startWith = new ArrayList<>();
        children = new TrieNode[26];
    }
}

class Trie {
    TrieNode root;

    Trie(String[] words) {
        root = new TrieNode();
        for (String word: words) {
            TrieNode cur = root;
            for (char ch: word.toCharArray()) {
                int chIdx = ch - 'a';
                if (cur.children[chIdx] == null) {
                    cur.children[chIdx] = new TrieNode();
                }
                cur.children[chIdx].startWith.add(word);
                cur = cur.children[chIdx];
            }
        }
    }

    List<String> findByPrefix(String prefix) {
        TrieNode cur = root;
        for (char ch: prefix.toCharArray()) {
            if (cur.children[ch - 'a'] == null) return new ArrayList<String>();
            cur = cur.children[ch - 'a'];
        }
        return cur.startWith;
    }
}

class Solution {
    void helper(String[] words, Trie trie, List<String> cur, List<List<String>> res) {
        int wordLen = words[0].length();
        int curLen = cur.size();
        if (curLen == wordLen) {
            res.add(new ArrayList<>(cur));
            return;
        }

        StringBuilder prefix = new StringBuilder();
        for (String row: cur) {
            prefix.append(row.charAt(curLen));
        }

        for (String str: trie.findByPrefix(prefix.toString())) {
            cur.add(str);
            helper(words, trie, cur, res);
            cur.remove(cur.size()-1);
        }
    }

    public List<List<String>> wordSquares(String[] words) {
        List<List<String>> res = new ArrayList<>();
        List<String> cur = new ArrayList<>();
        Trie trie = new Trie(words);

        for (String word: words) {
            cur.add(word);
            helper(words, trie, cur, res);
            cur.remove(cur.size()-1);
        }

        return res;
    }
}

Word Break

Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words.

Note:

  • The same word in the dictionary may be reused multiple times in the segmentation.

  • You may assume the dictionary does not contain duplicate words.

Example 1:

1
2
3
Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

1
2
3
4
Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
             Note that you are allowed to reuse a dictionary word.

Example 3:

1
2
Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
Output: false

Explanation

  1. We can also use dynamic programming to solve this problem. Dynamic state is a one dimensioanl array dp, and it has length dp[s.length()+1]. It’s representd if the string[0:i) can be formed by the set or not.

  2. Dynamic init is dp[0] = true because if the string is empty, then it is inside the set.

  3. Dynamic function. For example, string = "1234567", if we want to find if the string end at 5 (12345) dp[5] is inside the set, previously, we should already finish dp[0], dp[1], dp[2], dp[3], dp[4], then we can loop through these dps, so if dp[0] is true and “12345” is inside the set, then dp[5] is true; else if dp[1] is true and “2345” is inside the set then dp[5] is true; else if dp[2] is true and “345” is inside the set, then we know dp[5] is true; In other word, we are using the previous dp[j] to count whether dp[i] is true where j is from 0 to i-1.

  4. Dynamic result is the dp[dp.length()-1] which is the string from index 0 to the last character of the string.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func wordBreak(s string, wordDict []string) bool {
    set := make(map[string]bool)
    for _, word := range wordDict {
        set[word] = true
    }

    dp := make([]bool, len(s) + 1)
    dp[0] = true

    for end := 1; end <= len(s); end++ {
        for start := 0; start < end; start++ {
            if (dp[start] == true && set[s[start: end]] == true) {
                dp[end] = true
            }
        }
    }

    return dp[len(s)]
}

First Missing Positive

Given an unsorted integer array, find the smallest missing positive integer.

Example 1:

1
2
Input: [1,2,0]
Output: 3

Example 2:

1
2
Input: [3,4,-1,1]
Output: 2

Example 3:

1
2
Input: [7,8,9,11,12]
Output: 1

Follow up:

Your algorithm should run in O(n) time and uses constant extra space.

Hint 1:

Think about how you would solve the problem in non-constant space. Can you apply that logic to the existing space?

Hint 2:

We don’t care about duplicates or non-positive integers

Hint 3:

Remember that O(2n) = O(n)

Explanation

  1. If the input array length is 3, then the result can be 4 at maximum. For example:

    1
    2
    3
    4
     input = [1, 2, 3], result == 4.
 input = [1, 5, 3], result < 4.
 input = [3, 3, 3], result < 4.
 input = [-1, 3, 2], result < 4.

  2. We can also use Cyclic Sort’s swapping method to solve this problem.

  3. First start from the first number nums[i] in the array. If nums[i] is within the range between 1 to nums.length, and its value nums[i] is not equal to its corresponding index nums[i]-1’s value, in other words, if nums[i] != nums[nums[i]-1], then we swap these two elements. Else, we increase i. Repeat while i is less than nums.length.

  4. Loop from the first number to the last. If the current index is not equals to current value’s corresponding index, in other words, if nums[i]-1 != i, that means we are missing the current index’s corresponding value which is i+1.

Solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func firstMissingPositive(nums []int) int {
    i := 0
    for i < len(nums) {
        if 0 < nums[i] && nums[i] <= len(nums) && nums[i] != nums[nums[i]-1] {
            nums[i], nums[nums[i]-1] = nums[nums[i]-1], nums[i]
        } else {
            i += 1
        }
    }

    for j := 0; j < len(nums); j++ {
        if nums[j] != j + 1 { return j + 1 }
    }

    return len(nums) + 1
}